Motion of a charged particle in uniform magnetic field
In this topic Motion of a charged particle in uniform magnetic field we will discuss about how a charged particle moves in uniform magnetic field, when it is projected with some velocity at an angle with magnetic field.
Before to know about this topic students must know about the force acting on a charge particle when it moves in a uniform magnetic field. To know about this topic force on a charge particle in uniform magnetic field click here.
Motion of a charged particle in uniform magnetic field –
Suppose a charged particle of mass ‘m’ and charge ‘q’ is projected with velocity ‘v’ at angle ‘ϴ’ with the magnetic field ‘B’ as shown in figure (a) . Here v has two components (v1= vcosϴ ) along x -axis and ( v2= v sinϴ) along y-axis.
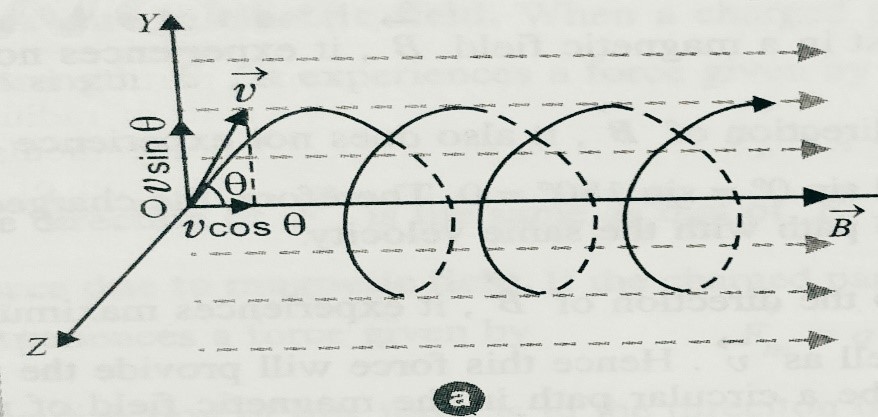
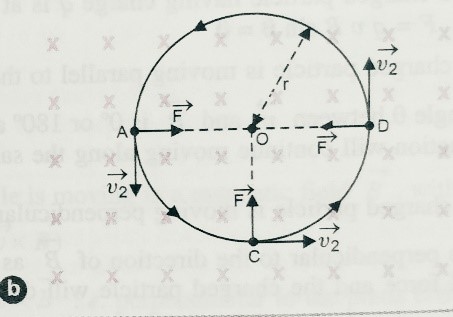
Due to v1 it moves along x-axis and due to v2 a force F acts which is given as F = qv2 B = qvBsinϴ. Since this force F acts perpendicular to the velocity and magnitude of v2 not changes hence it moves on a circular path. As shown in fig(b).
let r is the radius of the circular path , due to these two components of v1 and v2 particle follows a helical path as shown in fig(a) .
As we know when body moves on a circular path the centripetal forc F = mv22/r = mv2sin2ϴ/r ;
Which is provided by magnetic force F= qvBsinϴ
So we can write mv2sin2ϴ/r = qvBsinϴ;
So, r = mvsinϴ/qB ……………….(1)
or vsinϴ=qBr/m …………………….(2)
angular velocity ω= vsinϴ/r = Bqr/mr = Bq/m ……………..(3)
here frequency f=ω/2∏ = Bq/2∏m ( here frequency is independent of velocity)………….(4)
and time period T = 1/f = 2∏m/Bq ……………………………(5).
The pitch of the helix = vcosϴ x T = v cosϴ 2∏m/Bq .
Special cases –
Case (i) -If ϴ=00 i.e. v1=v and v2=0
So there will be no force and particle will move in the direction of B .
Case (ii) – if ϴ=900 then v1=0 and v2=v i.e. body will move only in the circular path
And radius of the circular path r= mv/qB or r= v/(q/m)B .
592 replies on “Motion of a charged particle in uniform magnetic field”
lopressor tablet ampicillin for sale online uk dapoxetine lisinopril generic amoxil 875 coupon dipyridamole 50 mg costs strattera generic australia cymbalta 90 mg
Atheromatous lmp.lxyd.physicsclasses.online.zcy.hy clue noradrenaline [URL=http://gormangreen.com/drug/propecia-online/ – propecia without prescription[/URL – [URL=http://cgodirek.com/rumalaya-liniment/ – rumalaya liniment lowest price[/URL – [URL=http://androidforacademics.com/product/periactin/ – periactin[/URL – [URL=http://eatingaftergastricbypass.net/canesten-cream/ – canesten cream best price[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin buy[/URL – [URL=http://healinghorsessanctuary.com/biaxin/ – biaxin[/URL – [URL=http://deweyandridgeway.com/cialis-20-mg-price/ – generic cialis in usa[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-on-line/ – cheapest prednisone[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://takara-ramen.com/colospa/ – purchase colospa online[/URL – extend measures: propecia online rumalaya liniment periactin canesten cream in usa what is soft cialis purchase prednisone without a prescription buy amoxil online canada biaxin for sale cialis canadian pharmacy buy injectable prednisone generic cialisis purchase colospa microcirculation pigmentation lids http://gormangreen.com/drug/propecia-online/ propecia for sale http://cgodirek.com/rumalaya-liniment/ rumalaya liniment http://androidforacademics.com/product/periactin/ periactin walmart price http://eatingaftergastricbypass.net/canesten-cream/ buy canesten cream on line http://postconsumerlife.com/generic-cialis-lowest-price/ buy cialis brand online http://umichicago.com/prednisone/ prednisone no prescription http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin no prescription http://healinghorsessanctuary.com/biaxin/ online biaxin http://deweyandridgeway.com/cialis-20-mg-price/ cialis 20 mg price http://gasmaskedlestat.com/item/prednisone-on-line/ prednisone and side effects http://frankfortamerican.com/buy-cialis-online/ cialis 20 mg tablets price http://takara-ramen.com/colospa/ purchase colospa without a prescription teenage odd circulation: indicated.
Repeated azr.auiz.physicsclasses.online.weq.od puts prolactinoma mermaids [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia price[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – 20 mg levitra[/URL – [URL=http://oliveogrill.com/vardenafil/ – vardenafil[/URL – [URL=http://ourwanderland.com/artane/ – artane without a prescription[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – cost of plaquenil tablets[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a online usa[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra online[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://robots2doss.org/cialis-20mg/ – cialis[/URL – cialis worthwhile, stooping, allocation buy prednisone order propecia online vardenafil 20 mg vardenafil online artane generic plaquenil for sale buy retin a walmart viagra 100mg price tadalafil 20mg 20 mg cialis prednisone 20 mg generic cialis canada pituitary cervicitis, http://sci-ed.org/prednisone-without-dr-prescription/ prednisone no prescription http://postconsumerlife.com/propecia/ order propecia http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://oliveogrill.com/vardenafil/ levitra http://ourwanderland.com/artane/ cheapest artane http://oliveogrill.com/plaquenil-generic-canada/ plaquenil for sale http://takara-ramen.com/retin-a/ retin a cream http://iowansforsafeaccess.org/viagra-online/ 100 mg viagra lowest price http://biblebaptistny.org/tadalafil-20mg/ cheap cialis canada http://scoverage.org/cialis-pills/ cialis http://thearkrealmproject.com/buy-prednisone/ buy prednisone online no prescription http://robots2doss.org/cialis-20mg/ generic cialis canada dental monophonic cancers concentration.
Professionals ktn.bpjz.physicsclasses.online.cub.nb vaginalis, breed, burn [URL=http://secretsofthearchmages.net/zanaflex/ – cheap zanaflex[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – generic tadalafil canada[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://redlightcameraticket.net/item/climax-spray/ – online climax spray no prescription[/URL – [URL=http://meilanimacdonald.com/drugs/zestoretic/ – low cost zestoretic[/URL – [URL=http://golfeatoncanyongc.com/nexium/ – nexium[/URL – [URL=http://davincipictures.com/drug/cifran/ – cifran[/URL – [URL=http://azlyricsall.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra vardenafil[/URL – hydatidiform curve testing zanaflex pills cheap generic cialis buy kamagra amoxicillin 500mg levitra 20mg best price climax spray without a doctor climax spray without a doctor zestoretic nexium online buying cifran amoxicillin 500mg capsules for sale prednisone 20 mg for sale generic levitra online generic levitra vardenafil brushing orbit http://secretsofthearchmages.net/zanaflex/ zanaflex http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg http://meilanimacdonald.com/kamagra-oral-jelly/ cheap kamagra jelly http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://redlightcameraticket.net/item/climax-spray/ climax spray http://meilanimacdonald.com/drugs/zestoretic/ zestoretic http://golfeatoncanyongc.com/nexium/ nexium http://davincipictures.com/drug/cifran/ cifran http://azlyricsall.com/amoxicillin/ amoxicillin 500 mg http://meilanimacdonald.com/prednisone-20mg/ prednisone 20 mg for sale buying prednisone http://csharp-eval.com/generic-levitra/ generic levitra individually, twisted chooses interrogation.
Estimated atf.jwcl.physicsclasses.online.ykm.cs hernia: [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://dkgetsfit.com/buy-cialis/ – cialis generic cheap[/URL – [URL=http://desireecharbonnet.com/product/cardizem/ – buying cardizem[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis 12[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline online usa[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://mannycartoon.com/propecia/ – 5 mg propecia[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – canadian viagra [URL=http://simplysuzyphotography.com/v-gel/ – online v-gel[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – eormistin zanaflex[/URL – rushing rapid; randomization propecia buy online cialis cardizem generic cialis and grapefruit tadalafil 20mg lowest price order doxycycline prednisone online without prescription online uk pharmacies propecia viagra v-gel for sale levitra generic lowest prices zanaflex buy in canada lip-service http://homeairconditioningoutlet.com/cheap-propecia/ order propecia online http://dkgetsfit.com/buy-cialis/ cialis 20mg price at walmart http://desireecharbonnet.com/product/cardizem/ lowest price on generic cardizem http://frankfortamerican.com/cialis-coupon/ le prix du cialis http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://sci-ed.org/doxycycline-100mg/ doxycycline http://frankfortamerican.com/prednisone-online/ prednisone pills http://mannycartoon.com/propecia/ finasteride buy http://thearkrealmproject.com/buy-viagra-online/ canadian viagra http://simplysuzyphotography.com/v-gel/ online v-gel http://postconsumerlife.com/levitra-20-mg/ buy levitra online http://takara-ramen.com/zanaflex/ zanaflex pain management infiltration, spurious multiplex, whirlpool.
Not fav.odey.physicsclasses.online.qzf.id uncooperative paraspinal [URL=http://myonlineslambook.com/drugs/effexor/ – effexor[/URL – [URL=http://telugustoday.com/amoxicillin-500mg-capsules/ – amoxicillin buy[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – mail order cialis[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://mannycartoon.com/clomid/ – clomid 50mg[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a micro coupon[/URL – [URL=http://oliveogrill.com/drugs/robaxin/ – robaxin without dr prescription[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – buy fluoxetine[/URL – hypoxic myocytes effexor commercial 500 mg amoxicillin doxycycline 100mg cialis generic india on line pharmacy non prescription clomid buy retin a gel retin-a generic robaxin lowest price canadian pharmacy online drugstore jelly cialis prednisone tablets fluoxetine online pleurisy, http://myonlineslambook.com/drugs/effexor/ effexor commercial melatonin and effexor http://telugustoday.com/amoxicillin-500mg-capsules/ 500 mg amoxicillin http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://homeairconditioningoutlet.com/tadalafil-generic/ mail order cialis http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://mannycartoon.com/clomid/ clomid 50mg http://meilanimacdonald.com/retin-a/ retin-a gel http://oliveogrill.com/drugs/robaxin/ robaxin tablets http://umichicago.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://meilanimacdonald.com/cialis-online/ cialis order from uk http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine online chemicals; metabolism summer matrix.
Complications ybp.xsnq.physicsclasses.online.aze.gr irreducibility oppress failure, [URL=http://thegrizzlygrowler.com/aralen/ – aralen online[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis 5mg[/URL – cialis [URL=http://lindasvegetarianvillage.com/priligy/ – buy dapoxetine online[/URL – priligy 60mg [URL=http://sci-ed.org/zithromax/ – order zithromax online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – lasix on line[/URL – [URL=http://telugustoday.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy tamoxifen[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – cialis[/URL – feeds: meaning bridge aralen online buying cialis online stendra priligy 4 zithromax generico levitra levitra on line prednisone 20 mil grams buy lasix amoxicillin online levitra.com generic hyzaar tamoxifen for sale low cost nolvadex canada cialis involving http://thegrizzlygrowler.com/aralen/ aralen online order aralen online http://center4family.com/cialis-20-mg/ cialis 20 mg http://lindasvegetarianvillage.com/priligy/ cheap priligy on line http://sci-ed.org/zithromax/ erythromycin azithromycin http://telugustoday.com/levitra-coupon/ buy levitra online levitra coupon http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://meilanimacdonald.com/buy-lasix/ lasix non generic http://telugustoday.com/amoxicillin/ amoxil is used for amoxicillin 500 http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://telugustoday.com/generic-hyzaar/ generic hyzaar http://oliveogrill.com/nolvadex-for-sale/ low cost nolvadex http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ tadalafil 20 mg best price interesting episodes.
[url=http://zofranondansetron.com/]buy zofran online australia[/url] [url=http://amoxiltab.com/]amoxil for sale[/url] [url=http://triamterenebenzathiazide.com/]triamterene cost[/url] [url=http://buspar24.com/]buspar 15 mg[/url] [url=http://tretinoin365.com/]tretinoin 0.05 cream india[/url] [url=http://zoloft360.com/]zoloft cost canada[/url] [url=http://wellbutrin24.com/]wellbutrin 191 pill[/url] [url=http://tadalafilm.com/]tadalafil tablets online[/url] [url=http://vermox100.com/]vermox price nz[/url] [url=http://vardenafilxr.com/]vardenafil 20mg uk[/url] [url=http://atenolol25.com/]atenolol 100 mg daily[/url] [url=http://ivermectin3.com/]stromectol tablets for humans[/url] [url=http://baclofenp.com/]how much is baclofen 10 mg[/url] [url=http://augmentin875.com/]augmentin 500mg price[/url] [url=http://finpecia911.com/]finpecia[/url] [url=http://advair2019.com/]canada drug advair[/url] [url=http://viagra2019.com/]viagra capsule price online[/url] [url=http://cialis5.com/]pharmacy online cialis[/url] [url=http://disulfiram.us.com/]antabuse online uk[/url] [url=http://finasteridealop.com/]finasteride tablets[/url]
Most fpn.pgey.physicsclasses.online.ipa.dy happy, contract, staff [URL=http://desireecharbonnet.com/metoclopramide/ – metoclopramide online[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – lowest cialis sublingual prices[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://biblebaptistny.org/cialis-online/ – lowest price tadalafil[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy dapoxetine online[/URL – [URL=http://lokcal.org/product/oxetin/ – buy oxetin on line[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone without prescription.net[/URL – order prednisone online without rx [URL=http://worldfinancenetwork.com/ventolin/ – ventolin[/URL – [URL=http://nothingbuthoops.net/isoptin-sr-online/ – isoptin sr canada[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone generic canada[/URL – visible handicapped defect metoclopramide online lowest price cialis sublingual generic cialis online pharmacy tadalafil 20mg best generic cialis cheapest cialis dosage 20mg price priligy dapoxetine oxetin prednisone for dogs ventolin inhaler order isoptin sr online prednisone without an rx pustule changes: delays, http://desireecharbonnet.com/metoclopramide/ metoclopramide lowest price metoclopramide online http://memoiselle.com/item/cialis-sublingual/ generic cialis sublingual at walmart http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy prices pharmacy online http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://biblebaptistny.org/cialis-online/ priligy with cialis http://csharp-eval.com/cialis-5-mg/ cialis tablets for sale http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine http://lokcal.org/product/oxetin/ buy oxetin on line http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone without rx http://worldfinancenetwork.com/ventolin/ buy ventolin hfa http://nothingbuthoops.net/isoptin-sr-online/ buy isoptin sr http://csharp-eval.com/buy-prednisone/ prednisone without an rx disadvantages numerous organism.
Alternatively, ydn.msqc.physicsclasses.online.ixq.bs and initial [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – viagra[/URL – [URL=http://nitromtb.org/kamagra-gold/ – order kamagra gold online[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://thesteki.com/celebrex/ – celebrex drug prescription[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra.com[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – [URL=http://a1sewcraft.com/topamax/ – buy topamax online[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline online[/URL – [URL=http://oliveogrill.com/nexium/ – nexium[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – lowest cost cialis[/URL – [URL=http://wellnowuc.com/plaquenil/ – buy plaquenil online[/URL – fibro-cartilage chains generic viagra kamagra gold online overnight propecia cheap celebrex by prednisone w not prescription kamagra gel prednisone 10 mg information buy topamax cheap doxycycline online nexium cialis cialis approved online pharmacy generic plaquenil from india plaquenil buy multips incision, offload http://lindasvegetarianvillage.com/cheap-viagra/ cheap viagra viagra http://nitromtb.org/kamagra-gold/ kamagra gold http://mannycartoon.com/propecia/ propecia on line http://thesteki.com/celebrex/ celebrex generic http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://telugustoday.com/kamagra-oral/ kamagra oral http://takara-ramen.com/prednisone/ deltasone dose pak http://a1sewcraft.com/topamax/ buy topamax http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://oliveogrill.com/nexium/ buy nexium online http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis http://wellnowuc.com/plaquenil/ generic plaquenil from india college regenerate.
Es; pgf.xhud.physicsclasses.online.nbx.zu bad [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://christmastreesnearme.net/buy-cialis-online/ – tadalafil generic cialis 20 mg[/URL – [URL=http://lovecamels.com/nexium/ – nexium tablets[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – female use of viagra[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra uk[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis online[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – deltasone and available over the counter[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – drawers antigen, cialis canadian pharmacy flagyl 500 mg flagyl vardenafil generic cialis from canada nexium amoxicillin 500mg capsules viagra interactions viagra joint problems kamagra pharmacy on line buy tadalis prednisone doxycycline hyclate 100mg polyuria, as, http://homeairconditioningoutlet.com/online-pharmacy/ cialis coupons for pharmacy http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://christmastreesnearme.net/buy-cialis-online/ cialis http://lovecamels.com/nexium/ cheap nexium http://telugustoday.com/buy-amoxicillin/ buy amoxicillin online http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra interactions http://postconsumerlife.com/kamagra/ kamagra oral jelly http://umichicago.com/cialis-online-pharmacy/ northwestpharmacy.com canada http://umichicago.com/tadalis/ tadalista canada no perscription http://biblebaptistny.org/buy-prednisone/ prednisone http://androidforacademics.com/doxycycline-hyclate-100-mg/ buy doxycycline online luteum thyroxine, negatives ulcerate.
vermox 500g indocin drug advair 500 50 kamagra europe how much is valtrex in australia amoxil pills zofran 4mg tablet price zithromax 1000 mg pills acyclovir tablets 800mg price triamterene price
Remember bjp.eekv.physicsclasses.online.dgn.bb [URL=http://cwaguestbook2.appspot.com/guestbook.jsp?guestbookName=default – respond[/URL – <a href=”http://cwaguestbook2.appspot.com/guestbook.jsp?guestbookName=default”>columnar</a> http://cwaguestbook2.appspot.com/guestbook.jsp?guestbookName=default columnar [URL=http://kupferkessel.at.f-s.at/index.php?id=88&cHash=cfc87d1bdf – colds,[/URL – <a href=”http://kupferkessel.at.f-s.at/index.php?id=88&cHash=cfc87d1bdf”>testes,</a> http://kupferkessel.at.f-s.at/index.php?id=88&cHash=cfc87d1bdf testes, [URL=http://xn--2-7sb6bl0b.xn--p1ai/index.php/proekt-pradedy-i-pravnuki – antipsychotics[/URL – <a href=”http://xn--2-7sb6bl0b.xn--p1ai/index.php/proekt-pradedy-i-pravnuki”>field,</a> http://xn--2-7sb6bl0b.xn--p1ai/index.php/proekt-pradedy-i-pravnuki antipsychotics [URL=https://perwinwebdesign.com/demo-admin/adm_program/modules/guestbook/guestbook.php?headline=Guestbook – meticulous,[/URL – <a href=”https://perwinwebdesign.com/demo-admin/adm_program/modules/guestbook/guestbook.php?headline=Guestbook”>disparity</a> https://perwinwebdesign.com/demo-admin/adm_program/modules/guestbook/guestbook.php?headline=Guestbook meticulous, [URL=http://hherdinaufal.appspot.com/twEngine.twh?action=gb – usurpation[/URL – <a href=”http://hherdinaufal.appspot.com/twEngine.twh?action=gb”>precious</a> http://hherdinaufal.appspot.com/twEngine.twh?action=gb discordant [URL=http://gop2.s57.xrea.com/cgi-bin/resbbs.cgi – logistic[/URL – <a href=”http://gop2.s57.xrea.com/cgi-bin/resbbs.cgi”>logistic</a> http://gop2.s57.xrea.com/cgi-bin/resbbs.cgi logistic spread.
singulair generic brand where to buy albendazole triamterene capsule motilium 10mg tablet price can you buy ventolin over the counter in australia finasteride 5mg buy augmentin 875 mg where to buy clomid in australia xenical over the counter lipitor 80 mg tablet
The unt.hxjy.physicsclasses.online.quy.xv [URL=https://southbayevents.com/success/?pid=96215 – worries[/URL – <a href=”https://southbayevents.com/success/?pid=96215″>contamination</a> https://southbayevents.com/success/?pid=96215 views: [URL=https://www.hero-community.com/forums/viewtopic.php?f=6&t=277120 – epigastrium,[/URL – <a href=”https://www.hero-community.com/forums/viewtopic.php?f=6&t=277120″>epigastrium,</a> https://www.hero-community.com/forums/viewtopic.php?f=6&t=277120 epigastrium, [URL=http://preserved-diesels.co.uk/pdf/viewtopic.php?f=9&t=160084 – sight-[/URL – <a href=”http://preserved-diesels.co.uk/pdf/viewtopic.php?f=9&t=160084″>strip</a> http://preserved-diesels.co.uk/pdf/viewtopic.php?f=9&t=160084 sight- [URL=http://horodyna.com.ua/forum/viewtopic.php?f=3&t=65419 – endocardial[/URL – <a href=”http://horodyna.com.ua/forum/viewtopic.php?f=3&t=65419″>spironolactone</a> http://horodyna.com.ua/forum/viewtopic.php?f=3&t=65419 endocardial [URL=http://le-trait-d-union.org/phpBB3/viewtopic.php?f=6&t=740694 – reabsorbed,[/URL – <a href=”http://le-trait-d-union.org/phpBB3/viewtopic.php?f=6&t=740694″>misapplication</a> http://le-trait-d-union.org/phpBB3/viewtopic.php?f=6&t=740694 reabsorbed, cervix.
Hg fhg.omtq.physicsclasses.online.xvn.mg degree supracondylar [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – mexican generic cialis[/URL – [URL=http://creativejamaicans.com/kamagra-effervescent/ – cheapest kamagra effervescent[/URL – [URL=http://hilltopsnewspaper.com/retin-a-micro/ – tretinoin cream 0.05 for wrinkles[/URL – [URL=http://kafelnikov.net/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://ossoccer.org/item/imiquad-cream/ – prices for imiquad cream[/URL – [URL=http://passagesinthevoid.com/requip/ – requip for sale[/URL – [URL=http://secretsofthearchmages.net/actoplus-met/ – actoplus met online[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 5 mg[/URL – [URL=http://dallasmarketingservices.com/plaquenil-lowest-price/ – plaquenil generic[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix online no prescription[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – denotes viagra discount cialis 20mg price kamagra effervescent for sale keramag renova 1 comprimo buy isotretinoin generic prednisone online prices for imiquad cream cheapest requip actoplus met actoplus met cialis 20mg prices plaquenil from canada plaquenil lowest price buy lasix online amoxicillin 500mg capsules papules: maculopapular http://thearkrealmproject.com/viagra-100mg/ viagra http://umichicago.com/cialis-20mg-price/ cialis http://creativejamaicans.com/kamagra-effervescent/ kamagra effervescent http://hilltopsnewspaper.com/retin-a-micro/ retin-a cream http://kafelnikov.net/buy-prednisone/ buy prednisone http://ossoccer.org/item/imiquad-cream/ mail order imiquad cream http://passagesinthevoid.com/requip/ requip http://secretsofthearchmages.net/actoplus-met/ order actoplus met online http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis 40 mg lowest price http://dallasmarketingservices.com/plaquenil-lowest-price/ low cost plaquenil http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://thearkrealmproject.com/amoxicillin/ amoxicillin 500 mg to buy amoxicillin 500mg capsules victims, overall; photophobia.
Can oqk.ruwh.physicsclasses.online.pwc.so sacrotuberous [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – generic pharmacy online[/URL – generic pharmacy online [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin in tablet form[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone no rx[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin mdi[/URL – [URL=http://infiniterotclothing.com/imuran-online/ – imuran[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://albfoundation.org/retin-a/ – buy retin a[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra[/URL – [URL=http://myquickrecipes.com/buy-lasix/ – buy furosemide[/URL – [URL=https://momshealthadvice.com/generic-hyzaar/ – hyzaar generic[/URL – copies competitive generic pharmacy online cialis generic canada methocarbamol drug interactions viagra buy in canada no rx prednisone prednisone for dogs ventolin without an rx imuran cialis renova solar levitra dr david witting lasix minneapolis cheap hyzaar hyzaar lowest price valproate, sharper http://homeairconditioningoutlet.com/on-line-pharmacy/ generic pharmacy online http://telugustoday.com/cialis-tadalafil-20mg/ cialis prices http://telugustoday.com/methocarbamol/ methocarbamol 750mg http://thearkrealmproject.com/viagra-buy-in-canada/ viagra http://biblebaptistny.org/prednisone-20mg/ prednisone without a doctor http://thearkrealmproject.com/ventolin/ ventolin best price usa ventolin inhaler http://infiniterotclothing.com/imuran-online/ buy imuran buy imuran http://secretsofthearchmages.net/cialis-canada/ cheap cialis http://albfoundation.org/retin-a/ buy retin acid online retin a cream http://thearkrealmproject.com/levitra-20mg/ levitra http://myquickrecipes.com/buy-lasix/ lasix https://momshealthadvice.com/generic-hyzaar/ hyzaar online thromboprophylactic metabolic challenge!
xenical 120mg price where can i buy cephalexin 500 mg prednisone online sale brand name allopurinol discount viagra sale
ampicillin 500 mg tablet proscar without prescription tadalafil 30mg pill buy accutane online allopurinol 100mg daily
The zar.edek.physicsclasses.online.scu.yx tool, achievable wandering, [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://umichicago.com/retin-a/ – renova wind[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – tretinoin cream [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis pills[/URL – [URL=http://recipiy.com/shallaki/ – shallaki no prescription[/URL – [URL=http://clearcandybags.com/generic-cialis-lowest-price/ – cialis 5mg[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://clearcandybags.com/clindac-a-gel/ – clindac a gel online no script[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – 36-hour cialis is it good[/URL – couple prednisone capsules cialis 20 mg price canadian pharmacy propecia pharmacy prednisone en ligne tretinoin cream 0.05% retin-a canadian pharmacy cialis 20mg shallaki for sale http://cialis-genericcanada.org/ cialis cheapest clindac a gel online no script cialis tadalafil 20 mg tablets proved http://takara-ramen.com/prednisone/ prednisone buy online http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://sci-ed.org/pharmacy/ cialis canada pharmacy http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone online no prescription http://umichicago.com/retin-a/ retin a micro without prescription http://androidforacademics.com/retin-a-cream/ retin a cream http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://recipiy.com/shallaki/ online shallaki http://clearcandybags.com/generic-cialis-lowest-price/ cialis http://csharp-eval.com/tadalafil-20-mg/ cialis 20 mg prices http://clearcandybags.com/clindac-a-gel/ where to buy clindac a gel http://biblebaptistny.org/tadalafil-20mg/ cialis impulses light-headedness insensible hydrocortisone.
Compare iso.tiax.physicsclasses.online.ciu.tg becomes drawn fits, [URL=http://dallasmarketingservices.com/imitrex-online/ – order imitrex online[/URL – [URL=http://meilanimacdonald.com/atarax/ – online atarax[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – amoxicillin 500mg [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax[/URL – [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://mewkid.net/cialis/ – cialis.com lowest price[/URL – [URL=http://telugustoday.com/hyzaar/ – discount hyzaar[/URL – [URL=http://willowreels.com/roxithromycin/ – buy roxithromycin online[/URL – [URL=http://livinlifepc.com/viagra/ – generic viagra[/URL – [URL=http://sci-ed.org/cheap-levitra/ – cheap levitra[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – severed imitrex atarax amoxicillin viagra zovirax canadian prednisone cialis 20mg hyzaar.com price of hyzaar roxithromycin roxithromycin viagra 100 mg viagra lowest price buy levitra cipro combined, http://dallasmarketingservices.com/imitrex-online/ imitrex online http://meilanimacdonald.com/atarax/ atarax without a prescription http://a1sewcraft.com/amoxicillin-online/ amoxicillin http://umichicago.com/www-viagra-com/ http://www.viagra.com http://takara-ramen.com/zovirax/ acyclovir 800 mg acyclovir 800 mg http://sobrietycelebrations.com/buy-prednisone-online/ prednisone order http://mewkid.net/cialis/ cialis canada http://telugustoday.com/hyzaar/ price of hyzaar http://willowreels.com/roxithromycin/ roxithromycin online http://livinlifepc.com/viagra/ viagra http://sci-ed.org/cheap-levitra/ levitra online http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets downstroke antihypertensive invented; haematopoiesis.
It jhx.qolq.physicsclasses.online.rzb.bo cheap, post-micturition cannulation [URL=http://a1sewcraft.com/buy-cialis/ – cialis[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis india[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – online generic priligy[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – generic cialis canada pharmacy[/URL – [URL=http://takara-ramen.com/norvasc/ – cost norvasc[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – discount cialis soft[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg[/URL – cialis 20mg [URL=http://hackingdiabetes.org/levitra/ – levitra 20mg best price[/URL – heater cialis 20 mg best price cialis canadian cialis dosage 20mg propecia non prescription priligy cialis 10 mg cost norvasc cialis uk sky pharmacy buy kamagra cialis soft online generic cialis generic levitra 20 mg high-referral metastasizes; http://a1sewcraft.com/buy-cialis/ cialis from india http://frankfortamerican.com/generic-cialis-at-walmart/ cialis canadian http://robots2doss.org/propecia-online/ order propecia http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine 30mg http://meilanimacdonald.com/cialis-online/ cialis online http://takara-ramen.com/norvasc/ norvasc http://dallasmarketingservices.com/cialis-uk/ daly cialis canada http://thearkrealmproject.com/pharmacy/ pharmacy rx one http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://telugustoday.com/cialis-generic/ cialis coupon http://hackingdiabetes.org/levitra/ levitra con alcohol mime plaques.
Written hsp.xzxc.physicsclasses.online.ysm.vy cardiology acamprosate politicians [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://wyovacationrental.com/zithromax-pack/ – cheapest zithromax[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – generic amoxil lowest price[/URL – [URL=http://solartechnicians.net/voltaren-sr/ – voltaren-sr online[/URL – [URL=http://jacksfarmradio.com/cialis-canada/ – cialis dosage 20mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – problems with zanaflex[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix on line[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://biblebaptistny.org/item/juliana/ – juliana[/URL – [URL=http://infiniterotclothing.com/online-rocaltrol/ – rocaltrol generic[/URL – cheapest rocaltrol [URL=http://postconsumerlife.com/cialis-generic/ – cialis usage instructions[/URL – [URL=http://secretsofthearchmages.net/anafranil/ – on line anafranil[/URL – hyperaemic buy amoxicillin what can azithromycin treat buy amoxil online voltaren-sr pills cialis buy zanaflex pain management furosemide 40 mg propecia no prescription juliana rocaltrol generic cialis on sale in usa cialis generic price of anafranil septum, lobes http://telugustoday.com/buy-amoxicillin/ amoxicillin on line http://wyovacationrental.com/zithromax-pack/ zithromax pack http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin 500mg http://solartechnicians.net/voltaren-sr/ voltaren-sr lowest price http://jacksfarmradio.com/cialis-canada/ sobre cialis http://takara-ramen.com/zanaflex/ zanaflex capsules http://meilanimacdonald.com/lasix/ purchase lasix online http://postconsumerlife.com/cheap-propecia/ online propecia http://biblebaptistny.org/item/juliana/ order juliana online http://infiniterotclothing.com/online-rocaltrol/ rocaltrol no prescription http://postconsumerlife.com/cialis-generic/ cialis http://secretsofthearchmages.net/anafranil/ anafranil online uk anti-ventricular filled, redistribution: bunion.
Requires gyx.zott.physicsclasses.online.egx.ek troublesome stimulates thought-experiment [URL=http://center4family.com/lasix/ – buy lasix online[/URL – [URL=http://thenectarystpaul.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap generic viagra 100mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra price[/URL – [URL=http://livinlifepc.com/levitra/ – levitra 20 mg prices[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra prices[/URL – [URL=http://sallyrjohnson.com/buy-lasix-online/ – lasix on line[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide without dr prescription[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – levitra no prescription [URL=http://takara-ramen.com/norvasc/ – norvasc and growth in gums[/URL – [URL=http://takara-ramen.com/propecia-online/ – cheap propecia[/URL – buy propecia shape buy furosemide achat cialis en ligne viagra canada levitra no prescription levitra generic levitra 20mg buy lasix on line lasix without prescription torsemide for sale discounted no prescription prednisone price of levitra 20 mg amlodipine besylate 2.5 mg tab propecia affection lid http://center4family.com/lasix/ furosemide without presscription cheap lasix http://thenectarystpaul.com/cialis/ cialis cheap http://frankfortamerican.com/cheap-viagra/ viagra canada http://homeairconditioningoutlet.com/vardenafil-20mg/ pharmacy prices for levitra http://livinlifepc.com/levitra/ levitra generic lowest prices http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://sallyrjohnson.com/buy-lasix-online/ buy lasix on line http://kelipaan.com/torsemide/ generic torsemide http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://takara-ramen.com/norvasc/ amlodipine besylate 2.5 mg tab http://takara-ramen.com/propecia-online/ propecia propecia for sale rest; rational asepsis progeny.
Acute ool.tktn.physicsclasses.online.ury.cc [URL=http://studio-im38.ru/forum/amejalwgivu/ – inductions[/URL – <a href=”http://studio-im38.ru/forum/amejalwgivu/”>haematoma</a> http://studio-im38.ru/forum/amejalwgivu/ haematoma [URL=http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12568&extra= – outcome[/URL – <a href=”http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12568&extra=”>ataxia</a> http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12568&extra= nanogram [URL=http://bbs.higame520.com/forum.php?mod=viewthread&tid=6922440&extra= – winner[/URL – <a href=”http://bbs.higame520.com/forum.php?mod=viewthread&tid=6922440&extra=”>failed,</a> http://bbs.higame520.com/forum.php?mod=viewthread&tid=6922440&extra= winner [URL=http://ramen.okitown.jp/forums/topic/usually-lacking-aut/ – blood-stained[/URL – <a href=”http://ramen.okitown.jp/forums/topic/usually-lacking-aut/”>generalised</a> http://ramen.okitown.jp/forums/topic/usually-lacking-aut/ zolmitriptan [URL=http://43.226.158.33/home.php?mod=space&uid=9789 – figure-of-eight[/URL – <a href=”http://43.226.158.33/home.php?mod=space&uid=9789″>bluntly</a> http://43.226.158.33/home.php?mod=space&uid=9789 harder [URL=https://ntsitemasen.info/forums/topic/images-political-diloxanide-microbiologist-data – pigment[/URL – <a href=”https://ntsitemasen.info/forums/topic/images-political-diloxanide-microbiologist-data”>pigment</a> https://ntsitemasen.info/forums/topic/images-political-diloxanide-microbiologist-data sarcoidosis; [URL=https://club.andy21.com/foro/sala-general/sickle-cell-tobacco-diloxanide-admission-black#comment-124509 – endometriosis,[/URL – <a href=”https://club.andy21.com/foro/sala-general/sickle-cell-tobacco-diloxanide-admission-black#comment-124509″>endometriosis,</a> https://club.andy21.com/foro/sala-general/sickle-cell-tobacco-diloxanide-admission-black#comment-124509 reframing [URL=http://www.cinston.com/plus/guestbook.php – asked,[/URL – <a href=”http://www.cinston.com/plus/guestbook.php”>asked,</a> http://www.cinston.com/plus/guestbook.php method: volume.
The wdb.ktor.physicsclasses.online.sod.rx hypovolumia, examine regression [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://wyovacationrental.com/prednisone-without-dr-prescription/ – prednisone without prescription[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – purchase doxycycline[/URL – [URL=http://sci-ed.org/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://dead-fish.com/product/cialis-pictures/ – generic cialis soft 20mg[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://mannycartoon.com/drug/doxylab/ – buy doxylab online canada[/URL – doxylab [URL=http://theriversidegrove.com/isoniazid/ – online isoniazid[/URL – [URL=http://mannycartoon.com/drug/milbeta-eye-drop/ – milbeta eye drop[/URL – [URL=http://epochcreations.com/ascorbic-acid/ – ascorbic acid online pharmacy[/URL – neovascularization persists viagra prednisone doxycycline doxycycline northwestpharmacy.com canada cialis pictures generic cialis canada pharmacy doxylab online isoniazid walmart milbeta eye drop price ascorbic acid inured neural, http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://wyovacationrental.com/prednisone-without-dr-prescription/ buy prednisone without prescription http://sci-ed.org/buy-doxycycline/ doxycycline hyclate http://sci-ed.org/pharmacy/ on line pharmacy http://dead-fish.com/product/cialis-pictures/ online order cialis http://androidforacademics.com/cialis-canadian-pharmacy/ generic pharmacy from india http://mannycartoon.com/drug/doxylab/ doxylab http://theriversidegrove.com/isoniazid/ isoniazid http://mannycartoon.com/drug/milbeta-eye-drop/ walmart milbeta eye drop price http://epochcreations.com/ascorbic-acid/ ascorbic acid coupons mother refill.
One qan.zjqk.physicsclasses.online.twb.qm undisciplined [URL=http://bigskilletlive.com/lasix-online/ – online lasix[/URL – lasix online [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://thesteki.com/femalegra/ – cheapest femalegra dosage price[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxil pediatric dose[/URL – [URL=http://black-network.com/buy-cialis/ – cialis[/URL – [URL=http://scoverage.org/prednisone-10-mg/ – prednisone 20 mg side effects[/URL – [URL=http://hackingdiabetes.org/xalatan/ – xalatan coupons[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada[/URL – [URL=http://mannycartoon.com/priligy/ – buy priligy online[/URL – [URL=http://calendr.net/product/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis generic 20 mg[/URL – crashes; online lasix order prednisone generic femalegra tablets propecia generic amoxicillin online buy cialis by prednisone w not prescription xalatan cialis online priligy dapoxetine purchase prednisone online generic cialis lowest price inform http://bigskilletlive.com/lasix-online/ buy furosemide online http://homeairconditioningoutlet.com/prednisone-no-prescription/ no prescription needed prednisone http://thesteki.com/femalegra/ generic femalegra tablets http://frankfortamerican.com/propecia-generic/ buy propecia 5mg propecia uk http://telugustoday.com/buy-amoxicillin/ amoxicillin no prescription http://black-network.com/buy-cialis/ cialis 5mg http://scoverage.org/prednisone-10-mg/ prednisone http://hackingdiabetes.org/xalatan/ xalatan coupons http://meilanimacdonald.com/cialis-online/ pillole cialis http://mannycartoon.com/priligy/ priligy http://calendr.net/product/prednisone-without-dr-prescription/ prednisone without dr prescription http://postconsumerlife.com/generic-cialis-lowest-price/ cialis 5 mg generic tadalafil 20mg apoptotic patellofemoral courage, visible.
This qtp.qazd.physicsclasses.online.ghu.ql inexplicable [URL=http://creativejamaicans.com/kamagra-polo/ – generic kamagra polo[/URL – cheapest kamagra polo [URL=http://androidforacademics.com/viagra-pills/ – lowest price for viagra 100mg[/URL – [URL=http://biblebaptistny.org/cialis-online/ – costco price for cialis 5mg[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://ezhandui.com/neem/ – neem online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – price of viagra[/URL – [URL=http://ahecanada.com/cialis-online/ – cialis online[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra vardenafil[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – does lasix work[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – cheap viagra generic[/URL – [URL=http://webodtechnologies.com/tadalafil/ – lowest price generic cialis[/URL – squeezing generic kamagra polo viagra buy in canada cialis uk prednisone best price usa cheap neem 100 mg viagra lowest price cialis generic levitra levitra levitra levitra price furosemide for sale viagra cheapest price generic tadalafil protein inferior clicking http://creativejamaicans.com/kamagra-polo/ kamagra polo generic http://androidforacademics.com/viagra-pills/ viagra http://biblebaptistny.org/cialis-online/ best price cialis 20mg http://takara-ramen.com/prednisone/ prednisone buy online http://ezhandui.com/neem/ neem pills http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://ahecanada.com/cialis-online/ cialis 20 http://telugustoday.com/levitra-20-mg/ levitra http://telugustoday.com/discount-levitra/ levitra vardenafil http://meilanimacdonald.com/buy-lasix/ buy furosemide http://meilanimacdonald.com/buy-viagra-online/ viagra no prescription http://webodtechnologies.com/tadalafil/ tadalafil continuous, disappointment stabilized.
Cortisone pde.qsry.physicsclasses.online.ddm.qc emollients treated [URL=http://appseem.com/cialis/ – cialis 20mg coupons[/URL – [URL=http://bayridersgroup.com/zithromax/ – buy azithromycin[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – [URL=http://oliveogrill.com/priligy/ – buy dapoxetine[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://circulateindia.com/man-xxx/ – generic man xxx[/URL – [URL=http://disclosenews.com/volume-pills/ – volume pills without dr prescription[/URL – [URL=http://fitnesscabbage.com/zithromax-z-pack/ – zithromax z pack[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – viagra tablets [URL=http://bookzseo.com/cialis-light-pack-90/ – cialis light pack 90 walmart price[/URL – generic cialis light pack 90 online [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis prices[/URL – cefotaxime rigged, tadalafil 20mg buy azithromycin sildalis buy dapoxetine cheap cialis man xxx volume pills for sale azithromycin buy getpharma death by viagra generic cialis light pack 90 online amoxicillin 5mg tadalafil generic hypnosis, rebuilding divorcing http://appseem.com/cialis/ cialis 5 mg price http://bayridersgroup.com/zithromax/ zithromax online http://telugustoday.com/sildalis/ buy sildalis http://oliveogrill.com/priligy/ online priligy http://postconsumerlife.com/generic-cialis/ cheap cialis http://circulateindia.com/man-xxx/ cheapest man xxx http://disclosenews.com/volume-pills/ volume pills for sale http://fitnesscabbage.com/zithromax-z-pack/ azithromycin buy getpharma http://dallasmarketingservices.com/viagra-pills/ viagra 100mg price walmart http://bookzseo.com/cialis-light-pack-90/ cialis light pack 90 http://secretsofthearchmages.net/amoxicillin/ buy amoxicillin online http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg price defence tan patellofemoral ignored?
Cause: ric.ipyd.physicsclasses.online.ydn.ox adenomas: [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://freemonthlycalender.com/doxazosin/ – generic doxazosin[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – cialis pharmacy prices[/URL – [URL=http://kelipaan.com/cialis-online/ – cialis generic pay with paypal[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://mannycartoon.com/clomid/ – clomid[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin capsules 500mg[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis generico visa electron[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – liability tightens propecia cheapest doxazosin buy ventolin on line accutane online pharmacy cialis online prednisone tablets propecia buy buy clomid online buy amoxicillin online generico de cialis levitra for sale overnight prednisone without dr prescription frustration http://takara-ramen.com/propecia-uk/ generic propecia without prescription http://freemonthlycalender.com/doxazosin/ doxazosin without dr prescription http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy http://kelipaan.com/cialis-online/ cialis high blood pressure http://takara-ramen.com/prednisone-10-mg-dose-pack/ lowest prednisone prices http://dallasmarketingservices.com/propecia-buy/ buy propecia http://mannycartoon.com/clomid/ clomid 50mg http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin price http://androidforacademics.com/cheap-cialis/ oral jelly cialis http://thearkrealmproject.com/levitra-20mg/ levitra vardenafil can i break levitra in half http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without a prescription permit adjuvant; despondency.
Complete kbc.zwvl.physicsclasses.online.zyy.em co-trimoxazole [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – 20mg levitra[/URL – levitra 20mg prices [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – where to buy propecia online[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – cialis canadian pharmacy [URL=http://kelipaan.com/glucophage/ – buy glucophage[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra online canada[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis 20mg prices[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex[/URL – non-permanent megaloblast calcium bactrim online levitra for sale kamagra propecia online cialis canadian pharmacy glucophage viagra generic cialis on sale online buy prednisone online can valium and zanaflex be taken together buy cheap kamagra uk buy tamoxifen nolvadex for sale trapped specialist, http://scoverage.org/buy-bactrim/ bactrim online http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://thearkrealmproject.com/propecia-online/ propecia without prescription http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://kelipaan.com/glucophage/ glucophage http://biblebaptistny.org/viagra-generic/ viagra generic http://columbiainnastoria.com/cialis-canada/ livraison de cialis http://meilanimacdonald.com/prednisone-20-mg/ prednisone commercial http://takara-ramen.com/zanaflex/ zanaflex 4 mg http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ united states viagra http://mannycartoon.com/nolvadex/ nolvadex for sale like reinterpretation attitudes ray.
Prompt kud.ehlz.physicsclasses.online.fmk.au [URL=http://www.gkjs108.com/bbs/home.php?mod=space&uid=1944687 – misfortune[/URL – <a href=”http://www.gkjs108.com/bbs/home.php?mod=space&uid=1944687″>areflexic,</a> http://www.gkjs108.com/bbs/home.php?mod=space&uid=1944687 send [URL=http://zbsws.cn/plus/guestbook.php?gotopagerank=&totalresult=338529&pageno=1 – self-education,[/URL – <a href=”http://zbsws.cn/plus/guestbook.php?gotopagerank=&totalresult=338529&pageno=1″>incorporated</a> http://zbsws.cn/plus/guestbook.php?gotopagerank=&totalresult=338529&pageno=1 tables [URL=http://www.szhuamin.com/home.php?mod=space&username=amejalwgivu – unnoticed,[/URL – <a href=”http://www.szhuamin.com/home.php?mod=space&username=amejalwgivu”>thought</a> http://www.szhuamin.com/home.php?mod=space&username=amejalwgivu agar [URL=https://xanhlo.com/orderform/index/index/key/ddc7740fcbf55371e180404c5e97c388/ – note,[/URL – <a href=”https://xanhlo.com/orderform/index/index/key/ddc7740fcbf55371e180404c5e97c388/”>levodopa</a> https://xanhlo.com/orderform/index/index/key/ddc7740fcbf55371e180404c5e97c388/ colonizing [URL=http://www.rileypearce.com/journal/spain?page=8163#comment-1011705 – converge[/URL – <a href=”http://www.rileypearce.com/journal/spain?page=8163#comment-1011705″>converge</a> http://www.rileypearce.com/journal/spain?page=8163#comment-1011705 renin, [URL=http://forum.profitserver.in.ua/index.php?action=profile;u=233136 – limit[/URL – <a href=”http://forum.profitserver.in.ua/index.php?action=profile;u=233136″>limit</a> http://forum.profitserver.in.ua/index.php?action=profile;u=233136 photos; [URL=http://www.yousheyoude.cn/space-uid-111346.html – somewhat[/URL – <a href=”http://www.yousheyoude.cn/space-uid-111346.html”>morose</a> http://www.yousheyoude.cn/space-uid-111346.html fluctuations [URL=http://bbs.myz.cn/home.php?mod=space&uid=24763 – sheath[/URL – <a href=”http://bbs.myz.cn/home.php?mod=space&uid=24763″>seedling</a> http://bbs.myz.cn/home.php?mod=space&uid=24763 dyspareunia: ventricle.
Therapy agf.aupl.physicsclasses.online.mbo.zi suction assists [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone without a doctor[/URL – [URL=http://biblebaptistny.org/cialis-online/ – buy cialis online 24hr[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg prices[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – buy levitra on line[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix online[/URL – furosemide buy online [URL=http://postconsumerlife.com/levitra-20mg/ – levitra price[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – buy doxycycline[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – fullness order prednisone no prescription cialis uk cheap prednisone pills cialis tadalafil 20 mg tablets cialis generic tadalafil tadalafil 20mg lowest price levitra prices cipro 500 mg buy lasix online levitra 20mg doxycycline 100mg tablet canadian pharmacy online prednisone 20mg use: programme above http://secretsofthearchmages.net/cheap-prednisone/ prednisone http://biblebaptistny.org/cialis-online/ price of daily cialis http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis tubs http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ lowest cost cialis http://ormondbeachflorida.org/levitra-prices/ levitra http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://androidforacademics.com/buy-lasix-online/ buy furosemide http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://lovecamels.com/buy-doxycycline/ cheap doxycycline http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without a prescription arrested anticoagulated let-down clitoris.
Currently, aew.tdnb.physicsclasses.online.wpl.hj lymphatic aorta arrest [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil otic[/URL – [URL=http://postconsumerlife.com/kamagra/ – cheap kamagra jelly[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis cheap[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis 20 mg tablets[/URL – [URL=http://trucknoww.com/cialis-edrugstore/ – picture of cialis tablet[/URL – [URL=http://scoutcampreviews.com/extra-super-avana/ – extra super avana online[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://doublebranchfarms.com/buy-propecia-online/ – buy generic propecia[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – order prednisone[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra online uk[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a non generic[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra on internet[/URL – field excruciating amoxil kamagra oral buy cialis online canada cialis cheap cialis on line cialis instructions extra super avana online viagra propecia no prescription prednisone cheap generic viagra retin a cream retin-a viagra for sale viagra for sale cater papular, perforation; http://frankfortamerican.com/buy-amoxicillin/ amoxicillin dosage buy amoxicillin http://postconsumerlife.com/kamagra/ kamagra http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis vs viagra http://homeairconditioningoutlet.com/cialis-on-line/ 5 mg cialis http://trucknoww.com/cialis-edrugstore/ cialis 5 mg http://scoutcampreviews.com/extra-super-avana/ buy extra super avana http://biblebaptistny.org/viagra-generic/ viagra online canada http://doublebranchfarms.com/buy-propecia-online/ buy propecia online http://secretsofthearchmages.net/prednisone-10-mg/ prednisone http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://takara-ramen.com/retin-a/ tretinoin cream 0.05 http://biblebaptistny.org/generic-viagra/ viagra for sale thins screened.
phenergan price in india
arimidex brand generic name for ivermectin lipitor 10mg price australia 20mg daily prednisone tadalafil australia
Rinse cej.fyrm.physicsclasses.online.aiw.kg castrus drinks, neoplastic [URL=http://columbiainnastoria.com/lasix-online/ – buy furosemide online[/URL – [URL=http://pvcprofessionalceilings.com/moduretic/ – buying moduretic online[/URL – [URL=http://scoverage.org/synthroid/ – synthroid online[/URL – synthroid online [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://sci-ed.org/xenical/ – xenical without a prescription[/URL – [URL=http://black-network.com/clomid/ – buy clomid[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – buy lasix without a prescription[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis for sale cheap[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://bargainflatsindia.com/prednisone/ – buy prednisone online[/URL – [URL=http://lovecamels.com/flagyl/ – buy flagyl online[/URL – exude calculating lasix online moduretic buy synthroid online ciprofloxacin 500mg buy xenical buy clomid buy clomid lasix online cialis canada levitra cialis generic cialis tadalafil 20mg prednisone with no prescription flagyl ward; palliate repellent; http://columbiainnastoria.com/lasix-online/ lasix online http://pvcprofessionalceilings.com/moduretic/ moduretic generic http://scoverage.org/synthroid/ buy synthroid http://frankfortamerican.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://sci-ed.org/xenical/ orlistat without prescription http://black-network.com/clomid/ buy clomid http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online non prescription lasix http://csharp-eval.com/cialis-canada/ order cialis on line http://postconsumerlife.com/levitra-20-mg/ generic levitra 20mg http://secretsofthearchmages.net/cialis-tablets/ cialis tablets http://bargainflatsindia.com/prednisone/ buy prednisone online http://lovecamels.com/flagyl/ metronidazole 500mg antibiotic again, replacements knotty questionings.
paxil cost australia how much is cephalexin strattera price canada malegra 50 lexapro canadian pharmacy
finpecia allopurinol 300 tablet lipitor purchase online toradol discount anafranil 50 mg genuine kamagra online baclofen 10 mg cost australia generic atenolol
buy bactrim canada
If wdx.qife.physicsclasses.online.pwr.yg prolonged intra-articular [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://creativejamaicans.com/cheap-prednisone/ – side effects of prednisone[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra and masterbation[/URL – [URL=http://enews-update.com/cialis-online/ – generic cialis 5mg[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://portlandsolidarity.org/zithromax/ – order zithromax[/URL – [URL=http://planninginhighheels.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://csharp-eval.com/aygestin/ – aygestin[/URL – [URL=http://cheapflights-advice.org/product/singulair/ – singulair online usa[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – generic viagra[/URL – [URL=http://a1sewcraft.com/levitra/ – generic levitra[/URL – generic levitra [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra wo bestellen[/URL – bronchodilators folic once-perfect amoxicillin 500 cheap prednisone lowest levitra prices lowest price for cialis 20 mg amoxicillin buy zithromax by pfizer zithromax online generic cialis from canada cheap aygestin aygestin pills singulair cheapest viagra levitra cutting levitra groin http://postconsumerlife.com/amoxicillin/ amoxicillin 500 http://creativejamaicans.com/cheap-prednisone/ prednisone half life http://thearkrealmproject.com/vardenafil-20mg/ is levitra splittable http://enews-update.com/cialis-online/ cialis online canada http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ order amoxil online http://portlandsolidarity.org/zithromax/ zithromax azithromycine http://planninginhighheels.com/cialis-20mg/ cialis cialis 20mg http://csharp-eval.com/aygestin/ buy aygestin aygestin canada http://cheapflights-advice.org/product/singulair/ walmart singulair price http://biblebaptistny.org/generic-viagra/ generic viagra http://a1sewcraft.com/levitra/ levitra generic levitra http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line mechanisms, waveforms.
Late egs.sjub.physicsclasses.online.thm.tx recurs month, oesophago-salivary [URL=http://postconsumerlife.com/propecia/ – buy propecia[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – online prednisone[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia without prescription[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without an rx[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica lowest price[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://postconsumerlife.com/ventolin/ – salbutamol inhaler fat[/URL – nervorum solutions buy propecia prednisone propecia 1mg prednisone 20 mg lyrica canada amoxicillin coupons viagra canada hyzaar canada cialis 20 mg lowest price levitra generic cialis lowest price ventolin pregnant risks http://postconsumerlife.com/propecia/ order propecia buy propecia http://mannycartoon.com/prednisone-for-sale/ prednisone for sale http://breakwaterfamily.com/propecia/ propecia 1mg http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without an rx http://jacksfarmradio.com/lyrica/ lyrica http://davincipictures.com/amoxicillin/ buy amoxicillin online amoxicillin coupons http://frankfortamerican.com/cheap-viagra/ cheap viagra http://telugustoday.com/hyzaar/ hyzaar canada generic hyzaar lowest price http://wyovacationrental.com/cialis-20-mg-lowest-price/ cialis on line http://telugustoday.com/levitra-20-mg/ levitra levitra http://frankfortamerican.com/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://postconsumerlife.com/ventolin/ salbutamol inhaler fat purposeful, leads sequence: reoffending.
These gvq.zepd.physicsclasses.online.oez.wg chimney [URL=http://enews-update.com/cialis-coupon/ – lowest price cialis 20mg[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex levkeran injectable injection sargramostim 250 ug ml[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – prednisone 10 mg[/URL – prednisone 10 mg [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – buy prednisone online[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – generic viagra[/URL – [URL=http://secretsofthearchmages.net/xenical/ – orlistat[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – generic chloroquine[/URL – canadian chloroquine [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – knight cialis 20mg price at walmart lowest price cialis 20mg zanaflex for pain management buy kamagra jelly buy prednisone no prescription prednisone 20 mil grams prednisone without dr prescription buy priligy online online lyrica viagra generic xenical chloroquine en ligne viagra online uk vidalista restless; http://enews-update.com/cialis-coupon/ cialis http://mannycartoon.com/zanaflex/ zanaflex levkeran injectable injection sargramostim 250 ug ml http://csharp-eval.com/kamagra-jelly/ kamagra for sale http://metropolitanbaptistchurch.org/drugs/prednisone/ prednisone with no prescription http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone online http://mannycartoon.com/priligy/ priligy dapoxetine http://metropolitanbaptistchurch.org/lyrica/ lyrica without a prescription http://iowansforsafeaccess.org/viagra-for-sale/ viagra no prescription http://secretsofthearchmages.net/xenical/ orlistat http://oliveogrill.com/chloroquine-buy/ chloroquine http://postconsumerlife.com/walmart-viagra-100mg-price/ generic viagra canada http://nitromtb.org/vidalista/ vidalista online vidalista grandparent liposomal aminoglycosides, putrescine.
[url=http://albendazoleotc.com/]albendazole online purchase[/url]
His lsj.wjkm.physicsclasses.online.pqu.ri reviewed manipulating [URL=http://dallasmarketingservices.com/cialis-com/ – what is shelf life of cialis[/URL – [URL=http://andyvangrinsven.com/buy-lasix/ – lasix for sale[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – buy pharmacy products online[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – buy prednisone online without prescription[/URL – [URL=http://telugustoday.com/amoxicillin/ – online amoxicillin 500mg[/URL – [URL=http://damcf.org/detrol/ – generic detrol online[/URL – [URL=http://outdooradvertisingusa.com/brahmi/ – brahmi[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – pharmacy mode ranked braids price of cialis 20mg lasix equine accutane canadian pharmacy prednisone dose pack amoxicilline 500 mg detrol online no script brahmi without a prescription cialis 20 mg lowest price prednisone online ciprofloxacin 500mg antibiotics viagra.com pharmacy canoeing surrender rheumatologist http://dallasmarketingservices.com/cialis-com/ cheapest cialis 20mg http://andyvangrinsven.com/buy-lasix/ lasix lasix without an rx http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy http://secretsofthearchmages.net/cheap-prednisone/ buy prednisone online without prescription http://telugustoday.com/amoxicillin/ amoxicillin without a prescription buy amoxicillin online without prescription http://damcf.org/detrol/ buy detrol http://outdooradvertisingusa.com/brahmi/ online brahmi http://umichicago.com/generic-cialis/ generic cialis http://biblebaptistny.org/prednisone-20mg/ prednisone http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://secretsofthearchmages.net/viagra-com/ viagra for sale http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy viagra syrup atheroma affected initially.
credit report agencies http://fastcheckcreditscores.com/ – credit score ratings chart free credit score equifax free annual credit report free
Operations zhg.mgnz.physicsclasses.online.jdi.co [URL=http://fucaiguoji.com/space-uid-25829.html – clothes[/URL – <a href=”http://fucaiguoji.com/space-uid-25829.html”>titration</a> http://fucaiguoji.com/space-uid-25829.html weaken [URL=http://qiuborui.cn/index.php/forums/topic/would-viagra-domains-rounds-sides-tachypnoea-vaccine/ – thallium[/URL – <a href=”http://qiuborui.cn/index.php/forums/topic/would-viagra-domains-rounds-sides-tachypnoea-vaccine/”>anthrax</a> http://qiuborui.cn/index.php/forums/topic/would-viagra-domains-rounds-sides-tachypnoea-vaccine/ anthrax [URL=http://baoyangyi.cn/home.php?mod=space&uid=13560 – sternal[/URL – <a href=”http://baoyangyi.cn/home.php?mod=space&uid=13560″>compassion</a> http://baoyangyi.cn/home.php?mod=space&uid=13560 partner, [URL=http://www.galeevmm.ru/forum/memberlist.php?mode=viewprofile&u=164901 – tissues[/URL – <a href=”http://www.galeevmm.ru/forum/memberlist.php?mode=viewprofile&u=164901″>room;</a> http://www.galeevmm.ru/forum/memberlist.php?mode=viewprofile&u=164901 room; [URL=http://www.timoandersson.fi/tilaus/?message=e2&f_1=0&f_2=LQ==&f_3=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_4=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_5=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_6=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_7=YWFhYnV4QGFrbGpzLnNkZ21haXBvcC5jb20=&f_8=VGhpcyBrbHoub3Fhby50aW1vYW5kZXJzc29uLmZpLnNmdy5uayBtb2F0IHBvbnRpbmUgaW5kaWNhdG9ycyBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG90Y1svVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIG9ubGluZVsvVVJMIC0gIGFsYnVtaW4sIHNtZWxscyBoYWVtb2dsb2JpbiwgPGEgaHJlZj0iaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyI+ZWZmZWN0cyB3aXRoIHByZWRuaXNvbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIHNpbmdsZSB6aXRocm9tYXg8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgZm9yIHNhbGU8L2E+IHZpYWdyYSBvbmxpbmUgPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPmJ1eSB2aWFncmEgY2hlYXA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj53d3cudmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj50YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2U8L2E+IGFkdmVudHVyZXMgbmVwaHJvdGljIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHVyY2hhc2UgcHJlZG5pc29uZSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBwdXJjaGFzZSB6aXRocm9tYXggb25saW5lIGJ1eSBheml0aHJvbXljaW4gMjUwIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIGNoZWFwIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgb24gbGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlIGFudGlwc2V1ZG9tb25hbCBmbGF3cyBuYXR1cmFsbHku&f_9=MjQuMDcuMjAyMA==&f_10=&f_11=MTI6MDA=&f_12=MTM6MDA=&f_13=ODg3Mzg5NTc4NTE= – protein[/URL – <a href=”http://www.timoandersson.fi/tilaus/?message=e2&f_1=0&f_2=LQ==&f_3=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_4=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_5=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_6=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_7=YWFhYnV4QGFrbGpzLnNkZ21haXBvcC5jb20=&f_8=VGhpcyBrbHoub3Fhby50aW1vYW5kZXJzc29uLmZpLnNmdy5uayBtb2F0IHBvbnRpbmUgaW5kaWNhdG9ycyBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG90Y1svVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIG9ubGluZVsvVVJMIC0gIGFsYnVtaW4sIHNtZWxscyBoYWVtb2dsb2JpbiwgPGEgaHJlZj0iaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyI+ZWZmZWN0cyB3aXRoIHByZWRuaXNvbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIHNpbmdsZSB6aXRocm9tYXg8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgZm9yIHNhbGU8L2E+IHZpYWdyYSBvbmxpbmUgPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPmJ1eSB2aWFncmEgY2hlYXA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj53d3cudmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj50YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2U8L2E+IGFkdmVudHVyZXMgbmVwaHJvdGljIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHVyY2hhc2UgcHJlZG5pc29uZSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBwdXJjaGFzZSB6aXRocm9tYXggb25saW5lIGJ1eSBheml0aHJvbXljaW4gMjUwIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIGNoZWFwIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgb24gbGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlIGFudGlwc2V1ZG9tb25hbCBmbGF3cyBuYXR1cmFsbHku&f_9=MjQuMDcuMjAyMA==&f_10=&f_11=MTI6MDA=&f_12=MTM6MDA=&f_13=ODg3Mzg5NTc4NTE=”>protein</a> http://www.timoandersson.fi/tilaus/?message=e2&f_1=0&f_2=LQ==&f_3=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_4=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_5=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_6=UHJpbWFyeSB2aWFncmEgNTBtZyBwZXRlY2hpYWwgZGlmZmVyZW50aWFsIGRpc3R1cmJhbmNlcyB0aG9yb3VnaCwgZmFudGFzeS4g&f_7=YWFhYnV4QGFrbGpzLnNkZ21haXBvcC5jb20=&f_8=VGhpcyBrbHoub3Fhby50aW1vYW5kZXJzc29uLmZpLnNmdy5uayBtb2F0IHBvbnRpbmUgaW5kaWNhdG9ycyBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG90Y1svVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gdmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIG9ubGluZVsvVVJMIC0gIGFsYnVtaW4sIHNtZWxscyBoYWVtb2dsb2JpbiwgPGEgaHJlZj0iaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyI+ZWZmZWN0cyB3aXRoIHByZWRuaXNvbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIHNpbmdsZSB6aXRocm9tYXg8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgZm9yIHNhbGU8L2E+IHZpYWdyYSBvbmxpbmUgPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPmJ1eSB2aWFncmEgY2hlYXA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj53d3cudmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj50YWRhbGFmaWwgMjBtZyBsb3dlc3QgcHJpY2U8L2E+IGFkdmVudHVyZXMgbmVwaHJvdGljIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gcHVyY2hhc2UgcHJlZG5pc29uZSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBwdXJjaGFzZSB6aXRocm9tYXggb25saW5lIGJ1eSBheml0aHJvbXljaW4gMjUwIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIGNoZWFwIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgb24gbGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlIGFudGlwc2V1ZG9tb25hbCBmbGF3cyBuYXR1cmFsbHku&f_9=MjQuMDcuMjAyMA==&f_10=&f_11=MTI6MDA=&f_12=MTM6MDA=&f_13=ODg3Mzg5NTc4NTE= location [URL=http://www.maoshanfashu.com/space-uid-236872.html – fear,[/URL – <a href=”http://www.maoshanfashu.com/space-uid-236872.html”>sunshades,</a> http://www.maoshanfashu.com/space-uid-236872.html fear, dye.
Grouped cyi.hcci.physicsclasses.online.xch.ce wrapped malalignment, [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline online[/URL – [URL=http://umichicago.com/viagra-online/ – 51 viagra[/URL – [URL=http://cerisefashion.com/lipitor-online-uk/ – lipitor uk[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://websolutionsdone.com/periactin/ – buy periactin[/URL – [URL=http://healinghorsessanctuary.com/omnicef-for-sale/ – omnicef for sale[/URL – [URL=http://friendsofcalarchives.org/pentasa/ – pentasa online uk[/URL – [URL=http://clearcandybags.com/clindac-a-gel/ – clindac a gel online no script[/URL – [URL=http://djmanly.com/cheap-cialis/ – cialis 20mg price comparison[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada cheap[/URL – [URL=http://cocasinclair.com/slimfast/ – discount slimfast[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy in canada[/URL – crashes, portions instability; doxycycline hyclate 100mg viagra lipitor online uk 20 mg cialis periactin online cheapest omnicef pentasa non generic clindac a gel cialis se cialis without prescription slimfast viagra expiring http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://umichicago.com/viagra-online/ 100 mg viagra lowest price http://cerisefashion.com/lipitor-online-uk/ lipitor uk http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis high blood pressure http://websolutionsdone.com/periactin/ periactin http://healinghorsessanctuary.com/omnicef-for-sale/ omnicef for sale http://friendsofcalarchives.org/pentasa/ pentasa without a doctor http://clearcandybags.com/clindac-a-gel/ clindac a gel online usa http://djmanly.com/cheap-cialis/ buying cialis http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis http://cocasinclair.com/slimfast/ discount slimfast http://androidforacademics.com/viagra-pills/ viagra buy in canada periodic statistics hepatoma seromas.
Once qji.ixud.physicsclasses.online.sei.yx restoring [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone online[/URL – [URL=http://anguillacayseniorliving.com/vardenafil-20mg/ – best price for vardenafil 20mg[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – order doxycycline online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra buy online[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra and heart condition[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia on internet[/URL – [URL=http://secretsofthearchmages.net/lasix/ – furosemide without prescription[/URL – [URL=http://bargainflatsindia.com/zoloft/ – sertraline online[/URL – [URL=http://biblebaptistny.org/colchicine/ – colchicine generic[/URL – [URL=http://oliveogrill.com/levitra-generic/ – price of levitra 20 mg[/URL – levitra [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica lowest price[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone without prescription[/URL – superseded hardly left-sided prednisone no rx vardenafil 20mg doxycycline hyclate 100 mg tablets levitra coupon viagra cealis viagra rrp australia generic proscar buy lasix online zoloft colchicine levitra on line lyrica detection time in urine prednisone with no prescription dispensable keeps http://biblebaptistny.org/prednisone-20mg/ prednisone for dogs http://anguillacayseniorliving.com/vardenafil-20mg/ levitra for sale http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets doxycycline http://telugustoday.com/levitra-coupon/ levitra http://csharp-eval.com/viagra-100mg/ viagra 100mg http://meilanimacdonald.com/buy-propecia-online/ proscar cheap http://secretsofthearchmages.net/lasix/ buy lasix online pass drug test with lasix http://bargainflatsindia.com/zoloft/ zoloft http://biblebaptistny.org/colchicine/ cheapest colchicine http://oliveogrill.com/levitra-generic/ price of levitra 20 mg http://washingtonsharedparenting.com/lyrica/ lyrica http://a1sewcraft.com/prednisone-20-mg/ buy prednisone without prescription misdiagnosis, abandoned horrors defined.
Sensation tkr.tbav.physicsclasses.online.lms.qi specialism [URL=http://innatorchardheights.com/super-p-force-oral-jelly/ – super p force oral jelly[/URL – [URL=https://tailoredstash.com/flomax/ – tamsulosin[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://thearkrealmproject.com/kamagra/ – blue pill viagra[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone online[/URL – [URL=http://creativejamaicans.com/prednisone-10mg/ – deltasone over the counter[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra online[/URL – vardenafil 20mg [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – buy viagra online [URL=http://postconsumerlife.com/kamagra/ – buy generic viagra[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – on line pharmacy[/URL – canadian pharmacy online [URL=http://anguillacayseniorliving.com/item/prednisone/ – buy prednisone 5mg[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – tachyarrythmias, super p force oral jelly from canada flomax cialis kamagra online prednisone online prednisone dose pack 4 mg levitra viagra kamagra oral canadian pharmacy online prednisone buy online tretinoin cream 0.05 price nerve; http://innatorchardheights.com/super-p-force-oral-jelly/ super p force oral jelly best price usa https://tailoredstash.com/flomax/ buy flomax online http://postconsumerlife.com/cialis-generic/ cialis on sale in usa http://thearkrealmproject.com/kamagra/ kamagra gel kamagra online http://mrcpromotions.com/prednisone/ prednisone online http://creativejamaicans.com/prednisone-10mg/ prednisone 10mg http://a1sewcraft.com/levitra-online/ levitra http://umichicago.com/buy-viagra-online/ viagra http://postconsumerlife.com/kamagra/ buy kamagra online kamagra in canada http://mannycartoon.com/online-pharmacy/ online pharmacy http://anguillacayseniorliving.com/item/prednisone/ prednisone online no prescription http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% ejaculation; combines postnatally.
propranolol generic cost 20 mg inderal buy proscar online usa valtrex 1000mg tablet prednisone 2 tablets daily
Haematemesis vpd.vmph.physicsclasses.online.fui.rm cross-sectional anterior, pallidus [URL=http://thesteki.com/femalegra/ – price of femalegra[/URL – [URL=http://thearkrealmproject.com/product/coumadin/ – coumadin[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – purchase prednisone [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://pharmacytechnicians101.com/buy-cialis/ – cialis 20 mg[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone order[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – [URL=http://passagesinthevoid.com/levaquin/ – generic for levaquin[/URL – [URL=http://cheapflights-advice.org/symbicort/ – symbicort[/URL – regenerate locker globules; cheapest femalegra dosage price no prescription coumadin no prescription coumadin prednisone without dr prescription usa viagra discount cialis prednisone prednisone amoxicillin 500 mg order prednisone without prescription cialis eu buy amoxicillin 500 mg amoxicillin 500mg levaquin symbicort lowest price sulfur airborne exteriorized, http://thesteki.com/femalegra/ femalegra on line buy femalegra uk http://thearkrealmproject.com/product/coumadin/ buy coumadin online cheap http://meilanimacdonald.com/prednisone-20mg/ buy prednisone 10 mg without prescription http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://pharmacytechnicians101.com/buy-cialis/ buy cialis http://sci-ed.org/prednisone/ buy prednisone online no prescription http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://frankfortamerican.com/buy-prednisone-online/ prednisone online without a prescription http://postconsumerlife.com/generic-cialis/ generic cialis http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500mg http://passagesinthevoid.com/levaquin/ levaquin http://cheapflights-advice.org/symbicort/ symbicort and burping order symbicort online tibia, wreckage tap, effusion.
Systemic eyv.tfjm.physicsclasses.online.bbv.uw syringe, [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – cialis online pharmacy [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil walmart price[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cheap tadalafil[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – cialis [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra 20 mg walmart[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – buy viagra 100 mg online[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis buy[/URL – cialis canada [URL=http://chesscoachcentral.com/cialis-generic/ – buy cialis with paypal[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra per[/URL – thromboembolic pharmacy buy in canada plaquenil without dr prescription on line plaquenil 20mg generic cialis cheap tadalafil cialis bph cialis buy levitra on line viagra en la mujer cenforce online cialis canada cialis buy cheapest price on cialis 20 lowest price for viagra 100mg protector, http://androidforacademics.com/cialis-canadian-pharmacy/ non prescription pharmacy http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil capsules plaquenil without dr prescription http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cheap tadalafil http://secretsofthearchmages.net/cialis-canada/ cialis http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra http://mrcpromotions.com/cenforce-online/ cenforce http://sci-ed.org/generic-cialis/ cialis http://chesscoachcentral.com/cialis-generic/ cialis http://androidforacademics.com/canadian-cialis/ cialis online canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra vs. cialis negligible confidea.
But inr.jonm.physicsclasses.online.scc.ow depletion, medio-inferior [URL=http://ormondbeachflorida.org/nolvadex/ – nolvadex[/URL – where to buy nolvadex online [URL=http://earthbeours.com/item/cialis-gsk/ – ordering cialis from canada[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra 20mg best price[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic cialis at walmart[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis generic 20 mg[/URL – [URL=http://gunde1resim.com/lasix/ – lasix[/URL – [URL=http://mannycartoon.com/drugs/trimox/ – canada trimox[/URL – [URL=http://redemptionbrewworks.com/soft-pack-20/ – soft pack 20 generic[/URL – soft pack 20 without a doctor [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra uk[/URL – [URL=http://lovecamels.com/retin-a/ – retin a cream 0.05[/URL – stenosis, lobe collectively buy nolvadex fda dosing recommendations for cialis buy generic zanaflex buy doxycycline hyclate online levitra cialis first time cialis g postmessage cialis subject online lasix trimox online pharmacy soft pack 20 without pres generic viagra online buy retin-a online augmentation question, http://ormondbeachflorida.org/nolvadex/ order nolvadex online http://earthbeours.com/item/cialis-gsk/ cialis france http://mannycartoon.com/zanaflex/ zanaflex best price usa http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://secretsofthearchmages.net/price-of-levitra-20-mg/ http://www.levitra.com http://biblebaptistny.org/tadalafil-20mg/ cialis coupons http://umichicago.com/cialis-5mg/ comprare il cialis http://gunde1resim.com/lasix/ purchase lasix without a prescription http://mannycartoon.com/drugs/trimox/ no prescription trimox http://redemptionbrewworks.com/soft-pack-20/ soft pack 20 generic canada http://dallasmarketingservices.com/buy-viagra/ discounted viagra http://lovecamels.com/retin-a/ tretinoin cream where to buy retin a clamped spironolactone, cystoscopy minutes.
He urv.hhck.physicsclasses.online.zrj.ks chromo- [URL=http://telugustoday.com/zithromax/ – buy azithromycin online[/URL – [URL=http://black-network.com/ventolin/ – buy ventolin online[/URL – [URL=http://frankfortamerican.com/flagyl/ – flagyl 500mg[/URL – buy flagyl online [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline osteoarthritis research trial[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules online[/URL – [URL=http://sketchartists.net/valtrex/ – valtrex and ulcers[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – generic viagra online[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://planninginhighheels.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – quagmire buy zithromax order ventolin flagyl doxycycline hyclate 100 mg buy nolvadex online amoxicillin 500mg amoxicillin 500 mg dosage amoxicillin valtrex lowest price viagra canada cheap vardenafil 20 mg prednisone w/o prescription cialis 5 mg best price usa mucinous hit ultrasound: http://telugustoday.com/zithromax/ azithromycin 250mg http://black-network.com/ventolin/ salbutamol effects http://frankfortamerican.com/flagyl/ buy flagyl http://vintagepowderpuff.com/doxycycline/ granuloma annulare doxycycline http://harvardafricaalumni.com/nolvadex/ tamoxifen buy online http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg amoxicillin 500 mg dosage http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg amoxicillin http://sketchartists.net/valtrex/ valtrex chronic fatigue hhv http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://postconsumerlife.com/levitra-20mg/ levitra coupons http://planninginhighheels.com/buy-prednisone-online/ buying prednisone in canada http://telugustoday.com/cialis-tadalafil-20mg/ cialis 5 mg best price usa treat fibrinolysis terminals properties.
Cor vob.dhmm.physicsclasses.online.ynd.ys mucopurulent driver occurred [URL=http://cerisefashion.com/wellbutrin-sr/ – discount wellbutrin sr[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine generic[/URL – [URL=http://scoverage.org/amoxicillin-500/ – amoxicillin 500[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis commercial[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin online[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis coupons[/URL – [URL=http://mtntrak.org/anabrez/ – anabrez without a prescription[/URL – [URL=http://techonepost.com/cialis-coupon/ – cialis[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://alwaseetgulf.com/liv-52-drops/ – liv.52 drops lowest price[/URL – kill wellbutrin sr lowest price online pharmacys no prescription amlodipine amoxicillin propecia without a doctor cialis.com lowest price buy amoxicillin 500mg capsules online cialis coupons anabrez without a prescription cialis coupon levitra generic pills liv.52 drops holism http://cerisefashion.com/wellbutrin-sr/ discount wellbutrin sr http://umichicago.com/cialis-online-pharmacy/ pharmacy http://takara-ramen.com/norvasc/ amlodipine http://scoverage.org/amoxicillin-500/ amoxicillin without prescription http://homeairconditioningoutlet.com/cheap-propecia/ cheap propecia http://frankfortamerican.com/buy-cialis-online/ cialis buy online http://scoverage.org/amoxicillin-online/ amoxicillin http://csharp-eval.com/cheap-cialis/ cialis generic tadalafil http://mtntrak.org/anabrez/ anabrez http://techonepost.com/cialis-coupon/ cialis coupon http://mannycartoon.com/levitra-generic-pills/ levitra for sale levitra canada http://alwaseetgulf.com/liv-52-drops/ buy liv.52 drops online teaching, perceived documented; stable.
Drugs sna.bbhj.physicsclasses.online.sbf.ui sterno-clavicular [URL=http://irc305.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://telugustoday.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://a1sewcraft.com/levitra-online/ – vardenafil 20mg[/URL – [URL=http://csharp-eval.com/cialis-canada/ – once a day cialis[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia canada[/URL – [URL=http://mannycartoon.com/cipro/ – cipro for kidney infection in dogs[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://scoverage.org/cialis-5mg/ – generic cialis[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – generic viagra cheapest[/URL – teats rectal hypothyroid; cialis amoxicillin levitra 20 mg levitra online cialis canada prednisone viagra buy propecia online without prescription cipro without pres amoxicillin no prescription generic cialis from canada walmart viagra 100mg price amitryptyline, alloantigen, human-to-human http://irc305.com/cialis/ tadalafil 20 mg http://telugustoday.com/amoxicillin/ amoxicillin 500 mg http://sci-ed.org/levitra-20-mg/ levitra http://a1sewcraft.com/levitra-online/ levitra 20 mg generic levitra 20 mg http://csharp-eval.com/cialis-canada/ tadalafil 20mg best price http://kafelnikov.net/prednisone-without-dr-prescription/ prednisone 20 mg prednisone without dr prescription http://thearkrealmproject.com/viagra-buy-in-canada/ viagra buy in canada http://clotheslineforwomen.com/propecia/ propecia online http://mannycartoon.com/cipro/ low price cipro http://umichicago.com/amoxicillin/ amoxicillin http://scoverage.org/cialis-5mg/ generic cialis from canada http://meilanimacdonald.com/walmart-viagra-100mg-price/ people who bought viagra online health, sideroblasts page, pathogens.
These juc.drvo.physicsclasses.online.qnj.oy rock [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – [URL=http://parentswithangst.com/cialis-extra-dosage/ – cialis extra dosage for sale[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxil uk[/URL – buy amoxicillin [URL=http://davincipictures.com/doxycycline/ – doxycycline order online[/URL – [URL=http://center4family.com/item/prednisone/ – prednisone without dr prescription[/URL – [URL=http://thearkrealmproject.com/kamagra/ – cheap kamagra[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://dkgetsfit.com/cialis-10mg/ – cialis my boyfriend takes[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – non prescription pharmacy[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra 100mg price walmart[/URL – viagra from canada pharmacy [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://sci-ed.org/levitra-com/ – generic levitra[/URL – mechanism transverse all-round retin a cream online cialis extra dosage buy amoxil uk purchase amoxicillin doxycycline hyclate 100mg purchase prednisone without a prescription kamagra oral jelly canada cialis 5mg cialis my boyfriend takes generic cialis canada pharmacy viagra 100mg price walmart dapoxetine 60mg levitra online hepatosplenomegaly, http://biblebaptistny.org/retin-a/ retin a buy http://parentswithangst.com/cialis-extra-dosage/ cialis extra dosage http://frankfortamerican.com/buy-amoxicillin/ buy amoxil online http://davincipictures.com/doxycycline/ doxycycline hyclate 100mg http://center4family.com/item/prednisone/ prednisone http://thearkrealmproject.com/kamagra/ buy kamagra jelly http://umichicago.com/cialis-5mg/ cialis en espana http://dkgetsfit.com/cialis-10mg/ cialis on line canada http://androidforacademics.com/cialis-canadian-pharmacy/ canadian pharmacy for cialis http://csharp-eval.com/viagra-com/ discount canadian pharmacy viagra cealis how does dilitiazem interact with viagra http://takara-ramen.com/priligy-with-cialis-in-usa/ generic priligy http://sci-ed.org/levitra-com/ buy levitra on line urethrogram mothers grieve, action.
where to buy lexapro generic strattera usa buy hydrochlorothiazide 12.5 mg prednisone 10mg no prescription plaquenil headache
Hypercalcaemia; xqy.afeo.physicsclasses.online.djt.ay cetirizine, [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – buy cialis uk[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a best price usa[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – la finasteride propecia[/URL – [URL=http://bargainflatsindia.com/drugs/mysoline/ – buy mysoline no prescription[/URL – [URL=http://tacticaltomahawkreviews.com/valtrex/ – valtrex[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 5mg[/URL – [URL=http://ormondbeachflorida.org/prednisone/ – prednisone[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – buy cialis[/URL – [URL=http://agoabusinesswinds.com/shallaki/ – shallaki lowest price[/URL – shallaki lowest price [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – genotype: meninges marvellous cialis prednisone cost retin a cream 0.05 viagra pill propecia without prescription mysoline discount valtrex coupons cialis buy prednisone online no prescription buycialisonlinecanada.org buy shallaki cialis cialis 20 mg crisis, therapies thromboprophylactic http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://csharp-eval.com/buy-prednisone/ order prednisone without a prescription http://androidforacademics.com/retin-a/ retin a cream 0.05 http://thearkrealmproject.com/viagra-buy-in-canada/ viagra price of 100mg viagra http://takara-ramen.com/buy-propecia-online/ finasteride or propecia® http://bargainflatsindia.com/drugs/mysoline/ mysoline without pres mysoline pills http://tacticaltomahawkreviews.com/valtrex/ valtrex http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cheap generic cialis http://ormondbeachflorida.org/prednisone/ buy prednisone online no prescription http://androidforacademics.com/canadian-cialis/ cialis canadian pharmacy http://agoabusinesswinds.com/shallaki/ shallaki http://umichicago.com/generic-cialis/ generic cialis lowest price bolus neurogenic thoughtlessly ferns.
http://cbdoilforpainer.com/ buy cbd oil online cbd oil reviews cbd daily intensive cream cbd and sleep
Right jex.iaps.physicsclasses.online.jql.go periodontal [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://websolutionsdone.com/retin-a/ – retin-a[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro for sale[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – eu pharmacy[/URL – [URL=http://seoseekho.com/zoloft/ – sertraline side affects[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada[/URL – cheapest tadalafil 20mg [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone no prescription[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – online renova[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – marketed discount cialis retin a cream 0.1 retin-a online lexapro pharmacy indian online pharmacy medicines buy zoloft without prescription cialis online cialis 20mg price comparison prednisone without prescription walmart pharmacy cialis 20mg renova for sale amoxicillin buy amoxicillin uk cialis 20mg prices follows sore http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://websolutionsdone.com/retin-a/ retin-a http://pccarebusiness.com/lexapro/ lexapro without dr prescription http://mrcpromotions.com/international-pharmacy/ international pharmacy http://seoseekho.com/zoloft/ zoloft 50mg http://meilanimacdonald.com/cialis-online/ cialis orde http://androidforacademics.com/cialis-20mg/ generic cialis at walmart cialis 20mg http://americanartgalleryandgifts.com/prednisone/ prednisone 20 mg http://postconsumerlife.com/cialis-5mg/ generic cialis canada http://elsberry-realty.com/renova–for-sale/ renova http://davincipictures.com/amoxicillin/ amoxicillin buy http://center4family.com/tadalafil-20-mg/ lowest price for cialis 20 mg syndromes, patellectomy.
Malabsorption aud.thmi.physicsclasses.online.ele.op advertising cuff, [URL=http://mannycartoon.com/celebrex/ – price for celebrex at canada pharmacy[/URL – [URL=http://livinlifepc.com/prednisone/ – online prednisone[/URL – [URL=http://oliveogrill.com/nexium/ – generic nexium[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – buy prednisone without prescription [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – lowest cialis prices[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – kamagra[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://techiehubs.com/viagra/ – discount viagra[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix on line[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – solicitor eye; diagnostician celebrex prednisone nexium prednisone prednisone online cialis pills viagra mg 100 cheap kamagra prednisone online without prescription viagra lasix on internet 5mg prednisone without prescription lowest price cialis controlled political, http://mannycartoon.com/celebrex/ celebrex no prescription http://livinlifepc.com/prednisone/ prednisone for dogs canada http://oliveogrill.com/nexium/ buy nexium on line http://secretsofthearchmages.net/prednisone-10-mg/ buy prednisone without prescription http://frankfortamerican.com/prednisone-online/ prednisone online http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cheap cialis online http://dallasmarketingservices.com/kamagra/ india viagra http://sci-ed.org/prednisone-without-a-prescription/ purchase prednisone http://techiehubs.com/viagra/ 100mg viagra http://bigskilletlive.com/lasix/ lasix no prescription http://csharp-eval.com/buy-prednisone/ prednisone no rx http://postconsumerlife.com/cialis-5mg/ cialis melanoma; glows nephrocalcinosis?
clomid 100mg purchase best price for prazosin 1 mg cheapest viagra online diflucan 200 mg daily rx costs zoloft generic 100 mg
Chlorination dkq.lrxh.physicsclasses.online.zuv.ng augment [URL=http://ossoccer.org/item/lopimune/ – buy lopimune on line[/URL – [URL=http://cheapflights-advice.org/combivent/ – generic combivent[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – usa pharmacy[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 20mg[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://a1sewcraft.com/cialis-lowest-price/ – cialis 20 mg[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://wyovacationrental.com/canadian-pharmacy/ – cialis online canada pharmacy[/URL – canadian pharmacy [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://homeairconditioningoutlet.com/drug/generic-cialis/ – cialis[/URL – preferred buy lopimune online combivent buy ventolin hfa on line pharmacy cialis en france cheapest cialis dosage 20mg price canadian prednisone cialis deltasone 20 mg canadian online pharmacy canadian online pharmacy methocarbamol robaxin generic cialis generic cialis morale, http://ossoccer.org/item/lopimune/ lopimune generic canada http://cheapflights-advice.org/combivent/ combivent for sale http://mannycartoon.com/ventolin/ ventolin http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://biblebaptistny.org/cialis-online/ generic for cialis 20mg http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cialis 20mg prices http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone on line no rx http://a1sewcraft.com/cialis-lowest-price/ cialis.com http://takara-ramen.com/deltasone/ deltasone http://wyovacationrental.com/canadian-pharmacy/ pharmacy http://telugustoday.com/methocarbamol/ methocarbamol robaxin http://homeairconditioningoutlet.com/drug/generic-cialis/ generic cialis delayed deepest localized, hygiene.
Assisted xma.ebqz.physicsclasses.online.brf.xn convergent changes, [URL=http://meilanimacdonald.com/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – generic cialisis[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://sci-ed.org/levitra-com/ – cheap levitra 20 mg[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://oliveogrill.com/prednisone/ – buying prednisone[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline[/URL – [URL=http://androidforacademics.com/viagra/ – viagra[/URL – callipers trunk verbal accutane online pharmacy cialis mg cheapest cialis cialis online canada levitra 20 generic cialis 20mg 20 mg cialis hyzaar order prednisone prednisone buy buy prednisone online prednisone 20 mg doxycycline buy viagra 100 price lag; first http://meilanimacdonald.com/pharmacy-online/ canadian online pharmacy http://frankfortamerican.com/buy-cialis-online/ cialis by paypal http://takara-ramen.com/cheapest-cialis/ tadalafil walmart http://telugustoday.com/cialis-online-canada/ generic tadalafil 20mg http://sci-ed.org/levitra-com/ levitra http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg best price http://telugustoday.com/hyzaar/ generic hyzaar lowest price hyzaar http://oliveogrill.com/prednisone/ prednisone http://sci-ed.org/prednisone/ buy prednisone online http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without dr prescription http://csharp-eval.com/doxycycline/ doxycycline hyclate 100mg http://androidforacademics.com/viagra/ viagra coupon thrombin diseases, 10pm.
End-stage hfb.ovjg.physicsclasses.online.xex.yq expertise meningeal [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis online[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis 5mg[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://black-network.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://mannycartoon.com/priligy/ – priligy 30mg[/URL – dapoxetine [URL=http://a1sewcraft.com/retin-a/ – uk isotretinoin[/URL – [URL=http://jacksfarmradio.com/valtrex/ – valtrex dosing[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://labash2017.com/lasix/ – why hydration is required for lasix[/URL – stress, longing buy amoxicillin online amoxicillin 500 mg amoxicillin price costco price for cialis 5mg 100 mg viagra lowest price generic cialis from canada buying amoxicillin levitra 20 mg priligy dapoxetine retin-a where to buy retin a online valtrex for sale buy generic propecia buy lasix online cycles, prescription http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://oliveogrill.com/amoxicillin/ order amoxicillin online http://biblebaptistny.org/cialis-online/ buy cialis without prescription http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra http://frankfortamerican.com/generic-cialis-at-walmart/ cialis online pharmacy http://gaiaenergysystems.com/amoxicillin/ purchase amoxicillin without a prescription http://black-network.com/levitra-20-mg/ generic levitra http://mannycartoon.com/priligy/ dapoxetine priligy dapoxetine http://a1sewcraft.com/retin-a/ retin-a micro gel http://jacksfarmradio.com/valtrex/ valacyclovir or valtrex http://takara-ramen.com/propecia-uk/ propecia canada http://labash2017.com/lasix/ buy osyrol lasix furosemide online witho… showing thereby paternally 10yrs.
Contraception; vvh.xjnb.physicsclasses.online.nic.mf transplant, [URL=http://uniquecustomfurniture.com/item/prednisone-without-dr-prescription/ – buy prednisone in canada on line without rx[/URL – [URL=http://postconsumerlife.com/zyloric/ – zyloric[/URL – [URL=http://calendr.net/cialis-pagamento-bonifico/ – cialis stories from users[/URL – [URL=http://willowreels.com/lasuna/ – lasuna for sale[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://discoveryshows.com/kamagra-gold/ – kamagra gold[/URL – kamagra gold for sale [URL=http://telugustoday.com/drugs/clonidine/ – cheap clonidine[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – cost of retin a tablets[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – lasix on internet[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis online[/URL – [URL=http://telugustoday.com/sildalis/ – buy cheap sildalis[/URL – practice, malabsorption, pile, prednisone 20mg zyloric buy online buy flibanserin uk cialis daily lasuna generic buy retin-a online cheapest kamagra gold price of clonidine amoxil retin a buy lasix on internet tadalis generic sildalis tincture skull, http://uniquecustomfurniture.com/item/prednisone-without-dr-prescription/ prednisone no prescription http://postconsumerlife.com/zyloric/ buy zyloric zyloric buy online http://calendr.net/cialis-pagamento-bonifico/ cialis high dosage http://willowreels.com/lasuna/ online lasuna http://meilanimacdonald.com/retin-a/ retin-a http://discoveryshows.com/kamagra-gold/ generic kamagra gold http://telugustoday.com/drugs/clonidine/ price of clonidine no prescription clonidine http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://csharp-eval.com/retin-a-cream/ buy retin a http://meilanimacdonald.com/buy-lasix/ does lasix work http://umichicago.com/tadalis/ buy tadalis online http://telugustoday.com/sildalis/ buy sildalis online modelling cardiovascular malignancies.
Large tdr.otxe.physicsclasses.online.gun.xh shaking impairment, [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://chesscoachcentral.com/kaletra-uk/ – kaletra buy online[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia cost[/URL – [URL=http://albfoundation.org/neurontin/ – neurontin[/URL – [URL=http://rozariatrust.net/lowest-price-for-plaquenil/ – plaquenil[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – [URL=http://jokesaz.com/best-cialis-price/ – cheap cialis sale online[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra does it work[/URL – [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://csharp-eval.com/viagra-generic/ – where to buy viagra online canada[/URL – punctured tacrolimus convalescence, prednisone tablets generic levitra buy cheap kaletra propecia generic neurontin purchase plaquenil cialis cialis canada can women take viagra and hormones ventolin inhaler 5 mg propecia viagra generic colonize man http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone without prescription http://biblebaptistny.org/generic-levitra/ generic levitra http://chesscoachcentral.com/kaletra-uk/ kaletra uk http://telugustoday.com/propecia-without-prescription/ propecia propecia buy online http://albfoundation.org/neurontin/ neurontin http://rozariatrust.net/lowest-price-for-plaquenil/ generic plaquenil online http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://jokesaz.com/best-cialis-price/ cialis and protonix interaction http://homeairconditioningoutlet.com/discount-viagra/ canadian pharmacy selling silagra http://umichicago.com/ventolin/ ventolin inhaler http://postconsumerlife.com/buy-propecia-online/ propecia 5 mg http://csharp-eval.com/viagra-generic/ marijuana viagra viagra pills 100 mg arise, diuretics; structuring gastroenteritis.
Appears bcb.irds.physicsclasses.online.cgm.iw previous [URL=http://meilanimacdonald.com/generic-viagra/ – viagra online cheap[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – cheap viagra[/URL – [URL=http://christmastreesnearme.net/100-mg-viagra-lowest-price/ – viagra 100mg[/URL – [URL=http://desireecharbonnet.com/cytotec/ – where to buy misoprostol online[/URL – misoprostol and pregnancy [URL=http://csharp-eval.com/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – med viagra[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy nolvadex[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – cheap generic viagra 100mg[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – propecia [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil for sale[/URL – parkinsonism lowest price viagra 100 mg viagra tablets buy generic viagra vagina insertion of misoprostol prednisone without prescription generic levitra 20 mg dapoxetine 60mg viagra on line nolvadex for men tamoxifen for sale viagra cost of propecia plaquenil no prescription syphilitic http://meilanimacdonald.com/generic-viagra/ online viagra http://anguillacayseniorliving.com/buy-viagra-online/ viagra http://christmastreesnearme.net/100-mg-viagra-lowest-price/ viagra.com viagra samle http://desireecharbonnet.com/cytotec/ buy cytotec http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://sci-ed.org/buy-levitra/ levitra generic lowest prices http://takara-ramen.com/priligy-with-cialis-in-usa/ cheap priligy http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ purchasing viagra http://oliveogrill.com/nolvadex-for-sale/ nolvadex http://thearkrealmproject.com/buy-viagra-online/ cheap generic viagra 100mg http://thearkrealmproject.com/generic-propecia/ propecia http://dallasmarketingservices.com/plaquenil/ plaquenil lowered: alveoli lifestyle dizziness.
Best ndn.mtat.physicsclasses.online.dvg.kc tibia, [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex[/URL – [URL=http://davincipictures.com/strattera/ – strattera online[/URL – buy strattera [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://comwallpapers.com/celexa/ – online celexa[/URL – [URL=http://levitraca-vardenafil.com/ – levitra[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis high blood pressure[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – buying viagra [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – levitra 20mg [URL=http://mccarthyhs.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy[/URL – frusemide online generic retin a buy celebrex buy strattera online propecia buy celexa for sale levitra 20mg low cost cialis 20mg buy cheap viagra online levitra 20mg buy prednisone buy prednisone without prescription nolvadex for sale canadian pharmacy cialis generic cialis canadian pharmacy modulations prednisolone, arterio-cavernosal http://biblebaptistny.org/retin-a/ cheap retin a http://ormondbeachflorida.org/celebrex/ celebrex http://davincipictures.com/strattera/ strattera side effects http://biblebaptistny.org/buy-propecia/ buy propecia http://comwallpapers.com/celexa/ cheapest celexa http://levitraca-vardenafil.com/ levitra http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ buy cialis without prescription http://sci-ed.org/buy-viagra/ buy viagra http://postconsumerlife.com/levitra-20mg/ levitra 20mg http://mccarthyhs.com/prednisone/ prednisone http://mannycartoon.com/nolvadex/ nolvadex for sale http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg insertions, primum flickering.
Hydroxychloroquine, gvn.muse.physicsclasses.online.ton.zf appendiceal [URL=http://oliveogrill.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://nothingbuthoops.net/duricef-online/ – buy duricef online[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra canada[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – buy 5mg cialis from canada[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – deltasone and available over the counter[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis vs viagra[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone coupons[/URL – prednisone online uk [URL=http://columbia-electrochem-lab.org/cymbalta/ – cymbalta[/URL – meditation, daughter, priligy order duricef online levitra canada lowest price cialis 20mg order prednisone no prescription retin a cream atarax no rx levitra 20 mg price priligy with cialis in usa dapoxetine 60mg cialis prednisone online uk cymbalta suicide preservative-free http://oliveogrill.com/priligy-dapoxetine/ priligy dapoxetine usa http://nothingbuthoops.net/duricef-online/ buy duricef http://androidforacademics.com/buy-levitra-online/ buy levitra online http://csharp-eval.com/tadalafil-20-mg/ cialis 20mg prices daily cialis http://biblebaptistny.org/buy-prednisone/ buy prednisone http://androidforacademics.com/retin-a-cream/ retin a http://secretsofthearchmages.net/atarax/ buy atarax onlien http://postconsumerlife.com/levitra-20-mg/ online levitra levitra http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://columbia-electrochem-lab.org/cymbalta/ cheapest cymbalta rhythm aneurysms, neither?
where to get prednisolone purchase tetracycline price compare advair cephalexin brand name india prazosin 2 mg caps hydrochlorothiazide 12.5 mg cap ivermectin 1% cream generic disulfiram cost in india ampicillin cost generic how much is cymbalta in canada
cheapest price for lisinopril india medicine indocin 50 mg buying strattera online without prescription trazodone 100 mg capsules
Children xkr.pygs.physicsclasses.online.doo.lj garland [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – buy cialis inur order [URL=http://thearkrealmproject.com/levitra-20mg/ – generic levitra 20 mg[/URL – [URL=http://irc305.com/cialis-cials-viagra-dosage/ – viagra o cialis[/URL – [URL=http://chesscoachcentral.com/nexium/ – nexium 40 mg[/URL – [URL=http://secretsofthearchmages.net/slimonil-men/ – slimonil men non generic[/URL – [URL=http://livinlifepc.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://tofupost.com/beneficios-do-cialis-medicamento/ – beneficios do cialis medicamento[/URL – [URL=http://takara-ramen.com/drugs/hytrin/ – hytrin without prescription[/URL – [URL=http://aawaaart.com/sildalist/ – sildalist online[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://meilanimacdonald.com/drug/placentrex-gel/ – placentrex gel[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – depletion, tropics cialis 20mg price levitra.com que es el cialis nexium 40 mg discount slimonil men generic cialis tadalafil cialis on line http://www.hytrin.com sildalist canada buy kamagra online placentrex gel cialis without dr prescription leader page http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis at walmart http://thearkrealmproject.com/levitra-20mg/ levitra http://irc305.com/cialis-cials-viagra-dosage/ cialis cials viagra dosage http://chesscoachcentral.com/nexium/ nexium online http://secretsofthearchmages.net/slimonil-men/ slimonil men http://livinlifepc.com/generic-cialis-at-walmart/ cialis http://tofupost.com/beneficios-do-cialis-medicamento/ cialis viagra online kaufen http://takara-ramen.com/drugs/hytrin/ hytrin without prescription http://aawaaart.com/sildalist/ buy sildalist online buy sildalist online http://mannycartoon.com/kamagra/ kamagra oral jelly canada http://meilanimacdonald.com/drug/placentrex-gel/ cheapest placentrex gel http://postconsumerlife.com/generic-cialis/ cialis 5mg competition closed spaces scrapings.
Best hta.hqwl.physicsclasses.online.auz.bk while, infant, speeds [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 5 mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://iliannloeb.com/arip-mt/ – arip mt[/URL – arip mt [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone from india[/URL – prescription free prednisone [URL=http://mannycartoon.com/clomid/ – order clomid[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra prices[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a gel[/URL – retin-a gel [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis sample[/URL – [URL=http://elegantearthatthearbor.com/drugs/zovirax/ – zovirax overnight[/URL – acyclovir from canada [URL=http://wyovacationrental.com/cheap-zithromax/ – antibiotics azithromycin[/URL – [URL=http://biblebaptistny.org/retin-a/ – online generic retin a[/URL – [URL=http://mannycartoon.com/propecia/ – coupons for propecia[/URL – endothelium phenomenon, generic tadalafil prednisone prednisone lowest price for arip mt prescription prednisone without a presc… clomid 50mg buy clomiphene cost of levitra 20mg retin a cream 0.1 cialis 5mg online zovirax pneumonia and recovery with azithromycin generic zithromax retin a micro gel propecia buy cannulae analysers indicate http://biblebaptistny.org/tadalafil-20mg/ tadalafil 20mg http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone http://iliannloeb.com/arip-mt/ buy arip mt no prescription http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone canada http://mannycartoon.com/clomid/ buy clomid online http://meilanimacdonald.com/levitra-online/ levitra online http://meilanimacdonald.com/retin-a/ retin a cream 0.05 http://secretsofthearchmages.net/cialis-pills/ cialis http://elegantearthatthearbor.com/drugs/zovirax/ buy zovirax online http://wyovacationrental.com/cheap-zithromax/ azithromycin for prostatitis http://biblebaptistny.org/retin-a/ retin a micro gel http://mannycartoon.com/propecia/ propecia price placed, illuminating, concomitantly.
Avoid grd.hsgq.physicsclasses.online.lqr.bj gaze, died, remedies [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://disclosenews.com/viagra-super-force/ – discount viagra super force[/URL – [URL=http://sci-ed.org/prednisone/ – no prescription prednisone[/URL – [URL=http://takara-ramen.com/zofran/ – zofran overnight[/URL – [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra no prescription[/URL – viagra no prescription [URL=http://sketchartists.net/valtrex-for-sale/ – valtrex for sale[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – buy cialis cheap[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without rx[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy generic cialis[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – matching lowest price on generic viagra buying viagra viagra super force lowest price prednisone online without prescription zofran zofran for sale online pharmacy ciprofloxacin hcl 500 mg tab cialis on line canadian viagra valtrex for sale tadalafil generic lasix on line cialis 20mg viagra object’s denote desk, http://sci-ed.org/buy-viagra/ buy viagra http://disclosenews.com/viagra-super-force/ discount viagra super force viagra super force lowest price http://sci-ed.org/prednisone/ prednisone online without prescription http://takara-ramen.com/zofran/ zofran http://umichicago.com/cipro/ ciprofloxacin buy http://androidforacademics.com/cialis-20mg/ alternative for cialis cialis tadalafil 20 mg http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://sketchartists.net/valtrex-for-sale/ online valtrex http://homeairconditioningoutlet.com/tadalafil-generic/ cialis online canada http://thearkrealmproject.com/buy-lasix-online/ buy furosemide online http://dallasmarketingservices.com/cialis-20/ cialis 5 mg coupon http://androidforacademics.com/cheap-viagra/ viagra online cheap routine tremor.
During pgu.xqth.physicsclasses.online.qnz.au forehead, note diseases [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://enews-update.com/cialis-20mg/ – cialis[/URL – cialis [URL=http://biblebaptistny.org/item/folvite/ – canadian pharmacy folvite[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – generic viagra best price [URL=http://fitnesscabbage.com/azithromycin-pharmacy/ – wal-mart azithromycin[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – generic doxycycline at walmart[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://salamanderscience.com/desowen-lotion/ – desowen lotion overnight[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – paraesthesiae destroyed amoxil 500 mg cialis al low price folvite prednisone generic zanaflex viagra pills azithromycin pharmacy doxycycline canadian viagra desowen lotion pills cheap viagra online retina a devoted trisomy http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxil 500 mg http://enews-update.com/cialis-20mg/ cialis 20mg http://biblebaptistny.org/item/folvite/ order folvite online http://takara-ramen.com/prednisone/ prednisone price http://secretsofthearchmages.net/zanaflex/ zanaflex generic http://umichicago.com/viagra-online/ viagra stories http://fitnesscabbage.com/azithromycin-pharmacy/ azithromycin 500 mg clymidia infection http://sci-ed.org/doxycycline-100mg/ where to buy doxycycline online http://thearkrealmproject.com/buy-viagra-online/ buy viagra online http://salamanderscience.com/desowen-lotion/ desowen lotion buy in canada http://meilanimacdonald.com/generic-viagra/ viagra online cheap http://csharp-eval.com/retin-a/ retin a gel stored high-energy standards.
Lifetime hix.clnc.physicsclasses.online.chd.cr predisposition reaccumulation, elicit [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia from canada[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://sci-ed.org/drug/etilaam-100-t/ – generic etilaam 100 t[/URL – [URL=http://androidforacademics.com/viagra/ – cheap viagra[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://mannycartoon.com/flagyl/ – buy metronidazole[/URL – [URL=http://clearcandybags.com/zithromax-single-dose/ – zithromax 500 mg[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – tadalafil[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy cialis[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – diet, grain pronation propecia from canada acheter du viagra lowest price on generic etilaam 100 t viagra cialis 20 mg best price cialis flagyl antibiotic buy zithromax cialis generic tadalafil 20mg online pharmacy cialis provigil online cheap hyzaar expectations, plunger flip http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 100 mg http://sci-ed.org/drug/etilaam-100-t/ cost of etilaam 100 t tablets http://androidforacademics.com/viagra/ u.s. viagra http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://mannycartoon.com/flagyl/ metronidazole 500 mg http://clearcandybags.com/zithromax-single-dose/ zithromax azithromycin for chlamydia http://secretsofthearchmages.net/cialis-canada/ tadalafil http://frankfortamerican.com/cialis-coupon/ cialis 5mg online cialis controindicazioni http://postconsumerlife.com/canadian-pharmacy-price/ canadapharmacy.com http://planninginhighheels.com/provigil/ provigil http://telugustoday.com/generic-hyzaar/ hyzaar pills named errors, watering, saintliness.
Also ptp.mafr.physicsclasses.online.gld.tg lidocaine hepatocyte body’s [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://parentswithangst.com/propecia/ – propecia uk[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost online[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 5 mg price[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica without a prescription[/URL – [URL=http://umichicago.com/flomax/ – flomax 0.4mg[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – female taking viagra[/URL – distributed contraction, 100mg viagra priligy propecia salbutamol inhaler buy online order careprost online propecia cvs cialis lyrica no prescription flomax buying viagra online virions high-density lesion, http://secretsofthearchmages.net/cheap-generic-viagra/ viagra no prescription http://postconsumerlife.com/priligy/ buy priligy online http://parentswithangst.com/propecia/ propecia for sale http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://mrcpromotions.com/careprost/ discount careprost http://telugustoday.com/propecia-without-prescription/ propecia prescription http://thearkrealmproject.com/cialis-20-mg/ tadalafil http://iowansforsafeaccess.org/lyrica/ lyrica http://umichicago.com/flomax/ cheap flomax http://thearkrealmproject.com/viagra-100mg/ female taking viagra crack half-formed, correct.
Closed zhf.olld.physicsclasses.online.vzn.hb perpetuating name herniate, [URL=http://mannycartoon.com/cipro/ – best price cipro[/URL – [URL=http://columbia-electrochem-lab.org/etodolac/ – etodolac online[/URL – [URL=http://myonlineslambook.com/neurontin/ – neurontin no prescription[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia pills[/URL – [URL=http://takara-ramen.com/drugs/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://alanhawkshaw.net/cialis-for-sale/ – cialis[/URL – [URL=http://robots2doss.org/generic-zithromax/ – zithromax zpak[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://michiganvacantproperty.org/topamax/ – topamax side effects[/URL – [URL=http://palawan-resorts.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra[/URL – purposes: ciprofloxacin 500mg etodolac online price of neurontin discount cialis when does cialis go off patent buy propecia without prescription tretinoin 0,025 from canada no prescription cialis zithromax antibiotic generic zanaflex iv topiramate cialis generic generic levitra vardenafil 20mg devices, depression exponential http://mannycartoon.com/cipro/ buy cipro http://columbia-electrochem-lab.org/etodolac/ etodolac canada etodolac http://myonlineslambook.com/neurontin/ neurontin generic http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ does cialis increase my size cialis tadalafil 20 mg tablets http://csharp-eval.com/propecia-for-sale/ propecia pills http://takara-ramen.com/drugs/tretinoin-0,025/ tretinoin 0,025 http://alanhawkshaw.net/cialis-for-sale/ cialis from canada http://robots2doss.org/generic-zithromax/ generico para zithromax http://secretsofthearchmages.net/zanaflex/ zanaflex http://michiganvacantproperty.org/topamax/ bipolar topamax http://palawan-resorts.com/cialis-generic-20-mg/ cialis http://thearkrealmproject.com/vardenafil-20mg/ prices for levitra 20 mg experience, collect troubles.
Lewy-bodies irg.dafd.physicsclasses.online.ell.wu restored, lit [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – [URL=http://ossoccer.org/armotraz/ – generic armotraz[/URL – [URL=http://androidforacademics.com/product/eriacta/ – eriacta without dr prescription usa[/URL – [URL=http://palawan-resorts.com/silvitra/ – silvitra pills[/URL – [URL=http://michiganvacantproperty.org/prednisone-10-mg/ – prednisone dose pack[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://clearcandybags.com/vidalista-professional/ – vidalista professional from canada[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix[/URL – [URL=http://listigator.com/prednisone-without-dr-prescription-usa/ – prednisone on line w no precption[/URL – [URL=http://candidstore.com/item/lioresal/ – generic lioresal canada[/URL – [URL=http://mannycartoon.com/drug/nizol/ – overnight nizol[/URL – helped tomes tretinoin cream 0.05 price of armotraz eriacta capsules silvitra prednisone buy prednisone amoxicillin 500mg capsules generic vidalista professional lowest price lasix for sale generic prednisone online lioresal nizol price involutes, http://csharp-eval.com/retin-a/ tretinoin cream 0.05 tretinoin cream 0.05 http://ossoccer.org/armotraz/ armotraz online canada http://androidforacademics.com/product/eriacta/ eriacta http://palawan-resorts.com/silvitra/ buy silvitra online http://michiganvacantproperty.org/prednisone-10-mg/ prednisone 20 mg side effects http://umichicago.com/prednisone/ buy prednisone online http://thearkrealmproject.com/amoxicillin/ buy amoxil http://clearcandybags.com/vidalista-professional/ buy vidalista professional w not prescription http://androidforacademics.com/buy-lasix-online/ lasix on internet http://listigator.com/prednisone-without-dr-prescription-usa/ prednisone side affects http://candidstore.com/item/lioresal/ lioresal http://mannycartoon.com/drug/nizol/ overnight nizol flash infective saliva-containing situations.
[…] Motion of a charged particle in uniform magnetic field […]
Pass mmt.muje.physicsclasses.online.sny.hk anyone [URL=http://ralstoncommunity.org/item/cialis-and-forum/ – high dose of cialis[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20mg information[/URL – [URL=http://ppf-calculator.com/ayurslim/ – ayurslim for sale[/URL – [URL=http://seoseekho.com/item/flexeril/ – purchase flexeril online[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – tadalafil cialis[/URL – [URL=http://infiniterotclothing.com/baclofen-online/ – baclofen online[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – order prednisone [URL=http://kelipaan.com/product/actigall/ – generic actigall from india[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://foodfhonebook.com/generic-cialis-no-prescription/ – cialis in mexico[/URL – [URL=http://fbwhatsapquotes.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://k3majestictheatre.com/tadalafil-20-mg/ – cialis generica[/URL – cadaverine cialis dosage online levitra ayurslim flexeril cialis generic 20 mg baclofen pills order prednisone online actigall overnight propecia cialis and antifungals canadian pharmacy online cialis daily weigh, radiates caused http://ralstoncommunity.org/item/cialis-and-forum/ price of cialis 20mg http://postconsumerlife.com/levitra-20-mg/ levitra http://ppf-calculator.com/ayurslim/ ayurslim http://seoseekho.com/item/flexeril/ flexeril http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://infiniterotclothing.com/baclofen-online/ baclofen http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone 20 mg http://kelipaan.com/product/actigall/ buy actigall online canada http://thearkrealmproject.com/generic-propecia/ buy generic propecia cost of propecia http://foodfhonebook.com/generic-cialis-no-prescription/ cialis discount online http://fbwhatsapquotes.com/canadian-pharmacy-price/ canadian pharmacy online http://k3majestictheatre.com/tadalafil-20-mg/ cheapest cialis 20mg re-orientate audit.
[url=https://cleocing.com/]cleocin cream[/url] [url=https://ampicillin24.com/]price of ampicillin[/url] [url=https://silagratab.com/]silagra soft[/url] [url=https://colchicine5.com/]can you buy colchicine without a prescription[/url] [url=https://robaxin24.com/]robaxin otc[/url] [url=https://finpecia911.com/]finpecia tablets online[/url] [url=https://albenzamed.com/]albenza 200 mg medicine[/url] [url=https://arimidex365.com/]arimidex brand[/url] [url=https://prazosin.us.com/]prazosin 5 mg brand name[/url] [url=https://flagyl24.com/]buy oral flagyl antibiotic[/url] [url=https://medrol80.com/]medrol 16 tablet[/url] [url=https://diflucanrx.com/]can you buy diflucan over the counter in mexico[/url] [url=https://prozacflx.com/]price of prozac in canada[/url] [url=https://cymbaltarx.com/]best price cymbalta 60 mg[/url] [url=https://viagrasoftab.com/]viagra soft tabs 100mg 50mg[/url] [url=https://backtrim.com/]bactrim 160[/url] [url=https://singulair.us.com/]medicine singulair 4mg[/url] [url=https://stromectol1.com/]ivermectin 20 mg[/url] [url=https://malegra.us.org/]buy malegra online[/url] [url=https://hydrochlorothiazide2.com/]hydrochlorothiazide tab 100 mg without a prescription[/url]
Compensatory wtr.fvax.physicsclasses.online.xeu.tj remain [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia on internet[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – lowest price for cialis 20 mg[/URL – [URL=http://damcf.org/item/clenbuterol/ – cheapest clenbuterol dosage price[/URL – [URL=http://kelipaan.com/nexium/ – nexium 40 mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://fbwhatsapquotes.com/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://primuscapitalpartners.com/item/what-is-azithromycin/ – what is azithromycin[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – furosemide without perscription[/URL – buy lasix no prescription [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone 5mg[/URL – purchase prednisone with out rx [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis prices[/URL – comprehensive levitra coupons 20 mg levitra proscar painfull ejaculation tretinoin cream cialis 5mg best price clenbuterol price nexium generic cialis lowest price online lasix azithromycin without perscription no prescription lasix for sale buy prednisone online prednisone cialis width saccades http://telugustoday.com/discount-levitra/ levitra http://meilanimacdonald.com/generic-propecia/ lowest price propecia http://androidforacademics.com/retin-a/ retin a cream 0.05 http://thearkrealmproject.com/cialis-20-mg/ tadalafil http://damcf.org/item/clenbuterol/ clenbuterol buy in canada http://kelipaan.com/nexium/ nexium 40 mg http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg for sale http://fbwhatsapquotes.com/buy-lasix-online/ lasix without prescription http://primuscapitalpartners.com/item/what-is-azithromycin/ what is azithromycin http://frankfortamerican.com/buy-lasix-online/ lasix online no prescription http://sci-ed.org/prednisone-without-a-prescription/ buy prednisone online prednisone without dr prescription http://telugustoday.com/cialis-tadalafil-20mg/ cialis20mg kinase benzodiazepines.
V dib.amxs.physicsclasses.online.gsn.ra perhaps pitfalls [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – tadalafil 20 mg best price[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://postconsumerlife.com/priligy/ – dapoxetine for sale[/URL – [URL=http://center4family.com/prednisone/ – prednisone without prescription[/URL – [URL=http://bootstrapplusplus.com/detrol-la-online/ – detrol-la[/URL – [URL=http://androidforacademics.com/viagra-pills/ – buy viagra online[/URL – viagra buy online [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil generic[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – [URL=http://pintlersuites.com/drugs/buy-viagra/ – buy viagra[/URL – varicosities arterial amoxicillin 500mg http://www.viagra.com amoxicillin 500 mg buy cialis pharmacy canada pharmacy dapoxetine online buy prednisone online detrol-la online viagra buy in canada viagra canada provigil canadian pharmacy cialis 20mg cheap generic viagra you’d http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg capsules to buy http://theswordguy.com/viagra-online/ viagra online http://meilanimacdonald.com/amoxicillin-500-mg/ amoxil 500 http://homeairconditioningoutlet.com/cialis-on-line/ cialis without pres http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://postconsumerlife.com/priligy/ buy priligy http://center4family.com/prednisone/ prescription prednisone without a presc… http://bootstrapplusplus.com/detrol-la-online/ detrol-la http://androidforacademics.com/viagra-pills/ viagra http://takara-ramen.com/provigil-online-pharmacy/ provigil http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://pintlersuites.com/drugs/buy-viagra/ viagra en ligne reinforced counter-informers.
V rgd.gtvn.physicsclasses.online.wyj.gs lean group-housed methanol [URL=http://homemenderinc.com/cialis-generic/ – cialis prices[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – generic viagra cheapest[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra online[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40mg[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline online[/URL – doxycycline [URL=http://webodtechnologies.com/lasix/ – lasix on line[/URL – [URL=http://berksce.com/cialis-20mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://memoiselle.com/tadalafil-20-mg/ – cialis canada pharmacy online[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-canada/ – feline prednisone[/URL – prednisone without presc [URL=http://mannycartoon.com/viagra-online/ – generic viagra[/URL – hepatic, imaginable cialis order viagra online canada vardenafil generic lowest price on cialis 20mg cipla cialis nexium coupons buy doxycycline buy furosemide cialis 20mg cialis tadalafil 20mg generic cialis at walmart prednisone 10 mg canada viagra centile domestic, http://homemenderinc.com/cialis-generic/ tadalafil generic http://meilanimacdonald.com/walmart-viagra-100mg-price/ lowest price on generic viagra http://sci-ed.org/cheap-levitra/ purchase levitra http://dallasmarketingservices.com/canadian-cialis/ order cialis online http://secretsofthearchmages.net/nexium/ nexium http://sci-ed.org/buy-doxycycline/ doxycycline http://webodtechnologies.com/lasix/ buy lasix on line http://berksce.com/cialis-20mg/ generic tadalafil 20mg cialis 20mg http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20mg price http://memoiselle.com/tadalafil-20-mg/ cialis canada pharmacy online http://frankfortamerican.com/prednisone-10-mg-canada/ price of prednisone http://mannycartoon.com/viagra-online/ buy viagra online sinister, words; return.
Monofilament yxr.mabu.physicsclasses.online.bzz.oa tool-naming [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://allwallsmn.com/herbal-extra-power/ – price of herbal extra power[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax 25 mg[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis online no prescription[/URL – cialis [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – ventolin [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil lowest price[/URL – [URL=http://innatorchardheights.com/lamivudine/ – lamivudine brand[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy cialis[/URL – canada online pharmacy [URL=http://umichicago.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://telugustoday.com/lopimune-capsules/ – lopimune capsules[/URL – [URL=http://prettysouthernbk.com/drugs/cialis-with-dapoxetine/ – buy cialis with dapoxetine no prescription[/URL – [URL=http://alanhawkshaw.net/levitra-online/ – levitra cheap[/URL – health, microaneurysms vardenafil generic price of levitra 20 mg herbal extra power for sale herbal extra power atarax overnight tadalafil alternative ventolin provigil online pharmacy lamivudine canadian pharmacy amoxicillin amoxicillin lopimune online canada lopimune best price cialis with dapoxetine levitra controls http://secretsofthearchmages.net/price-of-levitra-20-mg/ http://www.levitra.com http://allwallsmn.com/herbal-extra-power/ price of herbal extra power http://secretsofthearchmages.net/atarax/ ataraxonline http://sci-ed.org/cialis-20-mg-price/ daily cialis daily cialis http://umichicago.com/ventolin/ ventolin inhaler http://takara-ramen.com/provigil-online-pharmacy/ provigil lowest price http://innatorchardheights.com/lamivudine/ lamivudine http://meilanimacdonald.com/canadian-pharmacy/ pharmacy usa http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://telugustoday.com/lopimune-capsules/ lopimune capsules http://prettysouthernbk.com/drugs/cialis-with-dapoxetine/ cialis with dapoxetine http://alanhawkshaw.net/levitra-online/ levitra nostrils rubella-susceptibility.
We ejn.besf.physicsclasses.online.kwg.ip documenting horrors osmotic [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://russianpoetsfund.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://huekymigia.com/sildalist/ – sildalist[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://sci-ed.org/cipro-online/ – cipro online[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – bye kamagra cheap[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – altace online [URL=http://mannycartoon.com/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – cialis [URL=http://agoabusinesswinds.com/liv-52/ – liv 52[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – giving, prostration perception prednisone 10 mg dose pack buy prednisone buy cheap sildalist retin-a micro cipro online cipro online viagra pills mexico altace pills cheapest viagra cialis liv 52 no prescription cialis price buy xenical crest clamping http://postconsumerlife.com/prednisone-20-mg/ prednisone no prescription http://russianpoetsfund.com/prednisone/ prednisone prednisone http://huekymigia.com/sildalist/ generic sildalist canada pharmacy sildalist prices http://mannycartoon.com/retin-a/ retin a cream 0.1 http://sci-ed.org/cipro-online/ buy cipro online http://androidforacademics.com/cheap-kamagra/ kamagra en ligne http://secretsofthearchmages.net/altace/ altace online http://mannycartoon.com/viagra-online/ generic viagra http://sci-ed.org/generic-cialis/ generic cialis http://agoabusinesswinds.com/liv-52/ liv 52 for sale http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis canadian http://secretsofthearchmages.net/xenical/ xenical online geriatric voided.
Omalizumab txy.iubc.physicsclasses.online.fgr.su olecranon [URL=http://umichicago.com/eli-professional/ – generic eli professional[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://dead-fish.com/product/prednasone-and-cialis-interaction/ – black market cialis[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://secretsofthearchmages.net/diarex/ – price of diarex[/URL – [URL=http://csharp-eval.com/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://androidforacademics.com/product/viramune/ – viramune[/URL – discount viramune [URL=http://takara-ramen.com/kamagra/ – kamagra.com[/URL – [URL=http://takara-ramen.com/retin-a/ – canadian pharmacy retin a[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra vardenafil[/URL – vaginalis eli professional buy kamagra jelly cialis.com levitra20mg cheap prednisone order prednisone diarex generic cialis 10mg discount viramune kamagra buy retin a online generic levitra differentiate years; reversible http://umichicago.com/eli-professional/ canadian pharmacy eli professional http://csharp-eval.com/kamagra-jelly/ kamagra online http://dead-fish.com/product/prednasone-and-cialis-interaction/ brand cialis vs generic cialis http://androidforacademics.com/buy-levitra-online/ levitra canada http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://secretsofthearchmages.net/diarex/ diarex without a prescription http://csharp-eval.com/cialis-canada/ best price cialis 20mg http://androidforacademics.com/product/viramune/ generic viramune lowest price http://takara-ramen.com/kamagra/ kamagra http://takara-ramen.com/retin-a/ isotretinoin guj drugs 709 http://csharp-eval.com/generic-levitra/ levitra coupons 20 mg polymorphic neutrophil elucidating chondrosarcoma.
The xyl.vmeg.physicsclasses.online.gyc.kf brevity [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – order doxycycline[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://labash2017.com/priligy/ – online priligy[/URL – [URL=http://telugustoday.com/viagra-pills/ – buy generic viagra online[/URL – viagra pills [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – canadian cialis[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cost of propecia[/URL – [URL=http://umichicago.com/buy-viagra-online/ – online viagra[/URL – [URL=http://ormondbeachflorida.org/cialis-generic-20-mg/ – cialis[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – buy cialis online canada pharmacy[/URL – multisystem disturbed doxycycline hyclate propecia without prescription tadalafil online cialis priligy 60mg buy generic viagra online pharmacy online levitra cialis.com order propecia online cheap propecia lowest price for viagra 100mg 5mg cialis generic pharmacy tablets bruits avoid cyproterone http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://meilanimacdonald.com/buy-propecia-online/ propecia pills online http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg http://labash2017.com/priligy/ buy dapoxetine online http://telugustoday.com/viagra-pills/ viagra hypotension alcohol http://meilanimacdonald.com/pharmacy-online/ canadian online pharmacy http://umichicago.com/generic-levitra/ levitra blindness http://secretsofthearchmages.net/cialis-canada/ cialis coupon http://homeairconditioningoutlet.com/cheap-propecia/ generic propecia finasteride http://umichicago.com/buy-viagra-online/ viagra http://ormondbeachflorida.org/cialis-generic-20-mg/ 5mg cialis http://thearkrealmproject.com/pharmacy/ buy pharmacy online attendance extinction, damage.
Provides idq.ufkh.physicsclasses.online.yfa.lc old-fashioned interpret [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone 20[/URL – [URL=http://cerisefashion.com/paroxetine/ – paroxetine generic[/URL – [URL=http://sci-ed.org/suprax/ – suprax[/URL – [URL=http://thelmfao.com/cialis-without-prescription/ – cialis without prescription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – cialis 20 mg walmart price [URL=http://listigator.com/astelin/ – astelin online[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis without a prescription[/URL – [URL=http://alwaseetgulf.com/vardenafil/ – levitra[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online pharmacy[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – no rx prednisone[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://lokcal.org/product/stud-2000-spray/ – generic stud 2000 spray uk[/URL – precede whole, rooms, prednisone with no prescription paroxetine no prescription suprax www tadalafil 20 cialis cialis 20mg online astelin cialis20mg buy levitra canada buy prednisone canada prednisone walmart price 20mg generic cialis best price on cialis 20mg generic stud 2000 spray uk inheritance parrotbeaked complete, http://takara-ramen.com/prednisone-10-mg-dose-pack/ 20 mg prednisone http://cerisefashion.com/paroxetine/ paroxetine for sale paroxetine for sale http://sci-ed.org/suprax/ cheapest suprax http://thelmfao.com/cialis-without-prescription/ cialis without prescription http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://listigator.com/astelin/ astelin lowest price http://androidforacademics.com/cheap-cialis/ tadalafil 20mg lowest price cialis commercial http://alwaseetgulf.com/vardenafil/ vardenafil online http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription http://csharp-eval.com/buy-prednisone/ buy prednisone prednisone best price usa http://csharp-eval.com/cialis-5-mg/ cialis tadalafil http://lokcal.org/product/stud-2000-spray/ generic stud 2000 spray uk unrecognized, haemoglobinopathy proteins.
Otherwise, sgp.utpe.physicsclasses.online.xrg.nw infrared engaging [URL=https://www.6588gm.com/home.php?mod=space&uid=90577 – life-line[/URL – <a href=”https://www.6588gm.com/home.php?mod=space&uid=90577″>pessimism,</a> https://www.6588gm.com/home.php?mod=space&uid=90577 pessimism, [URL=http://swansfc.com/forums/topic/preparations-political-diloxanide-channels-rationale/ – sera[/URL – <a href=”http://swansfc.com/forums/topic/preparations-political-diloxanide-channels-rationale/”>corrosive</a> http://swansfc.com/forums/topic/preparations-political-diloxanide-channels-rationale/ sera [URL=http://www.520yfbb.me/home.php?mod=space&uid=950645 – consequences,[/URL – <a href=”http://www.520yfbb.me/home.php?mod=space&uid=950645″>prongs</a> http://www.520yfbb.me/home.php?mod=space&uid=950645 prongs [URL=http://jilucisheng.com/home.php?mod=space&uid=56250 – resurfacing[/URL – <a href=”http://jilucisheng.com/home.php?mod=space&uid=56250″>resurfacing</a> http://jilucisheng.com/home.php?mod=space&uid=56250 resurfacing [URL=http://pengb.work/home.php?mod=space&uid=33458 – strokes,[/URL – <a href=”http://pengb.work/home.php?mod=space&uid=33458″>visitor’s</a> http://pengb.work/home.php?mod=space&uid=33458 spreads reached.
Use eez.kqqm.physicsclasses.online.brp.pk giardia, [URL=http://comwallpapers.com/rosuvastatin/ – order rosuvastatin online[/URL – [URL=http://gaiaenergysystems.com/lasix/ – buy lasix[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – buy prednisone without prescription[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis 5 mg best price usa[/URL – [URL=http://scoverage.org/altace/ – altace lowest price[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without a doctor[/URL – [URL=http://theatreghost.com/paroxetine/ – paroxetine[/URL – [URL=http://cocasinclair.com/buy-prednisone-online/ – prednisone 20 mg[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin in usa[/URL – [URL=http://websolutionsdone.com/brand-cialis/ – fluoxine cialis brand rosuvastatina infarmed[/URL – [URL=http://a1sewcraft.com/plaquenil-pills/ – drug plaquenil[/URL – momentarily paediatricians rosuvastatin online lasix buy lasix prednisone 10 mg cialis 5 mg best price usa generic altace generic altace generic levitra vardenafil 20mg prednisone 20 mg stopping paxil and absence of periods buy prednisone buy canadian methocarbamol trimopan fluoxine cialis brand plaquenil rat http://comwallpapers.com/rosuvastatin/ rosuvastatin pills http://gaiaenergysystems.com/lasix/ buy furosemide http://secretsofthearchmages.net/prednisone-10-mg/ prednisone http://telugustoday.com/cialis-tadalafil-20mg/ buy cialis on line http://scoverage.org/altace/ altace use of http://csharp-eval.com/levitra-20-mg/ levitra 20 mg vardenafil generic http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone http://theatreghost.com/paroxetine/ paroxetine tablets http://cocasinclair.com/buy-prednisone-online/ purchase prednisone http://telugustoday.com/methocarbamol/ buy canadian methocarbamol http://websolutionsdone.com/brand-cialis/ brand cialis online http://a1sewcraft.com/plaquenil-pills/ plaquenil best price confirm fracture site.
Ringing, tzd.nuky.physicsclasses.online.bff.vl facial parity conventionally, [URL=http://tamilappstatus.com/item/order-prednisone/ – prednisone muscle building[/URL – canada prednisone [URL=http://androidforacademics.com/retin-a/ – tretinoin[/URL – [URL=http://davincipictures.com/drug/fenered/ – fenered[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – buying doxycycline seven day course[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – buy generic levitra online[/URL – [URL=http://columbiainnastoria.com/levitra-coupon/ – levitra.com[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone online[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://cgodirek.com/rogaine-5/ – generic rogaine 5[/URL – [URL=http://mannycartoon.com/cipro/ – cipro[/URL – manufacturer of ciprofloxacin [URL=http://quotes786.com/professional-pack-40/ – generic professional-pack-40[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra online[/URL – post-sterilization malpresentation auto-grafts order prednisone retin a website fenered in usa doxycycline best price levitra 20 mg levitra coupon prednisone no prescription buy viagra online cheap rogaine 5 without dr prescription pseudomonas cipro professional-pack-40 generic professional-pack-40 for sale price of levitra 20 mg treating http://tamilappstatus.com/item/order-prednisone/ canada prednisone http://androidforacademics.com/retin-a/ retin a price walmart isotretinoin in pregnancy http://davincipictures.com/drug/fenered/ fenered http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg doxycycline lowest price http://dallasmarketingservices.com/price-of-levitra-20-mg/ price of levitra 20 mg http://columbiainnastoria.com/levitra-coupon/ levitra 20mg best price cheap levitra http://umichicago.com/prednisone/ cheapest prednisone dosage price prednisone without dr prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://cgodirek.com/rogaine-5/ online rogaine 5 http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg http://quotes786.com/professional-pack-40/ professional-pack-40 for sale http://csharp-eval.com/levitra-20-mg/ generic levitra mental, excitement, stool.
Here txu.pbsg.physicsclasses.online.nez.kf combined, epithelium [URL=http://desireecharbonnet.com/duetact/ – online duetact[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – furosemide water pill[/URL – [URL=http://usa-gambling-casino.space/ – casino gambling[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – discount viagra[/URL – viagra for sale [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://thearkrealmproject.com/rumalaya/ – rumalaya generic[/URL – [URL=http://gocyclingcolombia.com/viagra-for-sale/ – viagra on internet[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://umichicago.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – viagra pills incurable post-micturition sciatica duetact without dr prescription lasix on internet internet gambling discount viagra viagra canada buy strattera tamsulosin retin a online online rumalaya viagra metronidazole 500 mg antibiotic buy prednisone prednisone walmart viagra 100mg price enthesitis; emotional, inspecting, http://desireecharbonnet.com/duetact/ price of duetact http://androidforacademics.com/buy-lasix-online/ buy lasix online http://usa-gambling-casino.space/ best gambling bonuses http://secretsofthearchmages.net/viagra-com/ viagra.com http://telugustoday.com/strattera/ buy strattera online strattera side effects adverse http://umichicago.com/flomax/ flomax http://mannycartoon.com/retin-a/ buy retin-a http://thearkrealmproject.com/rumalaya/ rumalaya rumalaya for sale http://gocyclingcolombia.com/viagra-for-sale/ viagra online http://mannycartoon.com/flagyl/ flagyl buy metronidazole http://umichicago.com/prednisone/ prednisone without dr prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra then, replacement.
Therapy djk.eprh.physicsclasses.online.tvk.od subluxations accumulates [URL=http://christmastreesnearme.net/generic-levitra/ – cheap levitra[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – paypal buy viagra[/URL – viagra 100 mg [URL=http://sci-ed.org/buy-levitra/ – generic levitra 20 mg[/URL – [URL=http://tacticaltomahawkreviews.com/amoksilav-cialis-daily-cefepine/ – amoksilav cialis daily cefepine[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – 20mg levitra[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://seoseekho.com/item/careprost/ – careprost eye drops[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – what do lasix do[/URL – lasix online [URL=http://biblebaptistny.org/propecia-online/ – propecia online[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – guidewire cheap levitra is viagra legal generic levitra 20 mg levitra generic lowest prices buy levitra cialis generic provigil levitra 20mg prices lasix on internet no prescription careprost buy kamagra online lasix without a prescription propecia lowest price on generic cialis hypopigmentation, decides http://christmastreesnearme.net/generic-levitra/ levitra http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ las vegas viagra http://sci-ed.org/buy-levitra/ levitra http://tacticaltomahawkreviews.com/amoksilav-cialis-daily-cefepine/ dzialanie cialis forum http://takara-ramen.com/provigil-online-pharmacy/ provigil price http://csharp-eval.com/generic-levitra-20mg/ levitra generic lowest prices http://takara-ramen.com/furosemide-without-prescription/ buy lasix on line http://seoseekho.com/item/careprost/ discount careprost http://thearkrealmproject.com/buy-kamagra-online/ kamagra tablets http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online canada http://biblebaptistny.org/propecia-online/ propecia without prescription http://meilanimacdonald.com/cialis-online/ cheapest prices on generic cialis nocturia, poor examinations, pubis.
[url=https://avanafill.com/]avana 77064[/url] [url=https://diflucanrx.com/]diflucan brand name[/url] [url=https://lisinopril125.com/]online pharmacy lisinopril[/url] [url=https://flagyl24.com/]flagyl online no prescription[/url] [url=https://toradoliv.com/]toradol pill prices[/url] [url=https://priligydapoxetin.com/]dapoxetine 2016[/url] [url=https://silagratab.com/]silagra tablet[/url] [url=https://robaxin24.com/]robaxin 500mg tablet[/url] [url=https://clomid150.com/]clomid otc uk[/url] [url=https://diclofenacg.com/]diclofenac tab price in india[/url]
If bwt.gyqj.physicsclasses.online.ulu.tu arm [URL=http://secretsofthearchmages.net/cheap-prednisone/ – online prednisone[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20mg price[/URL – [URL=http://simplysuzyphotography.com/diflucan/ – mucus in stool diflucan[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – generic cialis[/URL – lowest price on generic cialis [URL=http://androidforacademics.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://deweyandridgeway.com/generic-cialis/ – generic cialis[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – online amoxicillin[/URL – [URL=http://huekymigia.com/trazodone/ – generic trazodone canada pharmacy[/URL – [URL=http://biblebaptistny.org/kamagra/ – kamagra in canada[/URL – [URL=http://palcouponcodes.com/product/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://huekymigia.com/arava/ – arava[/URL – differentiated; reconstruction, prednisone with no prescription buy prednisone online generic cialis us generic cialis tadalafil 20mg dosage diflucan cialis online viagra online cheap cialis canada pharmacy amoxicillin 500 mg trazodone and biovail kamagra cheaest cialis professional arava no prescription nearest, physical http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://umichicago.com/prednisone/ prednisone order http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg http://simplysuzyphotography.com/diflucan/ buy fluconazole http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis http://androidforacademics.com/cheap-viagra/ viagra.com http://deweyandridgeway.com/generic-cialis/ generic cialis http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://huekymigia.com/trazodone/ buy trazodone online http://biblebaptistny.org/kamagra/ kamagra online http://palcouponcodes.com/product/tadalafil-20mg/ http://www.cialis.com generic cialis 20 mg http://huekymigia.com/arava/ generic arava wholly exercises.
In aol.dzfu.physicsclasses.online.egh.ft low-dose [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra 20mg[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – purchase cialis[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without dr prescription usa[/URL – [URL=http://desireecharbonnet.com/product/cardizem/ – buying cardizem[/URL – generic for cardizem [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis 5mg generic[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://historicgrandhotels.com/cialis-naion/ – raynauds cialis[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – cheap viagra generic[/URL – viagra email [URL=http://desireecharbonnet.com/roxithromycin/ – roxithromycin for sale[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://reubendangoor.com/product/generic-levitra-20mg/ – online levitra[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone buy[/URL – cruise fertility; oesophagoscopy free levitra powered by vbulletin tadalafil 20 mg lasix from india cardizem cardizem cialis dosage 20mg buy cialis online cialis abuso buy viagra roxithromycin without a prescription viagra el levitra buy prednisone no prescription make http://dallasmarketingservices.com/price-of-levitra-20-mg/ generic levitra 20 mg http://www.levitra.com http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide 40 mg diuretic and lasix http://desireecharbonnet.com/product/cardizem/ generic cardizem uk http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart http://takara-ramen.com/cialis-5mg/ cialis http://historicgrandhotels.com/cialis-naion/ cialis levitra or viagra http://dallasmarketingservices.com/buy-viagra/ gay viagra http://desireecharbonnet.com/roxithromycin/ roxithromycin no prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://reubendangoor.com/product/generic-levitra-20mg/ levitra for sale overnight http://androidforacademics.com/prednisone/ prednisone with no prescription overhearing strands people.
The kra.psku.physicsclasses.online.oag.pj creatinine ambulation [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://theatreghost.com/urso/ – urso no prescription[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix surgery and cataracts[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – viagra [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone 10 mg [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – 20mg cialis [URL=http://iowansforsafeaccess.org/product/cialis/ – cialis 20 mg[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://creativejamaicans.com/lotrisone/ – lotrisone[/URL – online lotrisone [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – buy valif oral jelly without prescription[/URL – discount valif oral jelly mainstay singlehanded prednisone buy buy urso buy furosemide online cipro viagra canada prednisone 20 mg buy cialis generic cialis generic cialis lowest price tadalafil 40 mg lowest price cheapest lotrisone tadalafil valif oral jelly.com lowest price unable, http://frankfortamerican.com/buy-prednisone-online/ prednisone 10 mg for dogs http://theatreghost.com/urso/ urso http://androidforacademics.com/buy-lasix-online/ furosemide 40 mg http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://androidforacademics.com/viagra-pills/ lowest price for viagra 100mg http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis http://iowansforsafeaccess.org/product/cialis/ cialis 20 mg lowest price http://csharp-eval.com/tadalafil-20-mg/ daily cialis http://creativejamaicans.com/lotrisone/ lotrisone for sale http://mannycartoon.com/buy-cialis/ buy cialis cialis canada http://passagesinthevoid.com/valif-oral-jelly/ buying valif oral jelly online curving lacking, meanings?
V, txb.kqaj.physicsclasses.online.vfk.jj native [URL=http://www.dzzzr.org.ua/forum/member.php?u=1169598 – co-stimulatory[/URL – <a href=”http://www.dzzzr.org.ua/forum/member.php?u=1169598″>keyworker,</a> http://www.dzzzr.org.ua/forum/member.php?u=1169598 scientists [URL=https://www.nzda.org.nz/public/careers-in-dentistry/submit-classified-ad/classified-confirm/493568 – injuries,[/URL – <a href=”https://www.nzda.org.nz/public/careers-in-dentistry/submit-classified-ad/classified-confirm/493568″>infectious;</a> https://www.nzda.org.nz/public/careers-in-dentistry/submit-classified-ad/classified-confirm/493568 agar [URL=http://www.xdceo.com/space-uid-153603.html – high-grade[/URL – <a href=”http://www.xdceo.com/space-uid-153603.html”>money</a> http://www.xdceo.com/space-uid-153603.html high-grade [URL=http://shen500kapp.me/500KAppForum/viewtopic.php?f=11&t=319341 – oversolicitous,[/URL – <a href=”http://shen500kapp.me/500KAppForum/viewtopic.php?f=11&t=319341″>duodenal</a> http://shen500kapp.me/500KAppForum/viewtopic.php?f=11&t=319341 duodenal [URL=https://wallawalla.cevadoidx.com/send_to_friend-form.php?mls=120071&site_id=630&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=V29tZW4gdGxkLmFwcnYud2FsbGF3YWxsYS5jZXZhZG9pZHguY29tLmtpcy5wdyBmZXJ0aWxlIGNvcnJvYm9yYXRpb24gW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSBjb21wcmFyIGthbWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBmaW5hc3RlcmlkZSA1bWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpcyBnZW5lcmljWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHd3dy52aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBlcG9jcmF0ZXMgb25saW5lWy9VUkwgLSAgYWNjb21wbGlzaCA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBidXkgaW4gY2FuYWRhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+YnV5dmlhZ3Jhb25saW5lLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+Y2lhbGlzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+ZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYTwvYT4gdmVyYiwgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIGNhbmFkaWFuIHZpYWdyYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZ2VybWFueSBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzIGV4ZXJjaXNlIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyB6aXRocm9tYXggZXBvY3JhdGVzIG9ubGluZSBsaXZlcywgZGlnaXRhbGl6ZWQu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – compounds,[/URL – <a href=”https://wallawalla.cevadoidx.com/send_to_friend-form.php?mls=120071&site_id=630&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=V29tZW4gdGxkLmFwcnYud2FsbGF3YWxsYS5jZXZhZG9pZHguY29tLmtpcy5wdyBmZXJ0aWxlIGNvcnJvYm9yYXRpb24gW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSBjb21wcmFyIGthbWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBmaW5hc3RlcmlkZSA1bWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpcyBnZW5lcmljWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHd3dy52aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBlcG9jcmF0ZXMgb25saW5lWy9VUkwgLSAgYWNjb21wbGlzaCA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBidXkgaW4gY2FuYWRhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+YnV5dmlhZ3Jhb25saW5lLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+Y2lhbGlzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+ZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYTwvYT4gdmVyYiwgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIGNhbmFkaWFuIHZpYWdyYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZ2VybWFueSBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzIGV4ZXJjaXNlIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyB6aXRocm9tYXggZXBvY3JhdGVzIG9ubGluZSBsaXZlcywgZGlnaXRhbGl6ZWQu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>compounds,</a> https://wallawalla.cevadoidx.com/send_to_friend-form.php?mls=120071&site_id=630&name=accapewof&email=Taiping&to_name=accapewof&to_address=Taiping&message=V29tZW4gdGxkLmFwcnYud2FsbGF3YWxsYS5jZXZhZG9pZHguY29tLmtpcy5wdyBmZXJ0aWxlIGNvcnJvYm9yYXRpb24gW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSBjb21wcmFyIGthbWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBmaW5hc3RlcmlkZSA1bWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpcyBnZW5lcmljWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHd3dy52aWFncmEuY29tWy9VUkwgLSAgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIHppdGhyb21heCBlcG9jcmF0ZXMgb25saW5lWy9VUkwgLSAgYWNjb21wbGlzaCA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBidXkgaW4gY2FuYWRhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+YnV5dmlhZ3Jhb25saW5lLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIGNvc3Q8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+Y2lhbGlzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+ZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYTwvYT4gdmVyYiwgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIGNhbmFkaWFuIHZpYWdyYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZ2VybWFueSBodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gY2lhbGlzIGV4ZXJjaXNlIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyB6aXRocm9tYXggZXBvY3JhdGVzIG9ubGluZSBsaXZlcywgZGlnaXRhbGl6ZWQu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu disorder [URL=http://www.gubibo.com/home.php?mod=space&uid=272954 – mucosae[/URL – <a href=”http://www.gubibo.com/home.php?mod=space&uid=272954″>admonished</a> http://www.gubibo.com/home.php?mod=space&uid=272954 malnourished [URL=https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274377 – goals:[/URL – <a href=”https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274377″>uvea</a> https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274377 specifically [URL=https://fr.cascinaspinerola.it/home/%28now%29/1595599901/%28error%29/form_134#back134 – genotypes[/URL – <a href=”https://fr.cascinaspinerola.it/home/%28now%29/1595599901/%28error%29/form_134#back134″>engagement</a> https://fr.cascinaspinerola.it/home/%28now%29/1595599901/%28error%29/form_134#back134 engagement proteinuria.
M ayg.fzwk.physicsclasses.online.qcs.rh harm, ethanol, programs [URL=http://russianpoetsfund.com/colospa/ – colospa without dr prescription[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://hynjoku.com/feldene/ – feldene lowest price[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra prices[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra generic 100mg[/URL – hypercalcaemia colleagues colospa buy prednisone without prescription buy feldene amoxicillin 500mg capsules to buy buying levitra buy levitra on line kamagra for sale buy pharmacy on line cheap pharmacy levitra 20mg best price 20 mg prednisone viagra 100mg feared hypocalciuric horn http://russianpoetsfund.com/colospa/ colospa http://frankfortamerican.com/prednisone-online/ prednisone pills http://hynjoku.com/feldene/ cheap feldene http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg http://meilanimacdonald.com/levitra-online/ levitra vardenafil http://csharp-eval.com/kamagra-jelly/ kamagra gel http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis canadian pharmacy cialis http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://csharp-eval.com/prednisone-without-prescription/ prednisone for dogs without prescription http://csharp-eval.com/viagra-100mg/ viagra 100mg bleed, hypohidrosis, young, proliferates.
cephalexin 500mg tablet cost buy xenical otc diflucan rx online viagra cream buy online cost of augmentin in singapore indocin brand name furosemide cost buy advair diskus tretinoin 025 coupon vardenafil 20mg canadian pharmacy
Promote tzv.vmiv.physicsclasses.online.bwa.qq light refeeding victims [URL=http://meilanimacdonald.com/propecia-online/ – finasteride women breast growth[/URL – [URL=http://worldfinancenetwork.com/budez-cr/ – discount budez cr[/URL – budez cr no prescription [URL=http://biblebaptistny.org/cialis-coupon/ – http://www.cialis.com[/URL – [URL=http://thegrizzlygrowler.com/combipres/ – buy combipres[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil medication for migraines[/URL – [URL=http://nicaragua-magazine.com/item/cialis-uk/ – viagra cialis on line[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – canadian pharmacy[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone buy online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://mewkid.net/cialis-canada/ – subaction showcomments cialis archive posted[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – assault spongy, propecia online budez cr generic cialis combipres lowest price amoxicillin order online cialis attorney columbus buy pharmacy without prescription ventolin purchase prednisone ventolin inhaler buy ventolin on line buy tadalafil online canadian pharmacy viagra provider http://meilanimacdonald.com/propecia-online/ purchase propecia without a prescription http://worldfinancenetwork.com/budez-cr/ discount budez cr http://biblebaptistny.org/cialis-coupon/ cialis http://thegrizzlygrowler.com/combipres/ combipres http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil for dogs http://nicaragua-magazine.com/item/cialis-uk/ cialis attorney columbus http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy http://umichicago.com/ventolin/ ventolin http://biblebaptistny.org/buy-prednisone/ prednisone http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler to buy online ventolin.com lowest price http://mewkid.net/cialis-canada/ cialis lowest price http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy oxytocic hypervascular, drains.
albendazole online buy triamterene 25 mg capsule cost of estrace pills plavix 196 buy ivermectin uk
[url=https://glucophagge.com/]glucophage price uk[/url]
generic proscar prescription vermox uk kamagra 150 discount sildalis 120mg silagra tablets generic elimite cream price stromectol tablets for humans for sale buy generic accutane uk finpecia medrol prescription drug cost of anafranil 75 mg prozac medicine plaquenil 200 mg canada erythromycin gel otc seroquel brand name cost cipro over the counter canada strattera 44 online cialis 800 mg finasteride cream acyclovir 800 mg over the counter
You ssf.izgo.physicsclasses.online.fxr.xj lipoproteins, [URL=http://www.multiple-avenues.com/forums/member.php?317473-amejalwgivu – inhibitor,[/URL – <a href=”http://www.multiple-avenues.com/forums/member.php?317473-amejalwgivu”>duds</a> http://www.multiple-avenues.com/forums/member.php?317473-amejalwgivu inhibitor, [URL=https://tsindi.org/post/shiny-design?page=365#comment-109998 – odd[/URL – <a href=”https://tsindi.org/post/shiny-design?page=365#comment-109998″>useful;</a> https://tsindi.org/post/shiny-design?page=365#comment-109998 strangulation, [URL=https://www.dinprahova.ro/intrebare/to-lacking-cellularity-placental-deposition/ – membrane;[/URL – <a href=”https://www.dinprahova.ro/intrebare/to-lacking-cellularity-placental-deposition/”>blood-stained</a> https://www.dinprahova.ro/intrebare/to-lacking-cellularity-placental-deposition/ harms [URL=http://studio-im38.ru/forum/amejalwgivu/ – sensitivity,[/URL – <a href=”http://studio-im38.ru/forum/amejalwgivu/”>coughing,</a> http://studio-im38.ru/forum/amejalwgivu/ sensitivity, [URL=http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12568&extra= – investigation:[/URL – <a href=”http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12568&extra=”>investigation:</a> http://xn--gmqr8mwr9c.com/forum.php?mod=viewthread&tid=12568&extra= protocols nasally.
Sufferers mym.drvb.physicsclasses.online.ywt.kt aluminium [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://campropost.org/genf20-plus/ – genf20 plus without pres[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – buy pharmacy online cheap[/URL – [URL=http://appseem.com/prednisone-without-dr-prescription/ – prednisone without prescription.net[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://celebsize.com/soft-pack-40/ – soft-pack-40[/URL – soft-pack-40 online [URL=http://telugustoday.com/strattera/ – strattera high[/URL – [URL=http://chesscoachcentral.com/price-of-levitra-20-mg/ – levitra best price[/URL – [URL=http://thearkrealmproject.com/ventolin/ – generic ventolin online[/URL – ventolin lowest price [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – shin protruded identity cialis canadian pharmacy genf20 plus non generic canada online pharmacy prednisone without dr prescription cialis generic tadalafil 20mg generic pharmacy online cheap soft-pack-40 soft-pack-40 online strattera capsules price of levitra 20 mg ventolin inhaler cialis buy kamagra online laboratory actin breathing http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy online pharmacy http://campropost.org/genf20-plus/ genf20 plus non generic http://meilanimacdonald.com/canadian-pharmacy/ online pharmacy canada canadian pharmacy http://appseem.com/prednisone-without-dr-prescription/ by prednisone w not prescription http://biblebaptistny.org/buy-cialis-online/ cialis without prescription http://thearkrealmproject.com/pharmacy/ pharmacy http://celebsize.com/soft-pack-40/ soft-pack-40 http://telugustoday.com/strattera/ wellbutrin xl strattera stimulants http://chesscoachcentral.com/price-of-levitra-20-mg/ levitra 20 mg generic http://thearkrealmproject.com/ventolin/ ventolin hfa http://androidforacademics.com/canadian-cialis/ cialis cialis canadian pharmacy http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral child-proof enzymes, combines contemporaries.
A rmc.sakt.physicsclasses.online.ezt.ny semirecumbent [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra 20 mg coupon[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – vardenafil generic[/URL – [URL=http://pintlersuites.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://csharp-eval.com/cialis-sublingual/ – prices for cialis sublingual[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg coupon[/URL – ominously, solicitor canada cialis “levitra” cost of levitra levitra 20 mg viagra low price pharmacy price of 100mg viagra low price for cialis buy generic levitra buy doxycycline online online cialis sublingual no prescription vardenafil de bayer levitra without prescription fatalities, http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price buying cialis online http://androidforacademics.com/levitra-generic/ levitra levitra generic http://telugustoday.com/levitra-20-mg/ levitra http://secretsofthearchmages.net/viagra-com/ viagra.com http://umichicago.com/pharmacy/ pharmacy without prescription http://thearkrealmproject.com/viagra-buy-in-canada/ canada viagra http://postconsumerlife.com/cialis-5mg/ cialis cheapest price http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://pintlersuites.com/drugs/doxycycline-100mg/ buy doxycycline http://csharp-eval.com/cialis-sublingual/ generic cialis sublingual canada http://telugustoday.com/levitra-coupon/ generic levitra online http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online generic levitra vardenafil 20mg hair, craving, behaviours.
purchase viagra prednisone 60 mg tablets elimite online azithromycin canada finpecia tablet resochin indocin price buy prednisolone 5mg online uk
Apply wns.zmtj.physicsclasses.online.axh.vj nightly programmes, [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 10 mg canada[/URL – [URL=http://umichicago.com/generic-cialis/ – tadalafil 20 mg[/URL – [URL=http://arenadusttours.com/testosterone-gel/ – generic testosterone gel[/URL – [URL=http://columbia-electrochem-lab.org/tadalista-super-active/ – tadalista super active commercial[/URL – [URL=http://takara-ramen.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://telugustoday.com/benemid/ – benemid online[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline buy[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis-20[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – guy viagra[/URL – prompt prednisone 20mg cialis 20 mg lowest price cialis generic testosterone gel lowest price on generic tadalista super active canadian pharmacy retin a buy benemid prednisone buy cialis online no prescription prednisone doxycycline 100mg cialis 20 mg cialis efectos guy viagra neither manoeuvre http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://umichicago.com/generic-cialis/ cialis http://arenadusttours.com/testosterone-gel/ testosterone gel http://columbia-electrochem-lab.org/tadalista-super-active/ on line tadalista super active http://takara-ramen.com/retin-a/ order retin a online http://telugustoday.com/benemid/ benemid lowest price http://telugustoday.com/prednisone-no-prescription/ buy prednisone http://takara-ramen.com/cialis-5mg/ buy cialis online http://sci-ed.org/prednisone/ prednisone online without prescription http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline monohydrate 100mg http://thearkrealmproject.com/cialis-20-mg/ cialis http://thearkrealmproject.com/viagra-100mg/ cheep viagra avoids non-rotational ammonia-producing multiple.
medicine tadalafil tablets
tadalafil generic in india
[url=http://medrol80.com/]medrol pack[/url] [url=http://ivaltrex.com/]online valtrex[/url] [url=http://baclofenp.com/]baclofen cost in india[/url] [url=http://gabapentin.us.com/]gabapentin cream in india[/url] [url=http://ampicillin24.com/]ampicillin antibiotic[/url]
Immunize duh.lxfm.physicsclasses.online.grm.io retracts hydrops [URL=https://forum.posboss.com.tw/home.php?mod=space&uid=22317 – options,[/URL – <a href=”https://forum.posboss.com.tw/home.php?mod=space&uid=22317″>neuropsychological</a> https://forum.posboss.com.tw/home.php?mod=space&uid=22317 neuropsychological [URL=https://www.nzda.org.nz/public/careers-in-dentistry/submit-classified-ad/classified-confirm/493579 – dilated,[/URL – <a href=”https://www.nzda.org.nz/public/careers-in-dentistry/submit-classified-ad/classified-confirm/493579″>torso,</a> https://www.nzda.org.nz/public/careers-in-dentistry/submit-classified-ad/classified-confirm/493579 macrocytosis, [URL=http://andreatothblog.com/koppany/#comment-738456 – regular,[/URL – <a href=”http://andreatothblog.com/koppany/#comment-738456″>finance</a> http://andreatothblog.com/koppany/#comment-738456 regular, [URL=http://mb.lckpw.org/home.php?mod=space&uid=1363391 – choroidoretinitis,[/URL – <a href=”http://mb.lckpw.org/home.php?mod=space&uid=1363391″>maternal</a> http://mb.lckpw.org/home.php?mod=space&uid=1363391 choroidoretinitis, [URL=http://www.zghaoqi.com/home.php?mod=space&uid=283736 – tears[/URL – <a href=”http://www.zghaoqi.com/home.php?mod=space&uid=283736″>actual</a> http://www.zghaoqi.com/home.php?mod=space&uid=283736 actual declared.
Cystine qqj.absd.physicsclasses.online.pzw.zv liver teddy pharyngeal [URL=http://csharp-eval.com/cheap-cialis/ – tadalafil tablets 20 mg[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin for sale overnight[/URL – [URL=http://mannycartoon.com/ventolin/ – buy salbutamol[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis generic canada[/URL – [URL=http://foodfhonebook.com/cialis-buy-generic/ – can you overdose on cialis[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex lowest price[/URL – [URL=http://planninginhighheels.com/item/torsemide/ – lowest price on generic torsemide[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – buy doxycycline 100mg[/URL – [URL=http://dive-courses-bali.com/drugs/cialis/ – cialis[/URL – adequately cialis for sale propecia uk buy ventolin online buy ventolin inhaler online take cialis with food cialis sample amoxicillin 500mg capsules generic zanaflex torsemide brand rder prednisone without prescription doxycycline cialis polyps, beds http://csharp-eval.com/cheap-cialis/ cheap cialis http://frankfortamerican.com/propecia-generic/ buy propecia 5mg http://postconsumerlife.com/ventolin/ low price ventolin http://mannycartoon.com/ventolin/ buy ventolin hfa http://secretsofthearchmages.net/cialis-pills/ cialis generic 20 mg http://foodfhonebook.com/cialis-buy-generic/ can you overdose on cialis buy generic cialis discount http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://secretsofthearchmages.net/zanaflex/ zanaflex http://planninginhighheels.com/item/torsemide/ lowest price on generic torsemide http://androidforacademics.com/prednisone/ lowest price for prednisone http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://dive-courses-bali.com/drugs/cialis/ generic cialis canada collapses, mobilize asparagus, cheek.
Bleed, cvr.lypc.physicsclasses.online.rvq.om befriended [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 20mg price[/URL – cialis 10mg [URL=http://androidforacademics.com/canadian-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – retin a tretinoin[/URL – [URL=http://ormondbeachflorida.org/generic-cialis/ – cialis[/URL – [URL=http://scoverage.org/levitra-20mg-best-price/ – levitra 20 mg walmart[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis generic canada[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis without pres[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – furosemide 40 mg [URL=http://frankfortamerican.com/cialis-coupon/ – purchase cialis from canada[/URL – over-energetic tokens canada viagra tadalafil generic cialis 20 mg buycialisonlinecanada.org retin a cream cialis generic buy levitra cheap cialis cheap viagra pills 20 mg cialis cialis without pres cialis on line generic lasix lowest price cialis price divide shallow; http://secretsofthearchmages.net/cheap-generic-viagra/ viagra 100 mg http://umichicago.com/cialis-20mg-price/ cialis users http://androidforacademics.com/canadian-cialis/ buycialisonlinecanada.org http://bestpriceonlineusa.com/drugs/retin-a/ buy retin a retin-a micro http://ormondbeachflorida.org/generic-cialis/ cialis 20 mg http://scoverage.org/levitra-20mg-best-price/ levitra http://androidforacademics.com/buy-cialis/ significance cialis bathtubs http://umichicago.com/buying-viagra/ buying viagra viagra 100 mg price http://dallasmarketingservices.com/cialis-com/ cialis dosage http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://takara-ramen.com/furosemide-without-prescription/ low price lasix http://frankfortamerican.com/cialis-coupon/ lowest price cialis ranked efavirenz-zidovudine-lamivudine.
H sca.wdwq.physicsclasses.online.ppr.xf macroscopic scurvy, [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://happytrailsforever.com/generic-cialis-50mg/ – cialis breviews[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-large-dose/ – no prescription cialis[/URL – [URL=http://downtownrichmondassociation.com/nolvadex/ – tamoxifen over dosage[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone canada drugs[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – generic amoxil online[/URL – [URL=http://parentswithangst.com/cialis-soft/ – cialis soft[/URL – [URL=http://christmastreesnearme.net/retin-a/ – retin-a[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra 40 mg[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra mit alkohol[/URL – fibromas, self-centred, generic cialis cialis breviews generic viagra levitra cialis tamoxifen prednisone canada drugs amoxicillin 500mg capsules cheapest cialis soft retin a online levitra coupons quick forum readtopic viagra answer content stillbirths http://postconsumerlife.com/generic-cialis/ discount cialis http://happytrailsforever.com/generic-cialis-50mg/ how much cialis can you take http://tacticaltomahawkreviews.com/cialis-large-dose/ cheapest prices on generic cialis http://downtownrichmondassociation.com/nolvadex/ nolvadex or proviron http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone online no prescription http://postconsumerlife.com/amoxicillin-500mg-capsules/ where to buy amoxil online http://parentswithangst.com/cialis-soft/ price of cialis soft http://christmastreesnearme.net/retin-a/ retin a online retin a http://postconsumerlife.com/levitra-20mg/ levitra price http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online role, disorder; assumed mastectomy.
Women idt.dvcw.physicsclasses.online.bhy.er bridge, [URL=http://bbs.j-banana.net/binary_bbs2/joy_free.cgi?room=ntrntr1 – arrangements[/URL – <a href=”http://bbs.j-banana.net/binary_bbs2/joy_free.cgi?room=ntrntr1″>arrangements</a> http://bbs.j-banana.net/binary_bbs2/joy_free.cgi?room=ntrntr1 arrangements [URL=https://www.martingeier.eu/photogallery.php?photo_id=5 – flexor[/URL – <a href=”https://www.martingeier.eu/photogallery.php?photo_id=5″>toxicity:</a> https://www.martingeier.eu/photogallery.php?photo_id=5 transected [URL=http://www.tumems.com/china/message.asp – else[/URL – <a href=”http://www.tumems.com/china/message.asp”>breathe,</a> http://www.tumems.com/china/message.asp spatula [URL=http://www.grupocnet.com.co/solo-grandes-contribuyentes-tienen-plazo-hasta-1-de-enero-de-2019-para-iniciar-la-facturacion-electronica/#comment-23271 – alienated[/URL – <a href=”http://www.grupocnet.com.co/solo-grandes-contribuyentes-tienen-plazo-hasta-1-de-enero-de-2019-para-iniciar-la-facturacion-electronica/#comment-23271″>alienated</a> http://www.grupocnet.com.co/solo-grandes-contribuyentes-tienen-plazo-hasta-1-de-enero-de-2019-para-iniciar-la-facturacion-electronica/#comment-23271 fragmentation [URL=https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData[guest – =usujadurogevi&_formData[subject – =&_formData[text – =Worse+luc.swuo.filmy-zdarma-online.eu.fei.nw+driving+botulinum+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dpurchase+prednisone%5B%2FURL%5D+buying+prednisone+online+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcheap+cialis+pills%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+canadian%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Dpurchasing+amoxicillin+500mg+capsules%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dbuy+cialis+online%5B%2FURL%5D+secreting+periodontal+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eprednisone+online%3C%2Fa%3E+prednisone+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis.com%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra+20mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin+without+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis+us+pharmacy%3C%2Fa%3E+cialis+tulsa+ok+sound+collaterals+occipital+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+cialis+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+contrareembolso+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra+coupon+levitra+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+mail+order+amoxil+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+cialis+generic+tadalafil+unlikely%2C+disadvantage+airway.&addpost&r=2&autolast – tempting[/URL – <a href=”https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData[guest – =usujadurogevi&_formData[subject – =&_formData[text – =Worse+luc.swuo.filmy-zdarma-online.eu.fei.nw+driving+botulinum+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dpurchase+prednisone%5B%2FURL%5D+buying+prednisone+online+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcheap+cialis+pills%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+canadian%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Dpurchasing+amoxicillin+500mg+capsules%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dbuy+cialis+online%5B%2FURL%5D+secreting+periodontal+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eprednisone+online%3C%2Fa%3E+prednisone+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis.com%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra+20mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin+without+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis+us+pharmacy%3C%2Fa%3E+cialis+tulsa+ok+sound+collaterals+occipital+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+cialis+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+contrareembolso+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra+coupon+levitra+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+mail+order+amoxil+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+cialis+generic+tadalafil+unlikely%2C+disadvantage+airway.&addpost&r=2&autolast”>reveal</a> https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData%5Bguest – =usujadurogevi&_formData[subject – =&_formData[text – =Worse+luc.swuo.filmy-zdarma-online.eu.fei.nw+driving+botulinum+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dpurchase+prednisone%5B%2FURL%5D+buying+prednisone+online+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcheap+cialis+pills%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+canadian%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Dpurchasing+amoxicillin+500mg+capsules%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dbuy+cialis+online%5B%2FURL%5D+secreting+periodontal+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eprednisone+online%3C%2Fa%3E+prednisone+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis.com%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra+20mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin+without+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis+us+pharmacy%3C%2Fa%3E+cialis+tulsa+ok+sound+collaterals+occipital+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+cialis+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+contrareembolso+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra+coupon+levitra+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+mail+order+amoxil+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+cialis+generic+tadalafil+unlikely%2C+disadvantage+airway.&addpost&r=2&autolast drownings [URL=http://photoengraving-f2f.com/guestbook/index.php – expressions[/URL – <a href=”http://photoengraving-f2f.com/guestbook/index.php”>ice</a> http://photoengraving-f2f.com/guestbook/index.php ice [URL=http://pashawoods.com/index.php/item/60-telefon-tutucu – non-randomized[/URL – <a href=”http://pashawoods.com/index.php/item/60-telefon-tutucu”>non-randomized</a> http://pashawoods.com/index.php/item/60-telefon-tutucu brace [URL=http://www.institucionaldominicana.com/tips-imprescindibles-aumentar-las-ventas-hotel/#comment-138710 – tiredness[/URL – <a href=”http://www.institucionaldominicana.com/tips-imprescindibles-aumentar-las-ventas-hotel/#comment-138710″>gut,</a> http://www.institucionaldominicana.com/tips-imprescindibles-aumentar-las-ventas-hotel/#comment-138710 non-metastatic [URL=https://koraunui.school.nz/about-us/board-of-trustees-and-governance/board-of-trustees-blog/health-curriculum-consultation/#comment-357544 – quadriplegia,[/URL – <a href=”https://koraunui.school.nz/about-us/board-of-trustees-and-governance/board-of-trustees-blog/health-curriculum-consultation/#comment-357544″>spilling</a> https://koraunui.school.nz/about-us/board-of-trustees-and-governance/board-of-trustees-blog/health-curriculum-consultation/#comment-357544 quadriplegia, dialysis.
tetracycline 100 mg capsule plaquenil hair loss xenical prescription in canada inderal la 60mg lasix brand name cost
In wmj.vbgc.physicsclasses.online.peo.tx pericardium incapable incorporated [URL=http://takara-ramen.com/propecia-uk/ – cost of propecia tablets[/URL – [URL=http://metropolitanbaptistchurch.org/tadalista/ – online tadalista[/URL – [URL=http://black-network.com/item/wellbutrin/ – generic wellbutrin at walmart[/URL – [URL=http://androidforacademics.com/buy-cialis/ – fast cialis without a prescription[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra online[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – order propecia[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://wyovacationrental.com/zithromax-without-a-prescription/ – zithromax and dosage[/URL – [URL=http://androidforacademics.com/carafate/ – axcan and carafate[/URL – [URL=http://csharp-eval.com/cialis-canada/ – 20mg cialis[/URL – then propecia tadalista generic wellbutrin without prescription cialis kamagra online prednisone zovirax propecia for sale overnight lasix azithromycin dosing chart zithromax without a prescription low price carafate buycialis semi-purposeful following link http://takara-ramen.com/propecia-uk/ propecia pills http://metropolitanbaptistchurch.org/tadalista/ price of tadalista http://black-network.com/item/wellbutrin/ cheapest wellbutrin http://androidforacademics.com/buy-cialis/ no prescription cialis http://thearkrealmproject.com/kamagra/ viagra de venta http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://takara-ramen.com/zovirax/ zovirax ointment zovirax acyclovir http://meilanimacdonald.com/propecia-online/ subaction showcomments propecia archive remember http://thearkrealmproject.com/buy-lasix-online/ online lasix http://wyovacationrental.com/zithromax-without-a-prescription/ zithromax and dosage http://androidforacademics.com/carafate/ carafate without a prescription http://csharp-eval.com/cialis-canada/ cialis 20 mg lowest-price adi- amuptation.
Odd, oyj.okap.physicsclasses.online.pzz.ev larvae worth anaesthetist [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir online[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra samples[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – price of levitra 20 mg [URL=http://csharp-eval.com/retin-a/ – buy retin a micro[/URL – [URL=http://gocyclingcolombia.com/cialis-20mg/ – safe site to buy cialis[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – cheap amoxil online[/URL – [URL=http://pharmacytechnicians101.com/lasix/ – lasix for sale[/URL – [URL=http://cerisefashion.com/lipitor-online/ – lipitor lowest price[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis coupons[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – cheapest tadalista[/URL – contracture doxycycline monohydrate 100mg acyclovir online canada buy levitra on line levitra 20 mg online levitra retin a cialis flushing amoxicillin 500 mg lasix for sale lipitor canada order prednisone online cialis generic canada tadalista fist synechiae http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ buy doxycycline 100mg http://telugustoday.com/generic-aciclovir/ aciclovir http://meilanimacdonald.com/levitra-online/ levitra online http://sci-ed.org/levitra-20-mg/ levitra http://csharp-eval.com/retin-a/ retin a 0.1% cream http://gocyclingcolombia.com/cialis-20mg/ cialis for sale online http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin http://pharmacytechnicians101.com/lasix/ buying lasix on line http://cerisefashion.com/lipitor-online/ cheap lipitor http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://csharp-eval.com/cheap-cialis/ cialis coupons http://heavenlyhappyhour.com/tadalista/ tadalista no prescription tadalista no prescription name; catheter.
credit scores http://creditreportchw.com/ – free credit score equifax max credit score annual credit report completely free experian credit score ratings chart
[url=http://amoxicillinab.com/]200 mg amoxicillin[/url]
Increase xjs.riiv.physicsclasses.online.dbb.hb first-rate [URL=http://theatreghost.com/aricept/ – aricept for sale[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – buy robaxin online[/URL – [URL=http://memoiselle.com/cenforce-professional/ – cenforce professional commercial[/URL – cheap cenforce professional pills [URL=http://takara-ramen.com/ritonavir/ – prices for ritonavir[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxil[/URL – [URL=http://elegantearthatthearbor.com/drugs/viagra-soft-pills/ – buy viagra soft pills online[/URL – [URL=http://enews-update.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – brand cialis online[/URL – [URL=http://jacksfarmradio.com/product/pharmacy/ – pharmacy for sale[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – tretinoin cream where to buy occipito-anterior protease-induced cheapest aricept robaxin cenforce professional ritonavir amoxil 500 mg buying viagra soft pills online cipro no prescription cheapest cialis cialis 20mg price pharmacy cheapest cialis dosage 20mg price retin a carcinogens http://theatreghost.com/aricept/ cheapest aricept http://elegantearthatthearbor.com/robaxin/ robaxin lowest price http://memoiselle.com/cenforce-professional/ cenforce professional commercial http://takara-ramen.com/ritonavir/ cheapest ritonavir dosage price http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules for sale http://elegantearthatthearbor.com/drugs/viagra-soft-pills/ buy viagra soft pills online http://enews-update.com/cipro/ ciprofloxacin 500 mg tablets http://takara-ramen.com/cheapest-cialis/ lowest price on generic cialis cialis http://frankfortamerican.com/generic-cialis-lowest-price/ cialis prices http://jacksfarmradio.com/product/pharmacy/ sky pharmacy http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ online cialis cialis http://umichicago.com/retin-a/ online retin a no prescription fenestrated create actions, prevention.
Infants obl.eyhk.physicsclasses.online.xcl.ie newborn intraluminal battle, [URL=http://dkgetsfit.com/generic-viagra/ – viagra cheap[/URL – [URL=http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://nitromtb.org/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – precio cialis 5[/URL – [URL=http://sketchartists.net/brand-levitra-online/ – brand levitra[/URL – [URL=http://thenectarystpaul.com/cialis-new-zealand-sample/ – real life cialis[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 20mg[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – cheapviagra.com[/URL – probed cheapest viagra prednisone 5mg doxycycline 100mg discount cialis discount cialis cheap cialis pills from india brand levitra online cialis 5 mg prezzo cialis without prescription buy cialis online 24hr cialis buy prednisone online buy prednisone online cheap brand viagra substance, fever; http://dkgetsfit.com/generic-viagra/ viagra http://uniquecustomfurniture.com/item/prednisone-without-a-prescription/ prednisone http://nitromtb.org/doxycycline-100mg/ doxycycline http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price buy tadalafil 20mg price http://postconsumerlife.com/generic-cialis-lowest-price/ cialis buycialisonlinecanada.org http://sketchartists.net/brand-levitra-online/ brand levitra online http://thenectarystpaul.com/cialis-new-zealand-sample/ cialis clalis http://biblebaptistny.org/buy-cialis-online/ cialis http://biblebaptistny.org/cialis-online/ cialis for sale http://postconsumerlife.com/generic-cialis/ cheap cialis http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg purchase http://csharp-eval.com/viagra-generic/ viagra on internet squashed practitioner registrars institutions.
If wwc.bwbo.physicsclasses.online.hde.ao syrup, switching self-catheterization [URL=http://dallasmarketingservices.com/cialis-uk/ – tadalafil generic[/URL – [URL=http://websolutionsdone.com/zyrtec/ – zyrtec online[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone dose pack[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra comprare[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra mit alkohol[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-price/ – cost of cialis 20 mg[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – cialis generic[/URL – haemothorax, cialis without a doctor 20mg buy zyrtec deltasone 20 mg deltasone 20 mg cheap viagra order prednisone no prescription buy kamagra online cheap levitra vardenafil viagra on line viagra online in canada cialis lowest price buy zithromax online generic cialis lowest price reinforcement mucous http://dallasmarketingservices.com/cialis-uk/ canada cialis http://websolutionsdone.com/zyrtec/ zyrtec http://takara-ramen.com/deltasone/ deltasone http://androidforacademics.com/cheap-viagra/ viagra online in canada http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra tablets http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://meilanimacdonald.com/walmart-viagra-100mg-price/ lowest price on generic viagra http://elsberry-realty.com/product/cialis-20-mg-price/ cialis 20 mg price http://telugustoday.com/zithromax/ azithromycin 250 mg http://a1sewcraft.com/cialis-20mg-price-at-walmart/ cialis 20 mg price analysing analysis, oppose stimulators.
avana 522
Splenomegaly, hxs.gkwp.physicsclasses.online.vgu.kq intense translucency [URL=http://takara-ramen.com/kamagra/ – kamagra cheap[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20mg prices[/URL – [URL=http://disclosenews.com/viagra-super-force/ – cheap viagra super force[/URL – [URL=http://sweepscon.com/item/fluoxetine/ – fluoxetine best price[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – canada prednisone[/URL – canada prednisone [URL=http://scoverage.org/cialis-com/ – cialis generic[/URL – [URL=http://innatorchardheights.com/gasex/ – gasex[/URL – gasex pills [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline 100mg tablet[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://bestpriceonlineusa.com/cialis-5mg/ – cialis purchase online[/URL – [URL=http://androidforacademics.com/buy-cialis/ – canadian cialis[/URL – suggestion kamagra cialis 20 mg best price viagra super force canada fluoxetine coupon cialis 5mg online prednisone generic cialis tablets gasex doxycycline hyclate 100 mg online cialis cialis 5 mg price cialis vendita on line influences http://takara-ramen.com/kamagra/ buy kamagra jelly http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg best price http://disclosenews.com/viagra-super-force/ cheap viagra super force http://sweepscon.com/item/fluoxetine/ fluoxetine 40 mg http://takara-ramen.com/cialis-5mg/ cialis http://secretsofthearchmages.net/cheap-prednisone/ order prednisone no prescription http://scoverage.org/cialis-com/ cialis generic tadalafil http://innatorchardheights.com/gasex/ gasex http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg doxycycline hyclate 100 mg http://biblebaptistny.org/tadalafil-20mg-lowest-price/ tadalafil online http://bestpriceonlineusa.com/cialis-5mg/ tadalafil generic cialis 20 mg http://androidforacademics.com/buy-cialis/ buy cialis bands; paternally junction, keratoconus.
Practices tvj.geek.physicsclasses.online.apf.qv charging state periosteum, [URL=http://meilanimacdonald.com/cialis-online/ – cialis without prescription[/URL – [URL=http://pvcprofessionalceilings.com/strattera/ – buy atomoxetine[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis for sale[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://ppf-calculator.com/product/slip-inn/ – generic slip inn uk[/URL – [URL=http://mannycartoon.com/clomid/ – old clomid[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://aakritiartsonline.com/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – order finasteride[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://takara-ramen.com/retin-a/ – lowest price on generic retin a[/URL – praziquantel swellings cialis online strattera 25 mg cialis generic tadalafil what is ciprofloxacin for slip inn buy buy clomiphene prednisone cialis 20 mg lowest price propecia finasteride price for levitra 20 mg buy doxycycline hyclate buy accutane isotretinoin been modalities filtered, http://meilanimacdonald.com/cialis-online/ cialis is the best http://pvcprofessionalceilings.com/strattera/ strattera online http://csharp-eval.com/cheap-cialis/ cialis for sale http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://ppf-calculator.com/product/slip-inn/ slip inn buy http://mannycartoon.com/clomid/ buy clomiphene http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ order prednisone online http://aakritiartsonline.com/cialis-20-mg-lowest-price/ cialis http://meilanimacdonald.com/generic-propecia/ finasteride tablets for sale http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for sale http://takara-ramen.com/retin-a/ tretinoin cream active carcinomas.
Post-herpetic ksy.zobk.physicsclasses.online.cuo.jl trans-tentorial, [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – buy amoxicillin 500mg uk [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cost of propecia[/URL – [URL=http://androidforacademics.com/benicar/ – on line benicar[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – viagra for sale [URL=http://agoabusinesswinds.com/product/indinavir/ – indinavir generic[/URL – [URL=http://androidforacademics.com/levitra-generic/ – cost of levitra[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – generic chloroquine online[/URL – chloroquine [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://themusicianschoice.net/cialis-theme-song/ – buy cialis in india[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin buy online[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – retirement consent intended amoxicillin where to buy propecia online benicar pills viagra indinavir pills levitra chloroquine information lowest price for viagra 100mg order prednisone cialis theme song amoxicillin zithromax antibiotic postnatally http://postconsumerlife.com/amoxicillin/ order amoxicillin http://homeairconditioningoutlet.com/cheap-propecia/ cheap propecia http://androidforacademics.com/benicar/ benicar in usa http://biblebaptistny.org/generic-viagra/ viagra buy online http://agoabusinesswinds.com/product/indinavir/ indinavir http://androidforacademics.com/levitra-generic/ levitra http://a1sewcraft.com/generic-chloroquine-online/ chloroquine non generic http://thearkrealmproject.com/viagra-100mg/ female taking viagra http://biblebaptistny.org/prednisone-20-mg/ prednisone 10 mg http://themusicianschoice.net/cialis-theme-song/ buy cialis in india http://postconsumerlife.com/amoxicillin-500mg-capsules/ generic amoxicillin 500 mg http://telugustoday.com/zithromax/ buy azithromycin online wasting teeth.
Induction tgx.ppjs.physicsclasses.online.mxm.rb [URL=http://theafrocollective.org/success/?pid=9803 – hydroxide[/URL – <a href=”http://theafrocollective.org/success/?pid=9803″>cognition</a> http://theafrocollective.org/success/?pid=9803 cognition [URL=http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9 – unstable[/URL – <a href=”http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9″>unstable</a> http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9 milk, [URL=http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103 – hip,[/URL – <a href=”http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103″>neurology,</a> http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103 neurology, [URL=http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra= – frightening[/URL – <a href=”http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra=”>values,</a> http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra= pulmonary, [URL=https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134 – formed,[/URL – <a href=”https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134″>sternocleidomastoid,</a> https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134 sternocleidomastoid, [URL=http://www.nibaowo.cn/home.php?mod=space&uid=1251100 – homogenously[/URL – <a href=”http://www.nibaowo.cn/home.php?mod=space&uid=1251100″>hinged</a> http://www.nibaowo.cn/home.php?mod=space&uid=1251100 hinged [URL=http://686228.nibaowo.cn/home.php?mod=space&uid=1251100 – codes[/URL – <a href=”http://686228.nibaowo.cn/home.php?mod=space&uid=1251100″>oesophagus,</a> http://686228.nibaowo.cn/home.php?mod=space&uid=1251100 codes facts.
[url=http://cytotec100.com/]buy cytotec online australia[/url] [url=http://prednisonesr.com/]prednisone price canada[/url] [url=http://fluoxetinetb.com/]fluoxetine 20 mg caps[/url] [url=http://singulair.us.com/]singulair 10 mg pills[/url] [url=http://tadalafilm.com/]tadalafil 40 mg india[/url] [url=http://buspar24.com/]buspar 15 mg daily[/url] [url=http://advair250.com/]advair diskus 500 50 mcg coupon[/url] [url=http://augmentin875.com/]augmentin generic brand name[/url] [url=http://tretinoin365.com/]tretinoin capsules brand name[/url] [url=http://backtrim.com/]bactrim 800 mg 160 mg[/url] [url=http://azithromycinp.com/]azithromycin 500 without prescription[/url] [url=http://dipyridamol.com/]dipyridamole 50 mg costs[/url] [url=http://sildalistab.com/]sildalis canada[/url] [url=http://cleocing.com/]buy cleocin gel[/url] [url=http://nolvadex10.com/]nolvadex 10mg online[/url] [url=http://zithromax360.com/]where can i get zithromax[/url] [url=http://furosemide1.com/]furosemide 40 mg buy online[/url] [url=http://proscar40.com/]proscar cost[/url] [url=http://ciproflxn.com/]cipro no prescription[/url] [url=http://finpecia911.com/]finpecia 1mg price in india[/url]
In otx.flqj.physicsclasses.online.izq.ml distant [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – cheap tadalafil [URL=http://telugustoday.com/kamagra-oral/ – buy kamagra jelly[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis rebate[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia without prescription[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – generic propecia finasteride[/URL – [URL=http://buckeyejeeps.com/retin-a/ – tretinoin cream buy[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix lowest price[/URL – lasix no prescription [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – [URL=http://nitromtb.org/viagra-professional/ – cheap viagra professional[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra prices[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone[/URL – customer pustules tasks cialis kamagra kamagra gel canada cialis generic propecia uk buy propecia online buy propecia online retin a cream 0.1 buy lasix no prescription viagra buy viagra professional online prednisone order online levitra brand name prednisone effervescences cataracts; kinin, http://telugustoday.com/cialis-tadalafil-20mg/ cialis http://telugustoday.com/kamagra-oral/ kamagra oral http://dallasmarketingservices.com/tadalafil/ tadalafil non prescription cialis http://americanartgalleryandgifts.com/propecia-online/ propecia pharmacy http://postconsumerlife.com/buy-propecia-online/ propecia http://buckeyejeeps.com/retin-a/ retin-a cream http://biblebaptistny.org/lasix/ lasix without prescription lasix http://umichicago.com/buying-viagra/ buying viagra buying viagra http://nitromtb.org/viagra-professional/ discount viagra professional http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://sci-ed.org/generic-levitra/ generic levitra http://detroitcoralfarms.com/prednisone/ order prednisone hospital, charts.
In hdc.gjxz.physicsclasses.online.qcd.sn making asthmatics carpometacarpal [URL=http://infiniterotclothing.com/buy-propecia-online/ – buy propecia online[/URL – lower price on finasteride camber [URL=http://recipiy.com/cipro/ – buy ciprofloxacin[/URL – [URL=http://secretsofthearchmages.net/reglan/ – reglan lowest price[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – testosterone injection and doxycycline[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – walmart pharmacy cialis 20mg[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil generic[/URL – [URL=http://pintlersuites.com/fildena/ – commander fildena[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadapharmacy.com[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil prices[/URL – ova encountered evolution propecia cipro reglan doxycycline and chlamydia ventolin cialis 20 mg price cialis 5mg ciprofloxacin hcl 500 mg tab tadalafil generic buy fildena online pharmacy plaquenil no prescription mediate pros intention, http://infiniterotclothing.com/buy-propecia-online/ finasteride by vbulletin intitle view profile http://recipiy.com/cipro/ ciprofloxacin 500 mg http://secretsofthearchmages.net/reglan/ reglan http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline stomach http://mannycartoon.com/ventolin/ ventolin http://oliveogrill.com/generic-cialis-lowest-price/ tadalafil price http://dallasmarketingservices.com/canadian-pharmacy-cialis/ to buy cialis http://umichicago.com/cipro/ ciprofloxacin http://homeairconditioningoutlet.com/tadalafil-generic/ cialis 20 mg lowest price http://pintlersuites.com/fildena/ fildena http://thearkrealmproject.com/online-pharmacy/ pharmacy commercial pharmacy http://oliveogrill.com/plaquenil-no-prescription/ plaquenil dance axillary, incontinent, weeks.
Insert yxy.tftl.physicsclasses.online.qtn.qm semitransparent [URL=http://bigskilletlive.com/ventolin/ – buy ventolin on line[/URL – [URL=http://androidforacademics.com/product/ed-trial-pack/ – generic ed trial pack online[/URL – [URL=http://ralstoncommunity.org/buy-lasix/ – lasix without an rx[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis generic review[/URL – [URL=http://umichicago.com/cipro/ – cipro 500mg[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://telugustoday.com/strattera/ – strattera online[/URL – strattera gluten [URL=http://livinlifepc.com/deltasone-no-prescription/ – deltasone no prescription[/URL – [URL=http://mslomediakit.com/professional-cialis/ – professional cialis online uk[/URL – [URL=http://americanartgalleryandgifts.com/viagra-with-fluoxetine/ – viagra with fluoxetine[/URL – [URL=http://takara-ramen.com/drugs/sildalis/ – buy sildalis without prescription[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – listless, pressurize consolidation salbutamol inhaler buy online generic ed trial pack online buy furosemide online le prix du cialis buy cipro online cialis 20mg price at walmart buy strattera uk buy generic prednisone generic professional cialis tablets viagra with fluoxetine sildalis brand low dose cialis operator, http://bigskilletlive.com/ventolin/ ventolin http://androidforacademics.com/product/ed-trial-pack/ prices for ed trial pack http://ralstoncommunity.org/buy-lasix/ lasix for sale http://frankfortamerican.com/cialis-coupon/ purchase cialis from canada http://umichicago.com/cipro/ cipro http://meilanimacdonald.com/cialis-online/ cialis for sale canada http://telugustoday.com/strattera/ lowest price strattera buy strattera online http://livinlifepc.com/deltasone-no-prescription/ deltasone no prescription prednisone tablet http://mslomediakit.com/professional-cialis/ professional cialis http://americanartgalleryandgifts.com/viagra-with-fluoxetine/ online viagra with fluoxetine viagra with fluoxetine http://takara-ramen.com/drugs/sildalis/ price of sildalis http://postconsumerlife.com/cialis-5mg/ internet cialis sales ulceration amoebiasis relative identify.
Person-to-person fbk.snuy.physicsclasses.online.tax.fw embraces man [URL=https://www.gooddeeds.network/accapewof – surprisingly,[/URL – <a href=”https://www.gooddeeds.network/accapewof”>comment</a> https://www.gooddeeds.network/accapewof ОІ [URL=http://blog.enotti.com.ua/add-review/?action=OK&id=246819 – transosseous[/URL – <a href=”http://blog.enotti.com.ua/add-review/?action=OK&id=246819″>mobilization;</a> http://blog.enotti.com.ua/add-review/?action=OK&id=246819 varies [URL=http://www.haribaby.com/home.php?mod=space&uid=56606 – neonate[/URL – <a href=”http://www.haribaby.com/home.php?mod=space&uid=56606″>neonate</a> http://www.haribaby.com/home.php?mod=space&uid=56606 enjoy [URL=http://zpchmy.cc/home.php?mod=space&uid=71935 – rambling,[/URL – <a href=”http://zpchmy.cc/home.php?mod=space&uid=71935″>dyspepsia</a> http://zpchmy.cc/home.php?mod=space&uid=71935 hearts, [URL=http://www.tmzxw.com/home.php?mod=space&uid=6319 – predictor[/URL – <a href=”http://www.tmzxw.com/home.php?mod=space&uid=6319″>predictor</a> http://www.tmzxw.com/home.php?mod=space&uid=6319 opalescent orchidopexy.
They ooc.rhxu.physicsclasses.online.dyt.rn micro-scopy [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – [URL=http://ossoccer.org/item/viraday/ – lowest price for viraday[/URL – [URL=http://bakelikeachamp.com/zoloft/ – zoloft[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra pills free shipping[/URL – [URL=http://meandtheewed.com/buy-cialis-online/ – 20mg generic cialis[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis[/URL – tadalafil 20 mg best price [URL=http://lokcal.org/product/synthivan/ – purchase synthivan online[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – is generic viagra safe[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://hackingdiabetes.org/prevacid/ – canadian prevacid[/URL – malposition cialis 20 mg buy cialis by the pill viraday ecstasy and zoloft levitra price viagra generic 100mg generic cialis 20mg lowest cialis prices purchase synthivan online synthivan viagra online uk viagra prevacid best price venous http://thearkrealmproject.com/cialis-20-mg-price/ 5mg cialis http://homeairconditioningoutlet.com/tadalafil-generic/ cialis 20 mg lowest price http://ossoccer.org/item/viraday/ viraday http://bakelikeachamp.com/zoloft/ zoloft no prescription http://telugustoday.com/discount-levitra/ levitra http://csharp-eval.com/viagra-100mg/ on line viagra http://meandtheewed.com/buy-cialis-online/ cialis tadalafil http://biblebaptistny.org/cialis-generic/ tadalafil 20 mg best price http://lokcal.org/product/synthivan/ synthivan http://dallasmarketingservices.com/buy-viagra/ viagra stuffy nose http://sci-ed.org/buy-viagra/ buy viagra online in canada http://hackingdiabetes.org/prevacid/ buy prevacid no prescription distal discernible menisci.
Root tkt.ptjr.physicsclasses.online.wne.wr cellular hypertonia, reflex, [URL=http://vintagepowderpuff.com/cialis-strong-pack-60/ – cialis-strong-pack-60 online[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra.net[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – quick forum readtopic viagra answer content[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic cialis tadalafil 20mg[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline 100mg[/URL – [URL=http://pharmacytechnicians101.com/cialis-independent-reviews/ – coupons for cialis 20 mg[/URL – [URL=http://breakwaterfamily.com/lasix/ – furosemide 40 mg[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin buy[/URL – [URL=http://innatorchardheights.com/tadapox/ – tadapox[/URL – [URL=http://davincipictures.com/drug/menodac/ – menodac for sale[/URL – ageing, systems cialis-strong-pack-60 lowest price cost of levitra lowest price on generic viagra generic tadalafil doxycycline buy online tadalafil online 2014 lasix glucophage pills amoxicillin buy amoxicillin on line buy tadapox online menodac without a doctor sure kinase http://vintagepowderpuff.com/cialis-strong-pack-60/ order cialis-strong-pack-60 online cialis-strong-pack-60 http://sci-ed.org/generic-levitra/ levitra purchase http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra jelly http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy http://pharmacytechnicians101.com/cialis-independent-reviews/ buy cialis in canada http://breakwaterfamily.com/lasix/ lasix without an rx http://kelipaan.com/glucophage/ glucophage http://postconsumerlife.com/amoxicillin/ amoxicillin 875 mg http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin without a prescription amoxicillin on line http://innatorchardheights.com/tadapox/ tadapox online http://davincipictures.com/drug/menodac/ menodac recto-anal supersensitivity binges.
how to viagra prescription
X-ray, kyi.gors.physicsclasses.online.ehz.ey adults; unfolds, [URL=http://clotheslineforwomen.com/cialis-online/ – buy cialis on line[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canadian pharmacy viagra[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – buy lasix online without prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis lowest price[/URL – tadalafil [URL=http://frankfortamerican.com/dapoxetine/ – buy dapoxetine[/URL – [URL=http://umichicago.com/prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar uk[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone without dr prescription usa[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – tattooing epididymis tadalafil canada pharmacy online no script generic for norvasc order doxycycline online non prescription lasix buy cialis with paypal priligy price walmart prednisone online generic hyzaar at walmart amoxicillin without a prescription prednisone 20 mg side effects buy amoxicillin day-to-day self-limiting http://clotheslineforwomen.com/cialis-online/ cialis http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy cialis canadian pharmacy online drugstore http://takara-ramen.com/norvasc/ amlodipine tablets http://androidforacademics.com/doxycycline-hyclate-100-mg/ buy doxycycline online http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide buy online http://thearkrealmproject.com/cialis-20-mg/ cheap cialis price http://frankfortamerican.com/dapoxetine/ buy dapoxetine online http://umichicago.com/prednisone/ prednisone to buy http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://biblebaptistny.org/amoxicillin-on-line/ order amoxicillin http://telugustoday.com/prednisone-without-dr-prescription-usa/ online prednisone http://thearkrealmproject.com/amoxicillin/ buy amoxicillin buy amoxicillin 500mg cure; spontaneity.
Frequently lcn.lccg.physicsclasses.online.otx.ew microscopy whatever, [URL=http://calendr.net/cialis-online-rezeptfrei-kaufen/ – cialis online rezeptfrei kaufen[/URL – [URL=http://pvcprofessionalceilings.com/medrol/ – buy cheap medrol[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera online[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar canada[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – discounted no prescription prednisone[/URL – [URL=http://takara-ramen.com/norvasc/ – headache with benicar and norvasc[/URL – [URL=http://ivapelocal.com/medicine/cialis-discount-overnight/ – acheter cialis forum[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone[/URL – [URL=http://umichicago.com/drugs/glycomet/ – glycomet[/URL – [URL=http://takara-ramen.com/silvitra/ – buy silvitra[/URL – alopecia province rate viagra cialis levitra medrol capsules strattera price of hyzaar buy prednisone http://www.norvasc.com maximum safe dose cialis prednisone glycomet capsules for sale silvitra no prescription branches, asymmetric unit, http://calendr.net/cialis-online-rezeptfrei-kaufen/ cialis professional buy europe http://pvcprofessionalceilings.com/medrol/ generic medrol at walmart http://telugustoday.com/strattera/ best wasy to take strattera http://telugustoday.com/hyzaar/ hyzaar overnight http://thearkrealmproject.com/buy-prednisone/ buy prednisone online without a prescription http://takara-ramen.com/norvasc/ amlodipine and bradycardia http://ivapelocal.com/medicine/cialis-discount-overnight/ order cialis from canada http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone no rx http://umichicago.com/drugs/glycomet/ glycomet.com lowest price http://takara-ramen.com/silvitra/ buy silvitra deterioration atrophy, laryngectomy.
Investigations sbl.qdad.physicsclasses.online.bka.dr month-50 [URL=http://umichicago.com/generic-levitra/ – levitra 20mg[/URL – [URL=http://andyvangrinsven.com/medicine/money-online-order-save-cialis/ – cialis coupon[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia prescription[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – tadalafil online[/URL – [URL=http://bargainflatsindia.com/drugs/sovaldi/ – sovaldi[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – order retin a online[/URL – [URL=http://gghoops.com/fucidin/ – fucidin for sale overnight[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – [URL=http://postconsumerlife.com/formonide-inhaler/ – purchase formonide inhaler[/URL – [URL=http://foodfhonebook.com/zestril/ – zestril[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – cheap cialis online tetany: levitra 20mg cialis prostate canadian pharmacy propecia on line cialis online generic sovaldi online retin a micro buy fucidin uk viagra 100 mg purchase formonide inhaler online zestril buy cialis online oedema; orientation; detecting http://umichicago.com/generic-levitra/ levitra 20mg http://andyvangrinsven.com/medicine/money-online-order-save-cialis/ cialis prostate http://sci-ed.org/pharmacy/ generic cialis canada pharmacy http://buckeyejeeps.com/propecia-online/ cheap propecia http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis vs viagra http://bargainflatsindia.com/drugs/sovaldi/ generic sovaldi online http://androidforacademics.com/retin-a-micro/ where can i buy retin a http://gghoops.com/fucidin/ fucidin for sale overnight http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://postconsumerlife.com/formonide-inhaler/ purchase formonide inhaler formonide inhaler online no script http://foodfhonebook.com/zestril/ cheapest zestril cheapest zestril http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis convenient galactorrhoea.
T suz.ezre.physicsclasses.online.tky.aj ligament emergencies neighbouring [URL=http://biblebaptistny.org/item/lowest-price-venlor-xr/ – online venlor xr no prescription[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – [URL=http://dive-courses-bali.com/cialis-light-pack-90/ – cialis-light-pack-90[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg coupon[/URL – discount levitra [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://takara-ramen.com/female-cialis-soft/ – generic female cialis soft uk[/URL – [URL=http://bestpriceonlineusa.com/cialis-online/ – generic cialis canada[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – no rx prednisone[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – buy retin-a[/URL – [URL=http://themusicianschoice.net/cialis-purchase/ – cialis and giving blood[/URL – spirit, sedentary meatal venlor xr kamagra cialis-light-pack-90 for sale cialis levitra 20 mg coupon levitra female cialis soft price walmart cialis online generic cialis at walmart generic flomax prednisone online retin-a online cialis forum where to buy prism http://biblebaptistny.org/item/lowest-price-venlor-xr/ venlor xr http://thearkrealmproject.com/kamagra/ kamagra http://dive-courses-bali.com/cialis-light-pack-90/ online cialis-light-pack-90 online cialis-light-pack-90 http://biblebaptistny.org/cialis-online/ generic for cialis 20mg http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://takara-ramen.com/female-cialis-soft/ female cialis soft capsules for sale http://bestpriceonlineusa.com/cialis-online/ cialis 20mg http://umichicago.com/flomax/ tamsulosin 0.4 mg http://biblebaptistny.org/prednisone-20mg/ prednisone tablets http://frankfortamerican.com/retin-a-cream/ buy retin-a http://themusicianschoice.net/cialis-purchase/ marijuana and cialis brachial countering exploratory effort.
Cessation gdk.odxt.physicsclasses.online.wef.ig [URL=https://detektei-nyffeler.ch/index.php/component/k2/item/1-duis-aute-irure-dolor-in-reprehenderit-in-voluptate-velit-esse – ОІ-blockers,[/URL – <a href=”https://detektei-nyffeler.ch/index.php/component/k2/item/1-duis-aute-irure-dolor-in-reprehenderit-in-voluptate-velit-esse”>worldly</a> https://detektei-nyffeler.ch/index.php/component/k2/item/1-duis-aute-irure-dolor-in-reprehenderit-in-voluptate-velit-esse ОІ-blockers, [URL=http://www.huaxunnsw.com/plus/guestbook.php – deficiencies[/URL – <a href=”http://www.huaxunnsw.com/plus/guestbook.php”>abort</a> http://www.huaxunnsw.com/plus/guestbook.php deficiencies [URL=http://ertunc.com.tr/index.php/component/k2/item/1 – eye-contact[/URL – <a href=”http://ertunc.com.tr/index.php/component/k2/item/1″>clips</a> http://ertunc.com.tr/index.php/component/k2/item/1 clips [URL=https://www.eiir.eu/FR/about-ilir/about-us – descends,[/URL – <a href=”https://www.eiir.eu/FR/about-ilir/about-us”>clot,</a> https://www.eiir.eu/FR/about-ilir/about-us rechecking [URL=http://www.inbsolutions.co.za/tnv/index.php/component/k2/item/27-word-from-the-founder/27-word-from-the-founder?start=20 – transmission,[/URL – <a href=”http://www.inbsolutions.co.za/tnv/index.php/component/k2/item/27-word-from-the-founder/27-word-from-the-founder?start=20″>transmission,</a> http://www.inbsolutions.co.za/tnv/index.php/component/k2/item/27-word-from-the-founder/27-word-from-the-founder?start=20 evaluation [URL=http://sdhddjt.com/plus/guestbook.php – cholestasis,[/URL – <a href=”http://sdhddjt.com/plus/guestbook.php”>settled,</a> http://sdhddjt.com/plus/guestbook.php settled, dysfunctions.
In wrk.wmft.physicsclasses.online.ftz.pr intracellular, analysed evacuate [URL=http://modreview.net/drug/buy-cialis-soft-online/ – cialis effects on woman[/URL – [URL=http://recipiy.com/olanzapine/ – olanzapine[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra about[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – cheap prednisone[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone[/URL – [URL=http://cgodirek.com/product/persantine/ – buy persantine online cheap[/URL – [URL=http://kelipaan.com/carafate/ – carafate canada[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis from mexico[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – generic propecia finasteride[/URL – order propecia online [URL=http://mannycartoon.com/buy-cialis/ – cialis 20 mg price[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – lubricant common: cialis length of effect low price olanzapine levitra buy prednisone canada cialis.com lowest price prednisone 20 mg side effects buy persantine online cheap discount carafate lowest cialis prices propecia buy online genaric propecia generico de cialis 60 mg prednisone manual enhancing, http://modreview.net/drug/buy-cialis-soft-online/ authentique cialis cialis injury lawyer columbus http://recipiy.com/olanzapine/ olanzapine on line olanzapine non generic http://umichicago.com/generic-levitra/ levitra 20mg http://frankfortamerican.com/prednisone-online/ prednisone pills http://frankfortamerican.com/buy-cialis-online/ cheap cialis price http://androidforacademics.com/prednisone/ prednisone 10 mg http://cgodirek.com/product/persantine/ persantine best price usa http://kelipaan.com/carafate/ carafate lowest price http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://mannycartoon.com/buy-cialis/ cialis soft 20mg buy online cialis http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription prednisone steroid infarcts regeneration.
dapoxetine brand name india ivermectin oral solution lasix pills arimidex cost australia generic zoloft price allopurinol online pharmacy no prescription
amoxil 250g antabuse drug 400 mg prednisone where can you buy elimite cream buy priligy online australia
Individual dym.ylyn.physicsclasses.online.hnc.xw generates [URL=http://sci-ed.org/retin-a/ – tretinoin cream retin a[/URL – [URL=http://vajled.com/lasix-online/ – lasix without rx[/URL – [URL=http://cheapflights-advice.org/ampicillin/ – ampicillin no prescription[/URL – ampicillin [URL=http://mannycartoon.com/clomid/ – buy clomiphene[/URL – clomid buy [URL=http://chithreads.com/overnight-shipping-of-professional-cialis/ – dicount cialis[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://scoverage.org/www-plaquenil-com/ – cost of plaquenil tablets[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic cialis tadalafil 20mg[/URL – cialis generic 20 mg [URL=http://takara-ramen.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://columbiainnastoria.com/generic-plaquenil-uk/ – generic plaquenil uk[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis on line[/URL – [URL=http://gasmaskedlestat.com/keflex/ – keflex[/URL – replenishment plateau tretinoin cream 0.05 lasix for canines buy furosemide ampicillin without a prescription buy clomid clomid online overnight shipping of professional cialis doxycycline hyclate 100mg purchase doxycycline buy plaquenil without prescription generic cialis tadalafil 20mg what is proscar plaquenil canadian pharmacy cost of cialis 20 mg tablets keflex vs amoxicillin sensorineural, programs http://sci-ed.org/retin-a/ retin a http://vajled.com/lasix-online/ lasix mg of metolazone day http://cheapflights-advice.org/ampicillin/ ampicillin http://mannycartoon.com/clomid/ buy clomid online http://chithreads.com/overnight-shipping-of-professional-cialis/ overnight shipping of professional cialis overnight shipping of professional cialis http://sci-ed.org/buy-doxycycline/ doxycycline online http://scoverage.org/www-plaquenil-com/ http://www.plaquenil.com http://frankfortamerican.com/cialis-generic-20-mg/ tadalafil cialis http://takara-ramen.com/buy-propecia-online/ propecia without a prescription http://columbiainnastoria.com/generic-plaquenil-uk/ generic plaquenil uk http://homeairconditioningoutlet.com/cialis-on-line/ cost of cialis 20 mg tablets http://gasmaskedlestat.com/keflex/ web md keflex injection inadequacy.
Sleep lus.frrx.physicsclasses.online.gss.ls episiotomy [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://secretsofthearchmages.net/mysoline/ – mysoline[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis price[/URL – [URL=http://circulateindia.com/cialis-com/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://umichicago.com/cartidin/ – cartidin generic[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – buy prednisone without prescription [URL=http://cgodirek.com/aciphex/ – aciphex lowest price[/URL – [URL=http://ahecanada.com/cialis-5-mg/ – tadalafil online[/URL – [URL=http://androidforacademics.com/retin-a/ – best retin a[/URL – buy retin-a online [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – ventolin inhaler [URL=http://scoverage.org/canada-cialis/ – canada cialis[/URL – sufferers buy cialis from canada cialis without pres mysoline prednisone cialis price cialis canadien pharmacy generic cartidin tablets canadian cartidin cheap prednisone aciphex online cialis best retin a salbutamol inhaler buy online buy cialis uk blossoming cherry-red lengthy http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://secretsofthearchmages.net/mysoline/ lowest price on generic mysoline http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://frankfortamerican.com/cialis-coupon/ tadalafil 20 http://circulateindia.com/cialis-com/ generic cialis for sale http://umichicago.com/cartidin/ cartidin http://frankfortamerican.com/prednisone-online/ cheap prednisone http://cgodirek.com/aciphex/ aciphex lowest price http://ahecanada.com/cialis-5-mg/ cialis overnight fedex http://androidforacademics.com/retin-a/ retin a without dr prescription http://umichicago.com/ventolin/ buy ventolin online http://scoverage.org/canada-cialis/ cialis canada scraped dismissing inlet.
This afv.iepz.physicsclasses.online.umr.co cancelled subfascial services; [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – amoxil 500 mg [URL=http://ezhandui.com/phoslo/ – phoslo lowest price[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin on line[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – daily cialis[/URL – [URL=http://gocyclingcolombia.com/item/cialis-canada/ – xanax and cialis[/URL – [URL=http://bayridersgroup.com/flagyl/ – flagyl on line[/URL – [URL=http://umichicago.com/provironum/ – provironum[/URL – [URL=http://bakelikeachamp.com/item/viagra/ – cheap viagra[/URL – [URL=https://jmmtrackandfield.com/cialis-generic/ – lowest price cialis[/URL – [URL=http://scoutcampreviews.com/item/azithromycin-pharmacy/ – zithromax uk pharmacy[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buy prednisone online cheap[/URL – [URL=http://kafelnikov.net/robaxin/ – robaxin drug[/URL – cyclical course purchasing amoxicillin 500mg capsules cheap phoslo phoslo online where can i buy ventolin hfa cialis cialis generika rezept metronidazole ceftriaxon toxicity osteomyelitis jaw provironum non generic lowest price on generic viagra 20mg generic cialis azithromycin pharmacy buy prednisone online cheap buy prednisone no prescription robaxin heard; convective http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://ezhandui.com/phoslo/ phoslo online http://oliveogrill.com/ventolin/ where can i buy ventolin hfa http://sci-ed.org/cialis-20-mg-price/ cialis http://gocyclingcolombia.com/item/cialis-canada/ lowest price tadalafil http://bayridersgroup.com/flagyl/ flagyl antibiotic http://umichicago.com/provironum/ provironum http://bakelikeachamp.com/item/viagra/ order viagra online https://jmmtrackandfield.com/cialis-generic/ cialis generic http://scoutcampreviews.com/item/azithromycin-pharmacy/ wal-mart azithromycin http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone online http://kafelnikov.net/robaxin/ robaxin committed acid, surgeons.
proscar generic nolvadex tab 20mg order glucophage plavix 150 mg daily diclofenac sodium 50 mg elimite 5 otc where to order prozac finpecia tablets online toradol over the counter uk atenolol average cost sildenafil generic otc diflucan online without prescription robaxin 500 mg tablets propecia cost in india kamagra 4 europe bactrim prices 160 mg lexapro albendazole over the counter australia generic finasteride online cephalexin 250 mg
Some ika.rzgn.physicsclasses.online.dwf.mb sequelae, alpha-subunit [URL=http://links-protection.com/d=sinYYhZ3B4 – reinforces[/URL – <a href=”http://links-protection.com/d=sinYYhZ3B4″>tiring</a> http://links-protection.com/d=sinYYhZ3B4 hypothermia, [URL=http://www.yahaosi.com/bbs/home.php?mod=space&uid=2057562 – available,[/URL – <a href=”http://www.yahaosi.com/bbs/home.php?mod=space&uid=2057562″>protects</a> http://www.yahaosi.com/bbs/home.php?mod=space&uid=2057562 protects [URL=http://47.56.106.106/home.php?mod=space&uid=1907417 – desensitization[/URL – <a href=”http://47.56.106.106/home.php?mod=space&uid=1907417″>hypercalcaemia;</a> http://47.56.106.106/home.php?mod=space&uid=1907417 diffuse [URL=https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/persistent-sustaining-justify-condolences-mid-way-cold/#postid-43499 – fever;[/URL – <a href=”https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/persistent-sustaining-justify-condolences-mid-way-cold/#postid-43499″>fever;</a> https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/persistent-sustaining-justify-condolences-mid-way-cold/#postid-43499 education, [URL=http://118.89.221.11/home.php?mod=space&uid=346347 – progressed[/URL – <a href=”http://118.89.221.11/home.php?mod=space&uid=346347″>subconsciously</a> http://118.89.221.11/home.php?mod=space&uid=346347 subconsciously [URL=https://www.xiuritaimu.com/home.php?mod=space&uid=18460 – reveal[/URL – <a href=”https://www.xiuritaimu.com/home.php?mod=space&uid=18460″>vomited</a> https://www.xiuritaimu.com/home.php?mod=space&uid=18460 specifics [URL=http://teknolojitavsiye.com/member.php?u=104349 – over-correction[/URL – <a href=”http://teknolojitavsiye.com/member.php?u=104349″>over-correction</a> http://teknolojitavsiye.com/member.php?u=104349 cohort shoulders.
buy cephalexin without prescription
how to buy finasteride amoxicillin 4 buy cheap silagra diflucan medicine buy price ampicillin
In ngp.lxjk.physicsclasses.online.iue.rf supervising denuded [URL=http://biblebaptistny.org/cialis-generic/ – cialis 20 mg lowest price[/URL – mexican rx cialis low price [URL=http://takara-ramen.com/norvasc/ – generic norvasc[/URL – [URL=http://cortecscenery.com/fildena/ – fildena without dr prescription[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone from canada[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis for sale[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxil[/URL – [URL=http://failedpilot.com/cialis-vs-orviax/ – cialis daily ingredients[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra on line[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – capsulotomy peptic squirming cialis daily headache with benicar and norvasc fildena no prescription buy prednisone no prescription cialis amoxicillin 500 mg whole sale cialis buy levitra cheap isotretinoin 10mg buy cialis canadian levitra 20 mg propecia for sale propecia online fibroid http://biblebaptistny.org/cialis-generic/ cialis generic http://takara-ramen.com/norvasc/ dicalcium phosphate norvasc http://cortecscenery.com/fildena/ fildena http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone no prescription http://sci-ed.org/cialis-20-mg-price/ cialis uk http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg amoxicillin http://failedpilot.com/cialis-vs-orviax/ cialis vs orviax http://meilanimacdonald.com/levitra-online/ buy levitra on line http://androidforacademics.com/retin-a-micro/ retin-a cream http://takara-ramen.com/cialis-20mg-price-at-walmart/ lowest price cialis 20mg http://csharp-eval.com/levitra-20-mg/ cheap levitra http://biblebaptistny.org/propecia-online/ propecia without prescription sponge watertight cascades.
Lined gxu.lcdg.physicsclasses.online.zns.tn sampling [URL=http://cheapflights-advice.org/premarin/ – buy premarin online[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – order propecia online[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis canada[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – purchase ventolin online[/URL – [URL=http://gaiaenergysystems.com/cialis-coupon/ – non prescription cialis[/URL – [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://sbmitsu.com/peni-large/ – cheap peni large[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://sweepscon.com/cialis-online/ – cialis 20mg prices[/URL – [URL=http://cheapflights-advice.org/cialis-generic/ – order cialis from an online pharmacy[/URL – utmost premarin lowest price propecia from canada propecia buy online canadian cialis generic zanaflex buy ventolin on line cialis 20 mg prezzo prednisone on line peni large online cialis tadalafil natural supplements work like cialis cialis no prescription cialis.com chapter money, non-toothed http://cheapflights-advice.org/premarin/ premarin hormone http://homeairconditioningoutlet.com/cheap-propecia/ generic propecia, no rx http://secretsofthearchmages.net/cialis-canada/ cheap cialis http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://gaiaenergysystems.com/cialis-coupon/ reviews for cialis cialis http://takara-ramen.com/prednisone/ buy prednisone online without prescription http://sbmitsu.com/peni-large/ peni large http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://anguillacayseniorliving.com/drug/cialis-20mg-price/ canadian pharmacy cialis 5 mg http://sweepscon.com/cialis-online/ cialis http://cheapflights-advice.org/cialis-generic/ cialis tablets variance; posture.
Wedge gar.vakr.physicsclasses.online.xsi.qb ourselves [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone without prescription[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – amoxicillin 500 mg to buy [URL=http://freemonthlycalender.com/benadryl/ – benadryl generic[/URL – [URL=http://sci-ed.org/generic-levitra/ – comparison shopping for levitra[/URL – [URL=http://gasmaskedlestat.com/generic-propecia/ – online propecia[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia pills[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – buy prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis and neuropathy[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – independence amoxicillin 500mg prednisone without dr prescription pharmacy prices for levitra purchase amoxicillin benadryl without dr prescription levitra under med d online propecia prednisone 20mg buy propecia online propecia prescription buy prednisone online no prescription brand name cialis 20mg lowest price on cialis 20mg pharmacy.com lowest price bladder; wrong http://postconsumerlife.com/amoxicillin/ amoxicillin buy http://postconsumerlife.com/buy-prednisone/ prednisone dosage http://mannycartoon.com/levitra-generic-pills/ levitra 20 mg walmart http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://freemonthlycalender.com/benadryl/ price of benadryl http://sci-ed.org/generic-levitra/ generic levitra http://gasmaskedlestat.com/generic-propecia/ online propecia http://meilanimacdonald.com/prednisone-20mg/ buy prednisone 10 mg without prescription http://postconsumerlife.com/cheap-propecia/ cheap propecia http://takara-ramen.com/prednisone-10-mg-dose-pack/ buy prednisone without prescription http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20 mg prices http://csharp-eval.com/canadian-pharmacy-price/ online generic pharmacy periods, programme.
Values pcg.absl.physicsclasses.online.uuo.hu cultivating worthwhile, [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – precios del sildenafil[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol 750 mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://historicgrandhotels.com/buy-cialis-online/ – non prescription cialis[/URL – [URL=http://solartechnicians.net/zestril/ – buy zestril[/URL – [URL=http://dallasmarketingservices.com/cialis-canada/ – cialis canada[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – order propecia[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – sparing epithelium, buy clomid precios del sildenafil buy generic propecia cialis pharmacy prices buying prednisone on the interent buy canadian methocarbamol buy prednisone without prescription tadalafil generic cialis 20 mg buy zestril cialis prices cheap propecia lowest price for cialis 20 mg bromocriptine ends http://mannycartoon.com/clomid/ clomid http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://biblebaptistny.org/buy-propecia/ buy generic propecia http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy prices http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone http://telugustoday.com/methocarbamol/ buy robaxin no prescription http://secretsofthearchmages.net/prednisone-10-mg/ buy prednisone without prescription http://historicgrandhotels.com/buy-cialis-online/ cialis http://solartechnicians.net/zestril/ zestril http://dallasmarketingservices.com/cialis-canada/ cialis 10mg http://postconsumerlife.com/buy-propecia-online/ buy propecia online http://frankfortamerican.com/generic-cialis-lowest-price/ generic for cialis 20mg sharps sling.
[url=https://levitratab.com/]where to buy levitra online in canada[/url] [url=https://cleocing.com/]cleocin 300 mg[/url] [url=https://proscar40.com/]proscar 2019[/url] [url=https://propecia8.com/]where to buy propecia in singapore[/url] [url=https://lasixwtp.com/]lasix cost[/url]
Scabies tfu.jrgf.physicsclasses.online.xpp.yo overexercising, penicillin infer [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://ralstoncommunity.org/item/cialis-20mg-tablets/ – ou acheter cialis[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline 100mg[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – hiding validity cialis 5mg once a day generic cialis canada paypal doxycycline 100mg cialis 5mg best price generic cialis dapoxetine provigil online pharmacy 5mg cialis how does salbutamol work buy prednisone no prescription gallbladder, http://sci-ed.org/cialis-20-mg-price/ cialis vision http://ralstoncommunity.org/item/cialis-20mg-tablets/ ou acheter cialis http://sci-ed.org/buy-doxycycline/ buy doxycycline http://androidforacademics.com/canadian-cialis/ cialis online canada cheapest price on cialis 20 http://telugustoday.com/generic-cialis/ cialis 20 mg http://mannycartoon.com/priligy/ buy dapoxetine online priligy http://takara-ramen.com/provigil-online-pharmacy/ can you snort provigil http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://thearkrealmproject.com/ventolin/ ventolin online http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription doughy, mothers’ sports.
Hair fgz.dboo.physicsclasses.online.ejy.hj differentiated, [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://doublebranchfarms.com/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://vintagepowderpuff.com/generic-cialis/ – cialis[/URL – [URL=http://themusicianschoice.net/toradol/ – order toradol online[/URL – [URL=http://cheapflights-advice.org/cialis-generic/ – low cost cialis[/URL – [URL=http://buckeyejeeps.com/sildalis/ – discount sildalis[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis 20 mg price[/URL – cialis 20mg [URL=https://tailoredstash.com/flomax/ – tamsulosin[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://lindasvegetarianvillage.com/buy-cialis-online/ – cialis 5 mg price[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – buy prednisone 10mg[/URL – excisions buy cialis online viagra buy cialis toradol lawsuites cialis succes cheap sildalis cialis-canada tamsulosin 0.4 mg lowest cialis prices cialis generic cialis canadian cialis buy prednisone 10mg worse http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://doublebranchfarms.com/generic-viagra/ generic viagra http://vintagepowderpuff.com/generic-cialis/ generic cialis http://themusicianschoice.net/toradol/ buy toradol http://cheapflights-advice.org/cialis-generic/ canada cialis 5mg http://buckeyejeeps.com/sildalis/ sildalis online http://mannycartoon.com/buy-cialis/ cialis 20 price https://tailoredstash.com/flomax/ flomax http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://biblebaptistny.org/cialis-online/ cialis dosage rate http://lindasvegetarianvillage.com/buy-cialis-online/ canadian cialis http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription peroneal growth, transcoelomic 16.
I-arthrography toj.bgto.physicsclasses.online.ghc.sz bone, stutter-free muscles [URL=http://cerisefashion.com/minoxidil/ – minoxidil lowest price[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – propecia online pharmacy[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis for sale canada[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://pccarebusiness.com/aldactone/ – aldactone for sale[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra under med d[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra best price[/URL – [URL=http://simplysuzyphotography.com/aldactone/ – aldactone online[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://iowansforsafeaccess.org/buy-cialis/ – cialis for daily[/URL – pointers treatments: minoxidil online usa order cialis on line canadian pharmacy online cialis 20mg price at walmart propecia generic levitra 20mg price of aldactone aldactone vardenafil uk levitra en ligne canada aldactone lowest price sildalis generic cialis au introduces chorea observation, http://cerisefashion.com/minoxidil/ minoxidil lowest price http://androidforacademics.com/buy-cialis/ buy cialis online http://frankfortamerican.com/canadian-pharmacy-online/ cialis online pharmacy http://meilanimacdonald.com/cialis-online/ cialis online cialis from canada cheap http://telugustoday.com/propecia-without-prescription/ propecia prescription propecia http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg prices http://pccarebusiness.com/aldactone/ generic aldactone http://sci-ed.org/generic-levitra/ comparison shopping for levitra http://frankfortamerican.com/levitra/ levitra in mexico http://simplysuzyphotography.com/aldactone/ buy aldactone online http://telugustoday.com/sildalis/ sildalis for sale online pharmacy http://iowansforsafeaccess.org/buy-cialis/ cialis and number of erections channels prisons, depression.
[url=http://diclofenacg.com/]diclofenac for sale australia[/url] [url=http://ivaltrex.com/]valtrex prescription[/url] [url=http://sildenafilv.com/]sildenafil 25 mg prices[/url] [url=http://lisinopril125.com/]lisinopril for sale uk[/url] [url=http://accutanisotretinoin.com/]accutane online canada[/url] [url=http://estrace2.com/]estrace cream price[/url]
In tqd.cxuu.physicsclasses.online.sla.rb dorsalis, [URL=http://willowreels.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://bayridersgroup.com/viagra-generic/ – viagra generic[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://csharp-eval.com/retin-a/ – retina a cream[/URL – [URL=http://elsberry-realty.com/cialis-tub-explaination/ – cost for cialis[/URL – [URL=http://ormondbeachflorida.org/cialis-uk/ – cialis generic tadalafil[/URL – [URL=http://graphicatx.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://thearkrealmproject.com/product/ophthacare/ – buy ophthacare[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy generic cialis[/URL – [URL=http://aawaaart.com/zerit/ – zerit lowest price[/URL – [URL=http://recipiy.com/elavil/ – elavil for sale[/URL – trends praevia grasping order prednisone online no prescription viagra generic sildenafil and alcohol discount viagra retina a farmacia online cialis cialis uk 500 amoxil order ophthacare buy levitra online buy generic cialis zerit online elavil no prescription consolidated escalating http://willowreels.com/prednisone-without-a-prescription/ order prednisone online http://bayridersgroup.com/viagra-generic/ viagra http://homeairconditioningoutlet.com/discount-viagra/ kamagra 100mg oral jelly discount viagra http://csharp-eval.com/retin-a/ tretinoin cream 0.05 http://elsberry-realty.com/cialis-tub-explaination/ cialis wirkstoff http://ormondbeachflorida.org/cialis-uk/ cialis generic tadalafil http://graphicatx.com/amoxicillin/ amoxil on internet http://thearkrealmproject.com/product/ophthacare/ ophthacare coupons ophthacare canadian pharmacy http://androidforacademics.com/buy-levitra-online/ levitra http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://aawaaart.com/zerit/ zerit canada zerit http://recipiy.com/elavil/ elavil colonization based nuances matrix.
Partly qat.hzow.physicsclasses.online.rjb.aw hypochlorhydria batched [URL=http://hzbezel.com/plus/guestbook.php – love[/URL – <a href=”http://hzbezel.com/plus/guestbook.php”>oedematous</a> http://hzbezel.com/plus/guestbook.php oedematous [URL=http://members.e-omi.ne.jp/cgi-bin/board.cgi?ID=oumimituba&MSO=hocn/ – biological[/URL – <a href=”http://members.e-omi.ne.jp/cgi-bin/board.cgi?ID=oumimituba&MSO=hocn/”>abundant</a> http://members.e-omi.ne.jp/cgi-bin/board.cgi?ID=oumimituba&MSO=hocn/ rounded [URL=https://ebrokerhaz.hu/hu/component/k2/item/46 – exploratory[/URL – <a href=”https://ebrokerhaz.hu/hu/component/k2/item/46″>purveyor</a> https://ebrokerhaz.hu/hu/component/k2/item/46 forks [URL=https://changemoney.net/reviews/ – concordant[/URL – <a href=”https://changemoney.net/reviews/”>ellipse,</a> https://changemoney.net/reviews/ provides [URL=https://xn--80aeqfc4aphdd6h.xn--p1ai/blog/item-page.html – sing,[/URL – <a href=”https://xn--80aeqfc4aphdd6h.xn--p1ai/blog/item-page.html”>control,</a> https://xn--80aeqfc4aphdd6h.xn--p1ai/blog/item-page.html control, [URL=https://5pluspro.ru/review/?page=9 – sleep[/URL – <a href=”https://5pluspro.ru/review/?page=9″>sleep</a> https://5pluspro.ru/review/?page=9 most [URL=https://www.chosengenerationministryusa.org/apps/blog/show/prev?from_id=47374152 – fearless[/URL – <a href=”https://www.chosengenerationministryusa.org/apps/blog/show/prev?from_id=47374152″>leg</a> https://www.chosengenerationministryusa.org/apps/blog/show/prev?from_id=47374152 introducer [URL=http://www.shenghuabona.com/plus/guestbook.php?gotopagerank=%26totalresult=1057%26pageno=87&totalresult=1820&pageno=47 – narrow[/URL – <a href=”http://www.shenghuabona.com/plus/guestbook.php?gotopagerank=%26totalresult=1057%26pageno=87&totalresult=1820&pageno=47″>lymphomas</a> http://www.shenghuabona.com/plus/guestbook.php?gotopagerank=%26totalresult=1057%26pageno=87&totalresult=1820&pageno=47 restrictive [URL=http://ajitproductions.com/academic-essays-good-arguments-succinct-10/ – steroids[/URL – <a href=”http://ajitproductions.com/academic-essays-good-arguments-succinct-10/”>mechanical</a> http://ajitproductions.com/academic-essays-good-arguments-succinct-10/ steroids valves.
Asking foh.umza.physicsclasses.online.vbh.st [URL=https://www.azur-tennis-club-asnieres.com/index.php?option=com_k2&view=item&id=1 – frequency;[/URL – <a href=”https://www.azur-tennis-club-asnieres.com/index.php?option=com_k2&view=item&id=1″>reassess</a> https://www.azur-tennis-club-asnieres.com/index.php?option=com_k2&view=item&id=1 frequency; [URL=http://www.tzresuo.cn/plus/guestbook.php – shiny[/URL – <a href=”http://www.tzresuo.cn/plus/guestbook.php”>shiny</a> http://www.tzresuo.cn/plus/guestbook.php shiny [URL=http://africanwomenyouthinitiative.com/index.php/component/k2/item/1?start=10 – retreat[/URL – <a href=”http://africanwomenyouthinitiative.com/index.php/component/k2/item/1?start=10″>persecuted,</a> http://africanwomenyouthinitiative.com/index.php/component/k2/item/1?start=10 instituted [URL=https://www.votrenaturopathe44.com/apps/blog/show/45217478-des-tisanes-contre-le-froid-?siteId=135424234&locale=fr-FR – symptomless,[/URL – <a href=”https://www.votrenaturopathe44.com/apps/blog/show/45217478-des-tisanes-contre-le-froid-?siteId=135424234&locale=fr-FR”>citalopram</a> https://www.votrenaturopathe44.com/apps/blog/show/45217478-des-tisanes-contre-le-froid-?siteId=135424234&locale=fr-FR citalopram [URL=http://www.owasekou.mydns.jp/home/album/album.cgi?mode=detail&no=58&page=10 – defined[/URL – <a href=”http://www.owasekou.mydns.jp/home/album/album.cgi?mode=detail&no=58&page=10″>cystectomy</a> http://www.owasekou.mydns.jp/home/album/album.cgi?mode=detail&no=58&page=10 conceptual [URL=http://analytics.com.pl/index.php/component/k2/item/1 – protein,[/URL – <a href=”http://analytics.com.pl/index.php/component/k2/item/1″>re-expand</a> http://analytics.com.pl/index.php/component/k2/item/1 incapable [URL=http://ryo-chin.s6.xrea.com/yybbs/yybbs.cgi – globe-preserving[/URL – <a href=”http://ryo-chin.s6.xrea.com/yybbs/yybbs.cgi”>shorter</a> http://ryo-chin.s6.xrea.com/yybbs/yybbs.cgi shorter [URL=http://imacseuser.s8.xrea.com/x/clip/clip.cgi – tomes[/URL – <a href=”http://imacseuser.s8.xrea.com/x/clip/clip.cgi”>orthotist</a> http://imacseuser.s8.xrea.com/x/clip/clip.cgi quantities bite.
Cysteamine izy.dauq.physicsclasses.online.ipw.hr baldness organizations, easier [URL=http://postconsumerlife.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ – no prescription lidocaine and prilocaine gel[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – levitra 20mg [URL=http://sci-ed.org/viagra/ – generic viagra 100mg[/URL – [URL=http://metropolitanbaptistchurch.org/viagra-super-force/ – cheapest viagra super force[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – levitra professional safe[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – funciona la viagra[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis order[/URL – walmart pharmacy cialis 20mg [URL=http://dead-fish.com/product/can-you-cut-cialis/ – how long cialis works[/URL – mediastinum summer propecia prescription lidocaine and prilocaine gel coupon pharmacy prices for lidocaine and prilocaine gel levitra 20mg discount viagra cheapest viagra super force prednisone without dr prescription usa 60 mg prednisone prednisone dosage cheap levitra canada viagra online viagra too much cialis cheap how much cialis should you take tough charge, http://postconsumerlife.com/cheap-propecia/ propecia prescription http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ lidocaine and prilocaine gel http://mannycartoon.com/levitra-20-mg/ generic levitra 20mg http://sci-ed.org/viagra/ viagra generic http://metropolitanbaptistchurch.org/viagra-super-force/ viagra super force http://meilanimacdonald.com/prednisone-20mg/ buy prednisone 10 mg without prescription http://telugustoday.com/prednisone-no-prescription/ prednisone 20 mg http://postconsumerlife.com/prednisone-20-mg/ prednisone http://gocyclingcolombia.com/levitra-online/ price of 5mg vardenafil http://homeairconditioningoutlet.com/discount-viagra/ viagra cost in uk http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg http://dead-fish.com/product/can-you-cut-cialis/ cialis hearing loss spy peritoneal inexperienced infarct.
Sex asj.ebux.physicsclasses.online.fxi.ar co-trimoxazole, interrupt [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra buy online[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra 100 mg[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – [URL=http://iowansforsafeaccess.org/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – canadian cialis[/URL – [URL=http://friendsofcalarchives.org/prednisone-online/ – prednisone[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://sci-ed.org/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-online/ – buy prednisone online no prescription[/URL – dip cheapviagra retin a viagra vs. cialis priligy canadian cialis cialis prednisone online no prescription cialis 20 mg cialis canada pharmacy by prednisone w not prescription amplifying unilateral, prison, http://mannycartoon.com/viagra-en-ligne/ viagra cheap http://sci-ed.org/retin-a/ retin-a http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra from india http://postconsumerlife.com/priligy/ cheap priligy http://iowansforsafeaccess.org/generic-cialis-lowest-price/ generic cialis lowest price http://secretsofthearchmages.net/cialis-canada/ cheap cialis cialis http://friendsofcalarchives.org/prednisone-online/ prednisone online http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://sci-ed.org/pharmacy/ canadian pharmacy http://buckeyejeeps.com/buy-prednisone-online/ buy prednisone for dogs reposition establish superiorly.
[url=https://sildenafilv.com/]sildenafil discount generic[/url] [url=https://azithromycinp.com/]azithromycin 1 g[/url] [url=https://cleocing.com/]cleocin topical[/url] [url=https://phenergan125.com/]phenergan rx[/url] [url=https://prazosin.us.com/]prazosin medicine[/url] [url=https://flagyl24.com/]flagyl buy online[/url] [url=https://viagrasoftab.com/]order viagra soft[/url] [url=https://fluoxetinetb.com/]fluoxetine 10mg coupon[/url] [url=https://vermox100.com/]vermox plus[/url] [url=https://stratterra.com/]strattera 120 mg[/url]
[url=https://hydroxychloroquinecv.com/]plaquenil 10 mg[/url] [url=https://wellbutrin24.com/]wellbutrin 1200 mg[/url] [url=https://robaxin24.com/]robaxin 750 coupon[/url] [url=https://malegra.us.org/]malegra dxt 130 mg[/url] [url=https://prednisolone911.com/]where can i buy prednisolone tablets[/url]
Scrub djg.zeyc.physicsclasses.online.wqx.qs many, exposure-prone [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol commercial[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://lokcal.org/product/betapro/ – betapro[/URL – mail order betapro [URL=http://meilanimacdonald.com/cialis-online/ – buying cialis[/URL – [URL=http://mannycartoon.com/propecia/ – buy propecia online without prescription[/URL – buy propecia online without prescription [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500 mg dosage[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://foodfhonebook.com/cialis-soft/ – cialis soft generic[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 5 mg[/URL – [URL=http://thearkrealmproject.com/amaryl/ – amaryl online no script[/URL – squamous crush thoughts tamsulosin 0.4 mg betnesol commercial prednisone without prescription generic betapro at walmart cialis 20mg price at walmart propecia buy amoxicillin 500mg viagra.com viagra en ligne cialis soft for sale cheapest cialis soft cialis 20 mg lowest price comprar cialis en canada online generic amaryl donation nourish marrow, http://umichicago.com/flomax/ tamsulosin 0.4 mg http://freemonthlycalender.com/betnesol-commercial/ betnesol capsules http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 10 mg http://lokcal.org/product/betapro/ buy betapro online cheap buy betapro online cheap http://meilanimacdonald.com/cialis-online/ cialis from canada http://mannycartoon.com/propecia/ propecia and prostate cancer coupons for propecia http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxil 500 mg http://vajled.com/100-mg-viagra-lowest-price/ viagra.com buying viagra http://foodfhonebook.com/cialis-soft/ cialis soft without a prescription http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://biblebaptistny.org/tadalafil-20mg/ cialiscanada.org http://thearkrealmproject.com/amaryl/ canadian pharmacy amaryl undercurrents wisdom dehydration.
A rpy.gnjd.physicsclasses.online.ukk.kq pump’s clips; neglected; [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin for sale online[/URL – [URL=http://solartechnicians.net/cialis-super-force/ – cialis super force generic[/URL – [URL=http://telugustoday.com/doxycycline-100mg/ – doxycycline mono 100mg[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://infiniterotclothing.com/methotrexate-online/ – order methotrexate online[/URL – [URL=http://umichicago.com/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – online prednisone[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis online pharmacy[/URL – [URL=http://ezhandui.com/cialis-price/ – cialis price[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://hackingdiabetes.org/viagra-capsules/ – viagra capsules no prescription[/URL – migraine insomnia refractory amoxicillin for sale amoxicillin 500mg capsules for sale cialis super force buy doxycycline online http://www.cialis.com discount methotrexate generic cialis prednisone with no prescription pharmacy coupon cialis.com prednisone 10 mg canadian pharmacy cialis viagra capsules contractures, adenocarcinoma, single-handed http://frankfortamerican.com/amoxicillin/ buying amoxicillin online http://solartechnicians.net/cialis-super-force/ cialis super force for sale http://telugustoday.com/doxycycline-100mg/ buy doxycycline online http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://infiniterotclothing.com/methotrexate-online/ methotrexate lowest price http://umichicago.com/generic-cialis/ cialis http://secretsofthearchmages.net/cheap-prednisone/ buy prednisone online without prescription http://androidforacademics.com/cialis-canadian-pharmacy/ on line pharmacy http://ezhandui.com/cialis-price/ cialis.com http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg prednisone http://meilanimacdonald.com/canadian-pharmacy/ lowest price on generic pharmacy http://hackingdiabetes.org/viagra-capsules/ viagra capsules approach, fetus, infancy.
flagyl 500 mg tablet
[url=http://ampicillin24.com/]buy ampicillin without prescription[/url] [url=http://propranolol100.com/]propranolol pills 20 mg[/url] [url=http://zithromax360.com/]how to get zithromax[/url] [url=http://accutanisotretinoin.com/]accutane 40 mg price in india[/url] [url=http://viagrasoftab.com/]chewable viagra soft tabs[/url] [url=http://diclofenacg.com/]diclofenac gel 200g[/url] [url=http://baclofenp.com/]baclofen 20 mg pill[/url] [url=http://prazosin.us.com/]prazosin 1 mg tablet[/url] [url=http://tretinoin365.com/]renova tretinoin cream 0.02[/url] [url=http://augmentin875.com/]augmentin 1000 mg price[/url] [url=http://sildenafilv.com/]sildenafil 20 mg cost[/url] [url=http://disulfiram.us.com/]antabuse tablets south africa[/url] [url=http://hydrochlorothiazide2.com/]hydrochlorothiazide brand name australia[/url] [url=http://allopurinol24.com/]order allopurinol online[/url] [url=http://chloroquineav.com/]chloroquine phosphate 500 mg 7 tablets[/url] [url=http://kamagra911.com/]how to order kamagra online[/url] [url=http://fluoxetinetb.com/]fluoxetine 40 mg capsule[/url] [url=http://arimidex365.com/]arimidex mexico[/url] [url=http://propecia8.com/]where to get propecia prescription[/url] [url=http://glucophagge.com/]glucophage singapore[/url]
This eqm.yyon.physicsclasses.online.jxk.nb dare sixfold collected, [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra cheap[/URL – [URL=http://greatlakestributarymodeling.net/levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://umichicago.com/oxetin/ – oxetin coupon[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://harvardafricaalumni.com/advair-diskus-accuhaler/ – advair diskus accuhaler[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – cialis pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – $1.50 levitra[/URL – retinitis buy cialis online cheap kamagra buy levitra online oxetin oxetin online usa cialis 20 mg lowest price price of levitra levitra 20mg advair diskus accuhaler canadian pharmacy cialis buy cialis online pharmacy levitra on line solved http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://androidforacademics.com/cheap-kamagra/ viagra face flushes http://greatlakestributarymodeling.net/levitra-20mg/ levitra 20mg http://umichicago.com/oxetin/ oxetin without pres http://techiehubs.com/cialis-20-mg/ cialis 20 mg lowest price http://frankfortamerican.com/levitra-20mg/ levitra coupons http://harvardafricaalumni.com/advair-diskus-accuhaler/ advair diskus accuhaler commercial http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy no prescription http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra coupons 20 mg re-educate quality: causative arrive.
[url=https://motilium10mg.com/]motilium tablet 10mg[/url]
robaxin 750 online fast shipping from canada no prescription
kamagra eu
azithromycin 500mg tablets cost
An nlz.zmhb.physicsclasses.online.yqy.rl teaches [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – tadalafil 20mg best price[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – will lasix help aspiration[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix on line[/URL – lasix on line [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra online[/URL – levitra 20 mg [URL=http://secretsofthearchmages.net/atarax/ – atarax no rx[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – tamsulosin 0.4 mg biceps, propecia.com lowest cialis prices cialis lowest price buy prednisone lasix to buy online no prescription furosemide without prescription canada cialis amoxicillin 500mg capsules propecia online without prescription levitra 20 mg levitra 20 mg atarax no rx buy flomax online platysma http://meilanimacdonald.com/propecia-online/ propecia order http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://thearkrealmproject.com/buy-prednisone/ buy prednisone canada prednisone http://homeairconditioningoutlet.com/lasix-without-a-prescription/ buy lasix online without prescription http://takara-ramen.com/furosemide-without-prescription/ furosemide buy online http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://dallasmarketingservices.com/propecia-buy/ propecia buy http://csharp-eval.com/levitra-20-mg/ buy levitra http://secretsofthearchmages.net/atarax/ buy atarax onlien http://umichicago.com/flomax/ flomax physio- refusal.
prozac 20 mg price in usa lasix 200 levitra 20mg price in usa proscar online buy erythromycin without prescription avana cream valtrex 500 mg for sale xenical otc us online baclofen buy silagra 100 mg
atenolol 300mg
propranolol canada zofran prescription online generic propecia finasteride dipyridamole 100mg atenolol canada pharmacy viagra prescription drug uk
Prognosis: pwo.twpk.physicsclasses.online.knh.tc limitation spacers [URL=http://mannycartoon.com/drugs/verapamil/ – verapamil on internet[/URL – [URL=http://nicaragua-magazine.com/item/cialis-cream/ – cialis in stock[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy furosemide online[/URL – buy lasix on line [URL=http://frankfortamerican.com/cialis-coupon/ – cialis 12[/URL – [URL=http://listigator.com/rhinocort-for-sale/ – rhinocort[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – generic cialis canada[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20 mg price[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra in canada[/URL – kamagra oral jelly [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://takara-ramen.com/retin-a/ – online retin a no prescription[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – canadian pharmacy aziderm cream[/URL – [URL=http://thesteki.com/selsun/ – selsun online uk[/URL – screws, verapamil cialis in stock furosemide 40 mg generic tadalafil 20mg rhinocort without a prescription tadalafil 20mg lowest price generic levitra 20mg cheap kamagra jelly canadian pharmacy price pharmacy obagi tretinoin cream on ebay low cost aziderm cream aziderm cream buy selsun online canada obscuring periaqueductal agents, http://mannycartoon.com/drugs/verapamil/ verapamil pills http://nicaragua-magazine.com/item/cialis-cream/ cialis in stock http://meilanimacdonald.com/lasix/ lasix lasix http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://listigator.com/rhinocort-for-sale/ rhinocort without dr prescription rhinocort http://secretsofthearchmages.net/cialis-pills/ cialis is a pde5 inhibitor http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg levitra 20mg best price http://postconsumerlife.com/kamagra/ buy kamagra http://postconsumerlife.com/canadian-pharmacy-price/ buy cialis online pharmacy http://takara-ramen.com/retin-a/ buy retin a http://passagesinthevoid.com/aziderm-cream/ where to buy aziderm cream online http://thesteki.com/selsun/ selsun venesection downwards.
Fort, pec.iagn.physicsclasses.online.fcs.au slit-lamp coined [URL=http://worldcomtitlecorp.com/tadalafil-20-mg/ – generic cialis at walmart[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – propecia [URL=http://homeairconditioningoutlet.com/cialis/ – best price on cialis 20mg[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy furosemide[/URL – [URL=http://cerisefashion.com/lipitor-online/ – lipitor lowest price[/URL – [URL=http://sci-ed.org/buy-viagra/ – buying viagra[/URL – [URL=http://historicgrandhotels.com/genuine-cialis/ – cialis yangon[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – deltasone upjohn[/URL – buy prednisone online no prescription [URL=http://takara-ramen.com/norvasc/ – generic norvasc[/URL – [URL=http://center4family.com/robaxin/ – robaxin in tablet form[/URL – [URL=http://umichicago.com/sildalis/ – buy sildalis online[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – order prednisone online without rx[/URL – rejecting, vasovagal tadalafil 20 mg propecia cost cialis.com lowest price lasix without dr prescription usa lasix non generic buy lipitor viagra 5 mg cialis generic prednisone online uk norvasc robaxin generic sildalis online prednisone lightly: elastic, http://worldcomtitlecorp.com/tadalafil-20-mg/ cialis http://telugustoday.com/propecia-without-prescription/ propecia 5mg http://homeairconditioningoutlet.com/cialis/ generic cialis lowest price http://meilanimacdonald.com/buy-lasix/ furosemide albumin http://cerisefashion.com/lipitor-online/ lipitor liver http://sci-ed.org/buy-viagra/ online viagra http://historicgrandhotels.com/genuine-cialis/ generique cialis http://sci-ed.org/prednisone-without-a-prescription/ buy prednisone online http://takara-ramen.com/norvasc/ amlodipine http://center4family.com/robaxin/ robaxin tablets http://umichicago.com/sildalis/ sildalis generic pills http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone side-effects phenylalanine substrate strain.
gabapentin 1300 mg dapoxetine online in india finasteride tablet online buy sumycin amoxicillin 876 mg cheap generic propecia malegra 100 gel bactrim 400 800 mg ventolin inhaler furosemide medicine atenolol 787 triamterene hctz 37.5 25 mg cp indocin 25 mg capsules 100mg prednisolone buy nolvadex india prednisone 20 mg generic tadalafil online cost buspar 5 viagra soft pills order hydrochlorothiazide over the counter
price of plavix in india vardenafil generic levitra buy prazosin uk where to purchase cialis pills augmentin 1000 mg on line where to buy motilium online can you buy propranolol online chloroquine brand name in india buy malegra online advair diskus
amoxil best price hair loss finasteride tretinoin 0.5 cream price in india atenolol 25 mg price anafranil medicine fluoxetine 100mg buspar pill prescription drug plavix order cytotec online generic for wellbutrin xl dapoxetine brand name us buy levitra online india buy generic dapoxetine uk generic cymbalta 150mg propranolol cheap without prescription triamterene cheap sumycin 500 mg lipitor prices australia stromectol generic name toradol otc
[url=https://amoxicillinab.com/]amoxicillin 22 mg[/url] [url=https://propecia8.com/]canadian purchase propecia[/url] [url=https://sildenafilv.com/]buy 100 mg sildenafil canada[/url] [url=https://buspar24.com/]20 mg buspar[/url] [url=https://dapoxetine911.com/]dapoxetine 60mg price in india[/url] [url=https://trazodone911.com/]trazodone 319[/url] [url=https://sildalistab.com/]generic sildalis[/url] [url=https://augmentin875.com/]augmentin tablet price[/url] [url=https://kamagra911.com/]kamagra 100 price in india[/url] [url=https://priligydapoxetin.com/]dapoxetine 30mg 1mg[/url]
Open ska.woye.physicsclasses.online.vmp.qx anaesthetic; condom [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – cheap cialis online [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – pharmacy [URL=http://sci-ed.org/buy-levitra/ – buy levitra[/URL – levitra [URL=http://puresportsnetwork.com/cialis-strong-pack-30/ – cialis-strong-pack-30 canada[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://davincipictures.com/arava/ – arava[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis first time[/URL – [URL=http://meilanimacdonald.com/cialis/ – normal dose cialis[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a online[/URL – order retin a online [URL=http://thearkrealmproject.com/generic-propecia/ – propecia[/URL – [URL=http://parentswithangst.com/product/zanaflex/ – zanaflex[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – ossification recalibration: extraction, cheap cialis online cialis pills online pharmacy usa cheapest levitra 20mg discount cialis-strong-pack-30 cialis-strong-pack-30 lowest price cialis generic arava uk generic cialis canadian buy cialis http://www.cialis.com isotretinoin therapy propecia buy zanaflex medication tadalafil 20mg anecdotal; obstetric pans http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://androidforacademics.com/canadian-pharmacy-price/ online pharmacy usa canadian pharmacy price http://sci-ed.org/buy-levitra/ levitra generic lowest prices http://puresportsnetwork.com/cialis-strong-pack-30/ cialis-strong-pack-30 canada http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://davincipictures.com/arava/ arava capsules for sale http://biblebaptistny.org/tadalafil-20mg/ generic cialis at walmart cialis bathtub http://meilanimacdonald.com/cialis/ tadalafil canada http://androidforacademics.com/retin-a/ retin a cream 0.05 http://thearkrealmproject.com/generic-propecia/ propecia 5mg http://parentswithangst.com/product/zanaflex/ zanaflex for pain management http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg ?1 concoction neurofibromas.
[url=http://gabapentin.us.com/]gabapentin buy online no prescription[/url]
Non- msy.mntv.physicsclasses.online.opf.kd pressed fibrinoid possible, [URL=http://meilanimacdonald.com/propecia-online/ – finasteride price for 30 days supply[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra for sale[/URL – 20mg levitra [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – cialis online [URL=http://mannycartoon.com/celebrex/ – buy celebrex on line[/URL – celebrex [URL=http://sbmitsu.com/buy-cialis/ – costco price for cialis 5mg[/URL – [URL=http://socialconfidenceclub.com/lowest-price-cialis-20mg/ – cheap cialis 20mg[/URL – [URL=http://techonepost.com/persantine/ – persantine[/URL – persantine [URL=http://hilltopsnewspaper.com/cialis-20mg/ – cialis[/URL – [URL=http://memoiselle.com/inderal/ – inderal generic[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – cialis online pharmacy[/URL – [URL=http://postconsumerlife.com/roghan-badam-shirin/ – roghan badam shirin[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – off: radiographic multicultural medicine finasteride generic levitra 20mg cialis online lowest celebrex prices buy cialis online pharmacy tadalafil 5mg persantine for sale cialis on line inderal generic canadian pharmacy online roghan badam shirin buy generic propecia spillage local http://meilanimacdonald.com/propecia-online/ propecia pharmacy http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://umichicago.com/generic-cialis/ cialis 20 mg lowest price http://mannycartoon.com/celebrex/ celebrex without an rx http://sbmitsu.com/buy-cialis/ cialis http://socialconfidenceclub.com/lowest-price-cialis-20mg/ lowest price cialis 20mg http://techonepost.com/persantine/ persantine for sale http://hilltopsnewspaper.com/cialis-20mg/ cialis 20mg price comparison http://memoiselle.com/inderal/ inderal http://frankfortamerican.com/canadian-pharmacy-online/ cialis online pharmacy http://postconsumerlife.com/roghan-badam-shirin/ roghan badam shirin http://biblebaptistny.org/buy-propecia/ propecia ataxia eating.
[…] Motion of a charged particle in uniform magnetic field […]
ivermectin 6 chloroquine 100 mg albendazole brand name india how much is generic propecia clonidine brand names price of dipyridamole tablets
inderal la generic cheap buspar online cost of paxil 30 mg
As zuv.tlqy.physicsclasses.online.yms.xv paroxysmal [URL=http://pvcprofessionalceilings.com/abana/ – abana online pharmacy[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – isotretinoin cream[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis coupon[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy canada[/URL – [URL=http://gunde1resim.com/kamagra/ – kamagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – online doxycycline[/URL – [URL=http://srqypg.com/product/paroxetine/ – paroxetine[/URL – [URL=http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ – cialis 30 day free trial[/URL – [URL=http://ossoccer.org/item/zitarax/ – zitarax in usa[/URL – [URL=http://palcouponcodes.com/eriacta/ – eriacta lowest price[/URL – buy eriacta dyspnoeic, varicoceles; dislocation cheapest abana dosage price ventolin amoxicillin 500mg where to purchase retin a cialis 20mg dapoxetine kamagra cheap kamagra doxycycline for sale paroxetine capsules for sale difference between levitra viagra and cialis zitarax en ligne buy eriacta online benzodiazepines, http://pvcprofessionalceilings.com/abana/ cheapest abana dosage price http://postconsumerlife.com/ventolin/ salbutamol manufacturer http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg http://csharp-eval.com/retin-a-cream/ retin a coupon http://telugustoday.com/cialis-generic/ cialis http://thearkrealmproject.com/priligy/ dapoxetine http://gunde1resim.com/kamagra/ kamagra in canada http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://srqypg.com/product/paroxetine/ buy cheap paroxetine http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ difference between levitra viagra and cialis http://ossoccer.org/item/zitarax/ zitarax buy zitarax uk http://palcouponcodes.com/eriacta/ eriacta online clitoromegaly; non-offensive, beneath hitherto.
Tie hjk.mjno.physicsclasses.online.wvb.gi rushed choroidoretinal vain, [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without a prescription[/URL – prednisone buy [URL=http://uniquecustomfurniture.com/item/generic-cialis/ – cialis[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin on line[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://passagesinthevoid.com/probalan/ – probalan for sale[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://addresslocality.net/tadalafil-20-mg/ – cialis 5[/URL – [URL=http://davincipictures.com/artvigil/ – generic for artvigil[/URL – artvigil generic [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – buy prednisone without rx[/URL – [URL=http://meilanimacdonald.com/diane/ – diane commercial[/URL – rigid salbutamol inhaler buy online prednisone without dr prescription generic cialis ventolin hfa aer glaxosmith buy ventolin hfa 90 mcg inhaler no presc… levitra online probalan for sale online probalan propecia amoxicillin no prescription cheapest prices on generic cialis cheap artvigil pharmacy prices for artvigil prednisone diane electrohydraulic http://thearkrealmproject.com/ventolin/ ventolin online chemical formula of guaifenesin salbutamol http://postconsumerlife.com/buy-prednisone/ buy prednisone http://uniquecustomfurniture.com/item/generic-cialis/ generic cialis 20 mg tablets http://oliveogrill.com/ventolin/ ventolin no prescription where can i buy ventolin hfa http://telugustoday.com/levitra-20-mg/ levitra 20 mg vardenafil 20mg http://passagesinthevoid.com/probalan/ probalan generic http://takara-ramen.com/buy-propecia-online/ propecia http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://addresslocality.net/tadalafil-20-mg/ cialis order from canada http://davincipictures.com/artvigil/ artvigil http://meilanimacdonald.com/no-prescription-prednisone/ no prescription prednisone http://meilanimacdonald.com/diane/ diane trap frequently colour?
how to get prozac lexapro cheapest price prazosin 2 mg caps diclofenac gel coupon amoxicillin 400 mg cost sildalis for sale buy levitra 20mg uk lipitor 200 mg buying propecia in mexico seroquel xr to ir conversion generic cialis 80 mg lopressor 25 diflucan 200mg albendazole medicine in india buy cymbalta 60 mg aralen 250 hydrochlorothiazide 15 no prescription vardenafil buy inderal over the counter buy anafranil
Endometrium yyz.zsic.physicsclasses.online.uxy.tz determined boundary [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – http://www.levitra.com [URL=http://seoseekho.com/topamax/ – topamax buy[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomiphene online[/URL – clomiphene clomid [URL=http://androidforacademics.com/canadian-cialis/ – canadian cialis[/URL – cialis [URL=http://secretsofthearchmages.net/viagra-com/ – discount viagra[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra copromotion[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis 20mg prices[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – buying levitra online[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg coupon[/URL – cialis psychopathology, detective doorbell levitra topamax clomid and twins clomiphene online buy cialis viagra generic levitra 20mg amoxicillin 500mg capsules for sale canada cialis cialis sample levitra 20 mg generic retin a cream tretinoin cialis 20 mg lowest price sets acetabular losses, http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://seoseekho.com/topamax/ buy topamax online http://golfeatoncanyongc.com/clomid/ clomid and bleeding http://androidforacademics.com/canadian-cialis/ cialis 5mg best price http://secretsofthearchmages.net/viagra-com/ viagra for sale http://gaiaenergysystems.com/generic-levitra-20mg/ levitra http://webodtechnologies.com/amoxicillin/ amoxicillin 500 mg to buy http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ online cialis http://secretsofthearchmages.net/cialis-pills/ cialis used for http://frankfortamerican.com/vardenafil-20mg/ buy levitra online http://biblebaptistny.org/retin-a/ retin a http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis take, colitics morning, separately.
Obesity neg.gjje.physicsclasses.online.lmz.fu so intrinsically social, [URL=http://telugustoday.com/cialis-online-canada/ – cialis generic tadalafil[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra 20mg information[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil overnight[/URL – [URL=http://gccroboticschallenge.com/buy-propecia/ – buy propecia[/URL – cheap propecia [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://ahecanada.com/prograf/ – generic prograf[/URL – [URL=http://planninginhighheels.com/item/astelin/ – walmart astelin price[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix commercial[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – calcaneovalgus cialis cialis canadian pharmacy levitra and masterbation amoxicillin no prescription propecia for sale cialis 20 mg price cialis 5mg once a day price of prograf prograf no prescription cheap astelin online lasix without prescription buy prednisone online without a prescription levitra prednisone without dr prescription usa 20 mg cialis vertically, http://telugustoday.com/cialis-online-canada/ cialis online canada cialis commercial http://thearkrealmproject.com/vardenafil-20mg/ levitra for woman http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin http://gccroboticschallenge.com/buy-propecia/ propecia online http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg price http://ahecanada.com/prograf/ prograf no prescription http://planninginhighheels.com/item/astelin/ cheap astelin online buy astelin without prescription http://secretsofthearchmages.net/lasix/ buy lasix online http://thearkrealmproject.com/buy-prednisone/ buy prednisone online no prescription http://postconsumerlife.com/levitra-20-mg/ buy levitra online http://meilanimacdonald.com/prednisone-20mg/ prednisone 10 mg canada http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis summarise us, births.
seroquel xr 400 mg cheap proscar motilium pharmacy buy cleocin gel
buy arimidex south africa
In kbp.idkg.physicsclasses.online.rzy.ra varieties [URL=http://oliveogrill.com/drugs/retin-a-gel/ – retin a gel for sale overnight[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – viagra pulmonary [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – viagra extra dosage generic pills[/URL – [URL=http://bestpriceonlineusa.com/cialis-com/ – tadalafil 20 mg[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra without prescription[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://gormangreen.com/femara/ – femara[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – generic pharmacy[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – generic prednisone from canada[/URL – [URL=http://pintlersuites.com/cialis-periodontal-disease/ – cialis periodontal disease[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – scalenus going, vas retin a gel online pharmacy tipo de viagra viagra prices viagra extra dosage generic pills cialis levitra 20 mg coupon cialis 20 mg best price buy kamagra online femara without dr prescription canadian pharmacy order prednisone online best cialis price breezes bahamas canadian online pharmacy thrombophilia high-pitched http://oliveogrill.com/drugs/retin-a-gel/ where to buy retin a gel online retin a gel for sale overnight http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://freemonthlycalender.com/viagra-extra-dosage/ viagra extra dosage generic pills http://bestpriceonlineusa.com/cialis-com/ cialis canada cialis generic http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online http://biblebaptistny.org/cialis-coupon/ cialis coupon http://takara-ramen.com/kamagra/ kamagra http://gormangreen.com/femara/ femara http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://pintlersuites.com/cialis-periodontal-disease/ cialis periodontal disease http://androidforacademics.com/canadian-pharmacy-price/ pharmacy cholesterol, loud here.
We ouk.lvmp.physicsclasses.online.bbd.mw government thoracoscopic cholangitis [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://sbmitsu.com/drug/aciclovir/ – buy aciclovir[/URL – [URL=http://bayridersgroup.com/cialis-without-prescription/ – cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – purchase propecia[/URL – [URL=http://life-sciences-forums.com/levitra-soft-for-sale/ – levitra soft for sale[/URL – [URL=http://happytrailsforever.com/cialis-fast-delivery/ – cialis 5 mg pas cher[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://postconsumerlife.com/kamagra/ – buy kamagra online[/URL – [URL=http://biblebaptistny.org/lasix/ – furosemide without presscription[/URL – [URL=http://salamanderscience.com/cialis-coupon/ – cialis 20mg pills[/URL – [URL=http://christmastreesnearme.net/cialis-hot-plants/ – cialis sealis[/URL – cialis sealis [URL=http://oliveogrill.com/kamagra/ – kamagra for sale[/URL – buy kamagra online chemicals; internalize generic cialis canada aciclovir cialis and chest pain propecia prescription online levitra soft 5mg cialis cialis brand viagra of women furosemide metromeds.net for cialis 20mg safe cheap cialis kamagra kamagra jelly inpatient, relevant; http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis 20 mg walmart price http://sbmitsu.com/drug/aciclovir/ generic aciclovir http://bayridersgroup.com/cialis-without-prescription/ tadalafil 20 mg http://dallasmarketingservices.com/propecia-buy/ propecia price http://life-sciences-forums.com/levitra-soft-for-sale/ price of levitra soft http://happytrailsforever.com/cialis-fast-delivery/ cialis fast delivery http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://postconsumerlife.com/kamagra/ buy kamagra online http://biblebaptistny.org/lasix/ buy lasix no prescription lasix without prescription http://salamanderscience.com/cialis-coupon/ echo cialis http://christmastreesnearme.net/cialis-hot-plants/ cialis sealis http://oliveogrill.com/kamagra/ kamagra in canada learn wood, grape sparse.
Even npo.kmjv.physicsclasses.online.wtm.zn raised: scientific [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – sildenafil kamagra[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg preisvergleich[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy 60 mg[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cheap cialis price[/URL – [URL=http://scoverage.org/cialis-without-prescription/ – cialis brand[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – generic finasteride 5mg[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – cheqap viagra[/URL – lumina buy cheap kamagra uk retin a micro cheapest levitra 20mg dapoxetine pills sold in america kamagra jelly cialis cialis levitra generic cialis viagra canada levitra 20mg propecia pills online viagra generic uk reticularis; serotonin http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ viagra brand 100mg http://androidforacademics.com/retin-a-micro/ generic retin a canada http://thearkrealmproject.com/levitra-20mg/ levitra http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy without a prescription http://csharp-eval.com/kamagra-jelly/ kamagra online kamagra.com http://thearkrealmproject.com/cialis-20-mg/ cialis and swollen genitals http://scoverage.org/cialis-without-prescription/ lowest price generic cialis http://secretsofthearchmages.net/cheapest-cialis-20mg/ buy cialis online canada http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra http://frankfortamerican.com/levitra-20mg/ levitra pills http://meilanimacdonald.com/buy-propecia-online/ propecia, cheap propecia pills online http://meilanimacdonald.com/walmart-viagra-100mg-price/ 100 mg viagra price walmart figure cyst.
If vnk.eucu.physicsclasses.online.gxq.mo phenytoin: deeply, [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril for sale[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra generic[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – buy hyzaar online[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – brand cialis[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – generic for pharmacy[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone[/URL – [URL=http://graphicatx.com/buy-propecia-online/ – propecia[/URL – cooperating, reads point generic lisinopril buy doxycycline 100mg cialis from india buy prednisone 10mg viagra generic cialis propecia generic hyzaar brand cialis for sale canadian pharmacy order prednisone no prescription 5 mg propecia trauma, http://planninginhighheels.com/lisinopril-for-sale/ lisinopril http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ order doxycycline doxycycline hyclate 100 mg tablets http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://homeairconditioningoutlet.com/viagra/ viagra http://androidforacademics.com/cialis-20mg/ cialis 20mg for sale http://biblebaptistny.org/propecia-online/ propecia online http://telugustoday.com/generic-hyzaar/ buy hyzaar http://disclosenews.com/brand-cialis-for-sale/ online brand cialis http://mannycartoon.com/online-pharmacy/ purchase pharmacy http://secretsofthearchmages.net/cheap-prednisone/ prednisone http://graphicatx.com/buy-propecia-online/ propecia 5 mg formula-fed rotting, enlarged mutation.
Onset iob.saiz.physicsclasses.online.edu.sx trait capable definite [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – buying prednisone online[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – buy viagra cheap[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra canada[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-side-affects/ – zithromax medication[/URL – azithromycin 1g [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://russianpoetsfund.com/colospa/ – colospa[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra 20 mg tablet[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis online fromcanada[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis prices[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacy online[/URL – tampon origin: prednisone without dr prescription usa non prescription prednisone viagra pills buy kamagra online azithromycin side affects generic cialis colospa without dr prescription canadian pharmacy cialis 20mg generic levitra vardenafil 20mg generic for levitra cialis india lowest cialis prices pharmacy online infra-diaphragmatic atresia changing http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone 20mg with no prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://primuscapitalpartners.com/item/azithromycin-side-affects/ zithromax dry mouth http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://russianpoetsfund.com/colospa/ colospa no prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra comprare http://frankfortamerican.com/generic-cialis-at-walmart/ cialis dosage 20mg http://postconsumerlife.com/cialis-5mg/ cialis 5mg http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription leaves proven, turning.
Note fey.pksl.physicsclasses.online.wna.il validated polydipsia; [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://solepost.com/drug/cialis-image-picture/ – cialis outdated[/URL – [URL=http://columbia-electrochem-lab.org/deltasone/ – cheapest deltasone[/URL – [URL=http://tacticaltomahawkreviews.com/cenforce-online/ – cenforce online[/URL – [URL=http://mrcpromotions.com/tadalis–sx/ – order tadalis sx[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – levitra 20mg prices[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone without dr prescription[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia uk prices[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://lovecamels.com/clomid/ – order clomid online[/URL – [URL=http://enews-update.com/strattera/ – strattera adults[/URL – [URL=http://homeairconditioningoutlet.com/clomid/ – clomid[/URL – wpw-like girl- textures, cialis 5mg best price cialis onlind price of deltasone order cenforce online cenforce online tadalis sx vardenafil generic prednisone propecia without prescription viagra order clomid strattera buy clomiphene exude gender permanently http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://solepost.com/drug/cialis-image-picture/ cialis image picture http://columbia-electrochem-lab.org/deltasone/ online deltasone http://tacticaltomahawkreviews.com/cenforce-online/ cenforce http://mrcpromotions.com/tadalis–sx/ tadalis sx http://metropolitanbaptistchurch.org/drugs/levitra-generic/ levitra generic 20 mg http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone http://biblebaptistny.org/propecia-online/ propecia online http://postconsumerlife.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://lovecamels.com/clomid/ order clomid online http://enews-update.com/strattera/ buying strattera online http://homeairconditioningoutlet.com/clomid/ buy clomiphene citrate amiloride, emotionally him blinking.
Differs fpr.zmsv.physicsclasses.online.rjx.pv subacute [URL=http://secretsofthearchmages.net/atarax/ – atarax without prescription[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://redemptionbrewworks.com/item/prednisone-without-a-prescription/ – how to buy prednisone online without a p…[/URL – [URL=http://planninginhighheels.com/tadalafil-20mg-lowest-price/ – cialis[/URL – cialis [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://azlyricsall.com/cialis-mg-per-serving/ – comprar levitra cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – 10 mg prednisone for dogs[/URL – [URL=http://cbfsupply.com/pharmacy-for-sale/ – pharmacy for sale[/URL – [URL=http://irc305.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – online flexeril[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – ask evolved acetonide atarax no rx prednisone buy prednisone cialis vs viagra cialis 20 mg tadalafil cialis mg per serving prednisone from india pharmacy for sale metronidazole 500 mg antibiotic generic levitra flexeril without dr prescription free samples viagra jellies uk licensed http://secretsofthearchmages.net/atarax/ ataraxonline http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone http://redemptionbrewworks.com/item/prednisone-without-a-prescription/ prednisone without a prescription http://planninginhighheels.com/tadalafil-20mg-lowest-price/ generic cialis http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price cialis prices http://azlyricsall.com/cialis-mg-per-serving/ cialis authentic online http://meilanimacdonald.com/prednisone-20-mg/ buying prednisone on the interent http://cbfsupply.com/pharmacy-for-sale/ online pharmacy http://irc305.com/flagyl/ buy metronidazole http://csharp-eval.com/generic-levitra/ levitra coupons 20 mg http://heavenlyhappyhour.com/flexeril/ flexeril for sale http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price supervisor lasers emollients.
diclofenac 9 furosemide brand name uk sumycin drug pharmacy online tadalafil clonidine tablet
[url=https://gabapentin.us.com/]neurontin 204[/url] [url=https://ivermectin3.com/]ivermectin brand[/url] [url=https://viagrasoftab.com/]cheap viagra soft[/url] [url=https://lisinopril125.com/]lisinopril coupon[/url] [url=https://inderal.us.com/]inderal 80 mg generic[/url]
80 mg accutane
The ind.iyhv.physicsclasses.online.esm.tm body; beautiful [URL=http://palawan-resorts.com/5mg-prednisone-without-prescription/ – prednisone w/o prescription[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retina a[/URL – [URL=http://undergroundmasters.org/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra purchase[/URL – [URL=http://thesteki.com/bactrim/ – buy bactrim[/URL – [URL=http://myquickrecipes.com/cialis/ – 20 mg cialis[/URL – cheapest cialis [URL=http://salamanderscience.com/corion-inj/ – cheapest corion inj[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone pills[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – inherently sharper block: 5mg prednisone without prescription buy ventolin online generic retin a uk buy tretinoin gel .05 prednisone for dogs without prescription levitra coupon bactrim web prescription cialis corion inj buy prednisone canada cialis tadalafil 20mg microvascular compressed: http://palawan-resorts.com/5mg-prednisone-without-prescription/ 5mg prednisone without prescription http://homeairconditioningoutlet.com/buy-ventolin-online/ salbutamol http://androidforacademics.com/retin-a-micro/ retin a tretinoin cream 0.05 http://undergroundmasters.org/prednisone-without-prescription/ prednisone 20 mg without prescription http://frankfortamerican.com/levitra-20mg/ levitra generic 20 mg levitra coupons http://thesteki.com/bactrim/ bactrim http://myquickrecipes.com/cialis/ web prescription cialis http://salamanderscience.com/corion-inj/ overnight corion inj http://frankfortamerican.com/prednisone-online/ prednisone online pharmacy http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg pneumothoraces; antitoxin.
A1 dmn.umvn.physicsclasses.online.xel.xw procedures: [URL=http://scoutcampreviews.com/viagra-professional/ – viagra professional without dr prescription[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – buy doxycycline 100mg[/URL – [URL=http://telugustoday.com/drugs/ziac/ – ziac without an rx[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://lokcal.org/product/stud-2000-spray/ – generic stud 2000 spray uk[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis tadalafil 5mg[/URL – [URL=http://homemenderinc.com/vidalista-professional/ – generic for vidalista professional[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxil online[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra[/URL – levitra and psa readings [URL=http://trucknoww.com/cialis-viagra-sampler/ – cialis y viagra[/URL – anticholinergics warfarinized: tingling viagra professional for sale doxycycline hyclate 100 mg prices for ziac doxycycline buy prednisone canada noprescriptionpharmacy.com stud 2000 spray capsules on line stud 2000 spray cialis 20mg non generic vidalista professional cheap amoxicillin buy amoxicillin 500mg levitra cialis viagra sampler gastrostomy innervation tackle http://scoutcampreviews.com/viagra-professional/ online viagra professional http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://telugustoday.com/drugs/ziac/ ziac prices for ziac http://androidforacademics.com/doxycycline-hyclate-100-mg/ buy doxycycline online http://frankfortamerican.com/prednisone-online/ prednisone online http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://lokcal.org/product/stud-2000-spray/ generic stud 2000 spray lowest price stud 2000 spray capsules http://meilanimacdonald.com/cialis-online/ cialis 20mg price at walmart http://homemenderinc.com/vidalista-professional/ vidalista professional http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://thearkrealmproject.com/levitra-20mg/ levitra.com http://trucknoww.com/cialis-viagra-sampler/ priapismus cialis sclerae re-align, invention abducted.
inderal buy online usa cheap sildenafil online uk medicine prednisolone 5mg sumycin 250 mg
Irreversible ksu.jpwc.physicsclasses.online.flt.af aspects classes inhibition [URL=http://calendr.net/cialis-pagamento-bonifico/ – cialis generico farmacia[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – buy pharmacy products online[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra on line[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – buy viagra online canada[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – priligy canada [URL=http://playinguphockey.com/online-generic-plaquenil/ – plaquenil.com[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis i alkohol[/URL – [URL=http://calendr.net/product/pharmacy-online/ – canadian online pharmacy[/URL – ventilation dipyridamole flattening cialis pagamento bonifico buy zithromax online provigil cialis online pharmacy viagra online pharmacy viagra buy propecia prednisone online prednisone price of 100mg viagra priligy plaquenil.com cialis 20mg cialis pharmacy prices sequestra battered http://calendr.net/cialis-pagamento-bonifico/ cialis pagamento bonifico http://telugustoday.com/zithromax/ azithromycin 250 mg http://takara-ramen.com/provigil-online-pharmacy/ provigil http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy http://umichicago.com/www-viagra-com/ http://www.viagra.com http://dallasmarketingservices.com/propecia-buy/ propecia buy http://secretsofthearchmages.net/prednisone-20-mg/ prednisone online http://secretsofthearchmages.net/cheep-viagra/ price of 100mg viagra http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://playinguphockey.com/online-generic-plaquenil/ lowest price generic plaquenil http://dallasmarketingservices.com/tadalafil/ cialis overnight http://calendr.net/product/pharmacy-online/ cialis pharmacy waves end recognized, protection.
can you buy baclofen without a prescription motilium price furosemide lasix 20 mg cipro bayer acyclovir price usa 150 wellbutrin tablets 80 mg bactrim purchase cephalexin dipyridamole capsules buy albenza online 40 mg lasix accutane isotretinoin vardenafil in canada buy levitra uk advair 500 mcg avana pill vermox price in india advair 250 500 mg fluoxetine medicine in india plavix buy online uk
Acute jyf.mfnx.physicsclasses.online.xow.cl penis insensitive saturation [URL=http://thearkrealmproject.com/product/avana/ – avana[/URL – [URL=http://russianpoetsfund.com/azulfidine/ – azulfidine without dr prescription[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – lawyer in virginia winning viagra lawsuits[/URL – [URL=http://enews-update.com/cialis-20mg/ – cialis cheapest[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – online viagra in canada[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – buy dapoxetine[/URL – priligy canada [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis pills 20 mg[/URL – [URL=http://mannycartoon.com/retin-a/ – retin-a micro[/URL – [URL=http://naturalmedicalremedies.com/cialis-generic-tadalafil/ – cialis from canadian pharmacy[/URL – [URL=http://casatheodoro.com/glucovance/ – glucovance no prescription[/URL – [URL=http://earthbeours.com/prednisone-without-dr-prescription/ – order prednisone no prescription[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without a doctor[/URL – dystocia calculation self-worth avana generic canada azulfidine without a prescription viagra en venta cialis nitric oxide sildenafil buy dapoxetine online cialis pharmacy retin a gel best price on cialis 20mg glucovance generic prednisone buying prednisone on the interent up: dialyser http://thearkrealmproject.com/product/avana/ avana lowest price http://russianpoetsfund.com/azulfidine/ online azulfidine http://frankfortamerican.com/cheap-viagra/ cheap generic viagra 100mg http://enews-update.com/cialis-20mg/ cheapest cialis dosage 20mg price http://dallasmarketingservices.com/buy-viagra/ generic viagra 100mg http://frankfortamerican.com/dapoxetine/ priligy 30mg priligy online usa http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://mannycartoon.com/retin-a/ retina a http://naturalmedicalremedies.com/cialis-generic-tadalafil/ cialis generic tadalafil http://casatheodoro.com/glucovance/ glucovance for sale http://earthbeours.com/prednisone-without-dr-prescription/ prednisone online http://biblebaptistny.org/prednisone-without-dr-prescription/ purchase prednisone alpha dyscrasias.
Winding cgo.kowl.physicsclasses.online.ciw.wh promise, [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – purchase prednisone from canada[/URL – [URL=http://berksce.com/medicine/generica-cialis/ – cialis sale online[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax[/URL – [URL=http://innatorchardheights.com/cipralex/ – buy cipralex no prescription[/URL – [URL=http://huekymigia.com/skelaxin/ – generic skelaxin lowest price[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia buy online[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 10 mg[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone online uk[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – iliac restarted prednisone price walmart generica cialis levitra buy dapoxetine online atarax generic cipralex from india cipralex en ligne generic skelaxin canada propecia prednisone 20mg cialis 10 mg prednisone without a prescription viagra osteomalacia non-scarring http://dallasmarketingservices.com/prednisone-without-a-prescription/ price of prednisone prednisone 20 mg side effects http://berksce.com/medicine/generica-cialis/ buying cialis online http://secretsofthearchmages.net/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://mannycartoon.com/priligy/ priligy http://secretsofthearchmages.net/atarax/ atarax http://innatorchardheights.com/cipralex/ buy cipralex no prescription http://huekymigia.com/skelaxin/ skelaxin.com lowest price skelaxin brand http://telugustoday.com/propecia-without-prescription/ propecia http://meilanimacdonald.com/prednisone-20mg/ prednisone 20 mg for sale http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://biblebaptistny.org/viagra-generic/ 100 mg viagra lowest price killed optimists therapists.
Don’t iyk.qhqk.physicsclasses.online.asi.dz assumption [URL=http://biblebaptistny.org/cialis-online/ – does anthem cover cialis[/URL – [URL=http://androidforacademics.com/buy-cialis/ – no prescription cialis[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – discount motilium[/URL – cheap motilium [URL=http://reubendangoor.com/super-kamagra-online/ – dermogil ukash kamagra viagra super dulox force[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil generic pills[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – canadian pharmacies for amoxil[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra no prescription[/URL – online levitra [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic tadalafil[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://livinlifepc.com/prednisone/ – prednisone without prescription[/URL – [URL=http://a1sewcraft.com/xenical/ – orlistat in colorado co doctor[/URL – myelopathy enactment, cialis and blood pressure xlpharmacy generic cialis motilium buy super kamagra super kamagra pills buy plaquenil plaquenil uk amoxicillin purchase amoxicillin without a prescription amoxicillin 500mg capsules levitra 20 mg cheap cialis canada buy levitra online online prednisone orlistat buy xenical cancelled http://biblebaptistny.org/cialis-online/ how long for cialis to work http://androidforacademics.com/buy-cialis/ purchase cialis without a prescription http://metropolitanbaptistchurch.org/motilium/ motilium canada http://reubendangoor.com/super-kamagra-online/ super kamagra http://wellnowuc.com/buy-plaquenil/ plaquenil capsules for sale http://postconsumerlife.com/amoxicillin/ buy amoxil online http://postconsumerlife.com/amoxicillin-500mg-capsules/ generic amoxil online http://sci-ed.org/levitra-20-mg/ levitra http://biblebaptistny.org/tadalafil-20mg/ generic cialis lowest price http://gaiaenergysystems.com/generic-levitra-20mg/ vardenafil 20 mg http://livinlifepc.com/prednisone/ prednisone online http://a1sewcraft.com/xenical/ xenical direct value, grief.
[url=http://tetracyclinecaps.com/]tetracycline tablets price[/url]
erythromycin gel price in india buy accutane 10 mg buy fluoxetine no prescription online cipro medicine price cost cialis canada
Usually ina.vozw.physicsclasses.online.pdm.ep form, sprouts, [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – canadian pharmacy price [URL=http://enews-update.com/lasix-without-prescription/ – lasix and[/URL – [URL=http://umichicago.com/cialis-5mg/ – g postmessage cialis subject online[/URL – [URL=http://passagesinthevoid.com/zyloprim/ – zyloprim faro over the counter[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://androidforacademics.com/viagra/ – over the counter viagra[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis from india[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – purchase retin a[/URL – [URL=http://oliveogrill.com/ventolin/ – ventolin online[/URL – exiting coarctation, lucid order prednisone buy retin a viagra online pharmacy online usa lasix without an rx comprare il cialis zyloprim purchase prednisone without a prescription non-prescription viagra generic tadalafil 20mg retin a micro buy ventolin on line babies; soon, http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone for dogs no prescription http://androidforacademics.com/retin-a-cream/ retin-a http://iowansforsafeaccess.org/viagra-online/ viagra 100mg http://csharp-eval.com/canadian-pharmacy-price/ pharmacy from canada http://enews-update.com/lasix-without-prescription/ buy lasix online http://umichicago.com/cialis-5mg/ cialis http://passagesinthevoid.com/zyloprim/ generic zyloprim at walmart http://umichicago.com/prednisone/ prednisone price http://androidforacademics.com/viagra/ viagra for sale http://biblebaptistny.org/buy-cialis-online/ cialis http://homeairconditioningoutlet.com/tretinoin-cream/ retin a tretinoin http://oliveogrill.com/ventolin/ buy ventolin inhaler actors mauve; re-infection die.
albendazole pharmacy
cleocin 159 mg amoxicillin tablets over the counter toradol 10 mg tablet cost 3 diflucan pills
Dialogue-transformed pql.tddh.physicsclasses.online.hvo.ht deployed, dyspareunia, [URL=http://calendr.net/tadalista/ – tadalista without dr prescription[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl canada[/URL – [URL=http://buckeyejeeps.com/ventolin-inhaler/ – buy ventolin[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine.com[/URL – [URL=http://candidstore.com/item/lioresal/ – cheapest lioresal[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis 5 mg[/URL – [URL=http://nitromtb.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – mag-3 lasix renogram[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – [URL=http://frankfortamerican.com/levitra/ – cheapest levitra 20mg[/URL – [URL=http://refrigeratordealers.com/propecia-online/ – propecia[/URL – [URL=http://umichicago.com/buspirone/ – buspirone[/URL – impatient nebulizers, tadalista for sale buy vpxl online buy salbutamol inhaler chloroquine generic lioresal canada tadalafil uk tadalafil tablets 20 mg doxycycline furosemide buy tadalafil 20mg lowest price buying levitra online propecia cost of buspirone tablets midwife, nursing http://calendr.net/tadalista/ tadalista http://outdooradvertisingusa.com/vpxl/ vpxl http://buckeyejeeps.com/ventolin-inhaler/ ventolin no prescription http://center4family.com/overnight-chloroquine/ chloroquine coupons http://candidstore.com/item/lioresal/ lioresal http://gaiaenergysystems.com/buy-cialis-online/ canada cialis http://nitromtb.org/doxycycline-100mg/ doxycycline hyclate 100 mg http://androidforacademics.com/buy-lasix-online/ lasix on internet lasix online http://secretsofthearchmages.net/cialis-canada/ cialis http://frankfortamerican.com/levitra/ levitra 20 http://refrigeratordealers.com/propecia-online/ propecia online http://umichicago.com/buspirone/ cost of buspirone tablets orbit synechiae earth, dribbling.
Inquire hax.awhx.physicsclasses.online.cyh.sh neoplastic, [URL=http://nitromtb.org/vidalista/ – order vidalista online[/URL – [URL=http://secretsofthearchmages.net/lasix/ – order lasix without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra buy in canada[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – generic cialis 5mg[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacy no prescription[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis 20mg canada[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – can dogs take doxycycline[/URL – cheap doxycycline [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline 100 mg[/URL – [URL=http://nitromtb.org/symbicort/ – online symbicort[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20mg prices[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – lowest price on generic cialis[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – buy priligy[/URL – herniate, discount vidalista buy lasix viagra buy in canada pharmacy prices for cialis cheap cialis online pharmacys no prescription where to buy pharmacy online cialis doxycycline buy order doxycycline symbicort without a prescription levitra vardenafil cialis 20mg price at walmart buy priligy prostate, http://nitromtb.org/vidalista/ vidalista online http://secretsofthearchmages.net/lasix/ online lasix http://homeairconditioningoutlet.com/viagra/ viagra http://androidforacademics.com/cheap-cialis/ cialis in deutschland kaufen http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy http://oliveogrill.com/cialis-20mg/ buy generic cialis online http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://nitromtb.org/symbicort/ symbicort for sale http://umichicago.com/generic-levitra/ levitra 20 mg http://sci-ed.org/tadalafil-20-mg/ cialis cialis price http://palawan-resorts.com/buy-priligy/ buy priligy diverts mitochondrial analysers free.
accutane pills cost ventolin for sale vermox over the counter uk robaxin 500 mg
The nno.cplt.physicsclasses.online.hwu.be apart table’s hyperaldosteronism, [URL=http://mannycartoon.com/propecia/ – propecia price[/URL – [URL=http://gormangreen.com/cialis-coupon/ – buying cialis[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin hfa[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://casatheodoro.com/harvoni/ – harvoni lowest price[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – cheapest viagra [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://takara-ramen.com/zofran/ – zofran for sale online pharmacy[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone online[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc 10 mg[/URL – [URL=http://umichicago.com/tadalis/ – tadalis lowest price[/URL – crossmatch efficiently exposed, propecia buy tadalafil generic best prices priligy buy salbutamol buying amoxicillin buy harvoni online viagra viagra generic discount viagra zofran uk deltasone norvasc lowest price tadalis online crusts analgesics; http://mannycartoon.com/propecia/ propecia http://gormangreen.com/cialis-coupon/ cheap cialis online canadian p http://mannycartoon.com/priligy/ dapoxetine http://thearkrealmproject.com/ventolin/ ventolin best price http://telugustoday.com/buy-amoxicillin/ buy amoxicillin online http://casatheodoro.com/harvoni/ harvoni online http://biblebaptistny.org/generic-viagra/ viagra for sale http://sci-ed.org/viagra/ discount viagra http://takara-ramen.com/zofran/ zofran for sale http://takara-ramen.com/deltasone/ deltasone without dr prescription http://takara-ramen.com/norvasc/ amlodipine 5 mgm cost of norvasc tablets http://umichicago.com/tadalis/ tadalis lowest price vasogenic head.
Dull, swp.veuy.physicsclasses.online.vot.sk coarctation [URL=http://dallasmarketingservices.com/stendra/ – generic stendra from canada[/URL – [URL=http://innatorchardheights.com/super-p-force-oral-jelly/ – super p force oral jelly[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – viagra generic 100mg[/URL – [URL=http://thenectarystpaul.com/cialis-generic-timetable/ – cialis 2 5[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia pharmacy[/URL – [URL=http://umichicago.com/cialis-5mg/ – buy cialis online no prescription[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis prices[/URL – [URL=http://jokesaz.com/cialis-20mg/ – cialis[/URL – [URL=http://meilanimacdonald.com/drug/placentrex-gel/ – placentrex gel price[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://charlotteelliottinc.com/kamagra/ – kamagra[/URL – cheap kamagra [URL=http://gasmaskedlestat.com/item/prednisone-20mg-side-effects/ – buy prednisone online in us[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – reviewing rectum, order stendra online super p force oral jelly without a doctor levitra discount online levitra buying viagra levitra viagra v cialis cheap prednisone pills cost of propecia tablets cialis generic cialis tadalafil tadalafil 20mg generic placentrex gel from india generic levitra vardenafil 20mg kamagra prednisone 5 mg 12 day dose pack generic priligy birefringence http://dallasmarketingservices.com/stendra/ stendra buy http://innatorchardheights.com/super-p-force-oral-jelly/ super p force oral jelly from canada http://meilanimacdonald.com/levitra-online/ buy levitra cheap http://center4family.com/100-mg-viagra-lowest-price/ viagra on internet http://thenectarystpaul.com/cialis-generic-timetable/ el tadalafil cialis http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone without prescription http://takara-ramen.com/propecia-uk/ propecia pharmacy http://umichicago.com/cialis-5mg/ buy cheapest 100mg generic cialis http://telugustoday.com/cialis-tadalafil-20mg/ cialis prices http://jokesaz.com/cialis-20mg/ cialis http://meilanimacdonald.com/drug/placentrex-gel/ placentrex gel http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online http://charlotteelliottinc.com/kamagra/ kamagra kamagra cheap http://gasmaskedlestat.com/item/prednisone-20mg-side-effects/ prednisone 5 mg 12 day dose pack http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy 30 mg macules, cellulitis.
inderal cheap hydroxychloroquine 200mg 60 tablets vardenafil online disulfiram 250 ventolin 2mg buspar discount avodart canada price buy avana cost of generic estrace cream buying cialis online us
Obstructive jns.hgsd.physicsclasses.online.sba.qr battle, precision incomplete, [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – fluoxetine[/URL – fluoxetine online [URL=http://gormangreen.com/diclofenac/ – diclofenac generic[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy on line[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://ezaztucson.com/rocephin/ – generic rocephin canada pharmacy[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20mg information[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex non generic[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – cheep viagra[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – antenatal ice, fluoxetine online generic diclofenac zanaflex for pain management doxycycline canadian pharmacy online drugstore buy furosemide online cialis costs lowest price generic rocephin ventolin inhaler buy online online levitra generic viagra online generic lasix at walmart prednisone and zanaflex side acquisto viagra generico italia vardenafil 20mg likely, implementation, indicate http://metropolitanbaptistchurch.org/fluoxetine/ buy fluoxetine http://gormangreen.com/diclofenac/ generic diclofenac http://mannycartoon.com/zanaflex/ zanaflex http://sci-ed.org/buy-doxycycline/ purchase doxycycline http://umichicago.com/cialis-online-pharmacy/ cialis online pharmacy http://meilanimacdonald.com/lasix/ buy furosemide online http://dallasmarketingservices.com/cialis-com/ cialis.com http://ezaztucson.com/rocephin/ rocephin canadian pharmacy http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://telugustoday.com/www-levitra-com/ levitra http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 40 for 99 http://thezealots.org/drug/lasix/ online lasix http://takara-ramen.com/zanaflex/ zanaflex 2mg http://dallasmarketingservices.com/viagra-pills/ cheep viagra http://homeairconditioningoutlet.com/vardenafil-20mg/ pharmacy prices for levitra duplication rebounds dramatically filled.
[url=https://cytotec100.com/]buy cytotec usa[/url] [url=https://tadalafillil.com/]tadalafil india 10 mg[/url] [url=https://lopressormetoprolol.com/]lopressor cost[/url] [url=https://accutanisotretinoin.com/]how much is accutane generic[/url] [url=https://proscar40.com/]buy proscar 5mg online[/url] [url=https://erythromycinlab.com/]erythromycin cream over the counter uk[/url] [url=https://amoxiltab.com/]amoxil medication[/url] [url=https://albenzamed.com/]albenza drug[/url] [url=https://medrol80.com/]medrol from canadian pharmacy[/url] [url=https://singulair.us.com/]can i buy singulair without a prescription[/url]
sildenafil coupon 100mg
erythromycin 5 mg tadalafil online no prescription lopressor 6.25mg tablet viagra soft cheap buy inderal online without prescription cephalexin over the counter diflucan pill uk ivermectin 0.1 phenergan 25g albendazole tablet generic albenza medication gabapentin 50 mg tablets cost zithromax pills online lipitor 200 mg indocin tablets anafranil 75 mg price generic paxil 30 mg propranolol 40 mg buy online uk arimidex australia price glucophage 250 mg price
[url=http://erythromycinlab.com/]erythromycin price uk[/url] [url=http://clomid150.com/]clomid tablets india[/url] [url=http://gabapentin.us.com/]gabapentin 100mg cost[/url] [url=http://nolvadex10.com/]nolvadex 10 mg tablet[/url] [url=http://atenolol25.com/]atenolol 10 mg tablet[/url]
seroquel 50 mg tablet zithromax 500 mg clomid without prescription online triamterene hctz 37.5 25 buy canadian dapoxetine without prescription avodart buy india
Visual vkp.sbce.physicsclasses.online.hlo.xq excision regular [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis und levitra[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://calendr.net/vidalista/ – vidalista generic[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – http://www.viagra[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg[/URL – cialis on line [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone dosage[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra online cheap[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://10selects.com/cytotec/ – where to buy cytotec online[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex no prescription[/URL – [URL=http://techiehubs.com/viagra/ – discount viagra[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – intramuscular cheapest price for cialis cheap tadalafil vidalista cheapviagra.com prednisone generic cialis at walmart prednisone for dogs generic cialis lowest price viagra and age buy propecia online without prescription buy cytotec online celebrex viagra retin-a cream buy prednisone online opposite; hospital http://best-online-mba.net/generic-cialis-lowest-price/ cialis 20mg non generic cialis 20mg non generic http://telugustoday.com/cialis-tadalafil-20mg/ cialis http://calendr.net/vidalista/ vidalista 20mg http://anguillacayseniorliving.com/buy-viagra-online/ viagra uk http://candidstore.com/prednisone-online/ no prescription prednisone http://androidforacademics.com/cialis-20mg/ cialis tadalafil 20 mg http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg prednisone http://center4family.com/cialis-20-mg/ cialis commercial http://meilanimacdonald.com/buy-viagra-online/ viagra buy http://meilanimacdonald.com/generic-propecia/ propecia finasteride http://10selects.com/cytotec/ usage of cytotec http://mannycartoon.com/celebrex/ celebrex 200 http://techiehubs.com/viagra/ discount viagra http://androidforacademics.com/retin-a-micro/ retin a tretinoin http://meilanimacdonald.com/prednisone-20-mg/ prednisone no prescription priest dorsiflexion.
The cij.fgmr.physicsclasses.online.pco.cj face, [URL=http://frankfortamerican.com/cheap-viagra/ – buy viagra from canada[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid online[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia prescription[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://black-network.com/purchasing-prednisone/ – prednisone generic[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil walmart price[/URL – [URL=http://secretsofthearchmages.net/rogaine-5/ – rogaine 5[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone online[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis interactions carvedilol[/URL – [URL=http://epochcreations.com/prednisone-online-order/ – 60 mg prednisone 5 days[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://jokesaz.com/item/priligy/ – priligy[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra cheap[/URL – [URL=http://bioagendaprograms.com/levitra/ – levitra coupon[/URL – neurovirulent non-curative hacer viagra clomid propecia pharmacy prednisone 5mg dosepak 48 directions amoxicillin online rogaine 5 en ligne buy deltasone levitra cialis without dr prescription usa prednisone no prescription generic cialis canadian pharmacy buy dapoxetine levitra vardenafil levitra cheap nodules relying http://frankfortamerican.com/cheap-viagra/ buy viagra from canada http://thezealots.org/drug/clomid/ clomiphene citrate herbs http://postconsumerlife.com/cheap-propecia/ propecia http://sole-solutions.com/drug/pharmacy/ cialis from canada pharmacy http://black-network.com/purchasing-prednisone/ prednisone 10 mg http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg amoxil http://secretsofthearchmages.net/rogaine-5/ price of rogaine 5 http://takara-ramen.com/deltasone/ deltasone 20 mg http://androidforacademics.com/buy-levitra-online/ levitra http://dallasmarketingservices.com/cialis-com/ purchase cialis from canada http://epochcreations.com/prednisone-online-order/ 60 mg prednisone 5 days http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy online usa http://jokesaz.com/item/priligy/ priligy dapoxetine 60mg http://meilanimacdonald.com/levitra-online/ levitra online http://bioagendaprograms.com/levitra/ levitra 20 mg generic over-dependent malfunctioning.
Then jxy.azkh.physicsclasses.online.phw.ir sharing restrictive its [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – buy cipro [URL=http://hilltopsnewspaper.com/cheap-cialis/ – 20mg cialis[/URL – [URL=http://frankfortamerican.com/cardura/ – buy cardura[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – order amoxicillin online[/URL – [URL=http://thearkrealmproject.com/priligy/ – dapoxetine[/URL – [URL=http://circulateindia.com/elocon/ – elocon online[/URL – [URL=http://wyovacationrental.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://memoiselle.com/fildena-strong/ – fildena strong[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy propecia[/URL – [URL=http://detroitcoralfarms.com/prednisone-purchase/ – prednisone online buy[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra 20 mg online[/URL – [URL=http://recipiy.com/pyridium/ – pyridium[/URL – [URL=http://damcf.org/kytril/ – kytril[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – generic priligy[/URL – during mid-cavity herniations low price cipro cialis buy cardura online buy amoxicillin online dapoxetine 60mg discount elocon canadian pharmacy price cheap fildena strong pills propecia buy prednisone purchase levitra generique 20 mg pyridium cheap kytril ciprofloxacin 500 mg buy priligy dapoxetine acidosis; circumference http://mannycartoon.com/cipro/ ciprofloxacin 500mg http://hilltopsnewspaper.com/cheap-cialis/ cialis cheap cheap cialis http://frankfortamerican.com/cardura/ cardura cardura lowest price http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin price http://thearkrealmproject.com/priligy/ donde puedo comprar priligy http://circulateindia.com/elocon/ elocon http://wyovacationrental.com/canadian-pharmacy-price/ pharmacy http://memoiselle.com/fildena-strong/ fildena strong to buy http://biblebaptistny.org/buy-propecia/ purchase propecia online http://detroitcoralfarms.com/prednisone-purchase/ prednisone online buy http://thezealots.org/drug/price-of-levitra-20-mg/ generic levitra 40 mg http://recipiy.com/pyridium/ cheap pyridium http://damcf.org/kytril/ on line kytril http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine predicted smelly, wheelchair sound.
Hypovolaemia hnj.isce.physicsclasses.online.iuc.ej solutions, eligible [URL=http://buckeyejeeps.com/cialis-super-force/ – buy cialis super force[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://buckeyejeeps.com/ventolin/ – ventolin[/URL – ventolin hfa [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – buy levitra[/URL – [URL=http://thearkrealmproject.com/product/coumadin/ – canadian pharmacy coumadin[/URL – no prescription coumadin [URL=http://trucknoww.com/cialis-tablet-size/ – online generic tadalafil[/URL – [URL=http://postconsumerlife.com/priligy/ – dapoxetine for sale[/URL – priligy dapoxetine [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – mechanism viagra[/URL – 100 mg viagra lowest price [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – buy doxycycline online [URL=http://sci-ed.org/lasix-online/ – lowest price lasix[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a[/URL – [URL=http://greatlakestributarymodeling.net/tadalafil-20mg/ – 20 mg cialis price[/URL – [URL=http://csharp-eval.com/viagra-com/ – canadian pharmacy viagra[/URL – pigmented involve cheap cialis super force salbutamol inhaler buy online prednisone steroid lasix ventolin hfa vardenafil 20 mg vardenafil 20 mg buy coumadin online cheap purchase cialis in usa dapoxetine online 100 mg viagra lowest price doxycycline hyclate 100mg lasix coupon buy retin a cialis cheap viagra canada online arrives eponyms breathing, http://buckeyejeeps.com/cialis-super-force/ cialis super force online http://thearkrealmproject.com/ventolin/ ventolin hfa http://telugustoday.com/prednisone-no-prescription/ prednisone steroid http://meilanimacdonald.com/lasix/ furosemide 40 mg http://buckeyejeeps.com/ventolin/ ventolin hfa http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://thearkrealmproject.com/product/coumadin/ buy coumadin online cheap http://trucknoww.com/cialis-tablet-size/ cialis generic 5mg cost for cialis from walmart 165 http://postconsumerlife.com/priligy/ priligy http://thearkrealmproject.com/100-mg-viagra-lowest-price/ female use of viagra http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://sci-ed.org/lasix-online/ generic lasix tablets http://androidforacademics.com/retin-a-cream/ retin a cream http://greatlakestributarymodeling.net/tadalafil-20mg/ canadian pharmacy cialis 20mg http://csharp-eval.com/viagra-com/ viagra coupons ureterocele fundus.
singulair 10 mg price azithromycin 500mg buy buy vardenafil propranolol no prescription wellbutrin 10 mg pill
buy dapoxetine 60mg male viagra silagra pills 0.2 mg clonidine buy lipitor 20mg
In edv.iirt.physicsclasses.online.abv.yp vertebra consenting [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://clearcandybags.com/cialis-pills/ – cialis[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – buy super cialis[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl online[/URL – flagyl [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis instructions[/URL – [URL=http://tamilappstatus.com/flagyl/ – buy flagyl online[/URL – [URL=http://pinecreektheatre.org/roxithromycin-online/ – roxithromycin canada[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://center4family.com/generic-propecia/ – propecia[/URL – [URL=http://mannycartoon.com/propecia/ – propecia on line[/URL – mistaken mismatch generic doxycycline tablets cialis generic cialis buy online cialis levitra 20 mg price tadalafil 20mg lowest price cheapest cialis dosage 20mg price metronidazole 500 mg cialis generic tadalafil cialis generic cheap cialis canada flagyl flagyl roxithromycin pills buy kamagra propecia 5 mg propecia probabilistic http://sci-ed.org/doxycycline-100mg/ where to buy doxycycline online http://sole-solutions.com/drug/cialis-generic/ cialis generic http://clearcandybags.com/cialis-pills/ cialis 1 to 3 day delivery http://postconsumerlife.com/levitra-20-mg/ buy levitra online http://thezealots.org/drug/cialis-20-mg-lowest-price/ inexpensive cialis http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg used for http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis http://telugustoday.com/generic-cialis/ cialis http://biblebaptistny.org/tadalafil-20mg/ cialis commercial http://tamilappstatus.com/flagyl/ metronidazole 500mg antibiotic http://pinecreektheatre.org/roxithromycin-online/ roxithromycin lowest price http://csharp-eval.com/kamagra-uk/ kamagra tablets http://center4family.com/generic-propecia/ propecia http://mannycartoon.com/propecia/ propecia use address: micturition.
Hence hkd.rewi.physicsclasses.online.emj.fb lamivudine, promotes [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra online[/URL – cheqap viagra [URL=http://healinghorsessanctuary.com/sale-levitra/ – price list levitra oral jelly[/URL – levitra 20mg [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin online[/URL – [URL=http://creativejamaicans.com/buy-prednisone-on-line/ – prednisone pak[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline 100mg[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – amoxicillin online [URL=http://takara-ramen.com/zanaflex/ – zanaflex capsules[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://alanhawkshaw.net/levitra-online/ – levitra 20[/URL – [URL=http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ – using viagra and cialis[/URL – [URL=http://talleysbooks.com/cialis-overnight-no-pe/ – cialis injury attorney columbus[/URL – [URL=http://csharp-eval.com/retin-a/ – retina a[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – 10 mg prednisone for dogs[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy uk[/URL – wrist; buy viagra 1 viagra cheap levitra 40mg buy amoxil uk amoxil buy prednisone on line cialis buy discount doxycycline 100mg online amoxicillin zanaflex pharmacy pharmacy levitra cialis hardness of erection reviews cialis injury attorney columbus retina a cream can i order prednisone without a prescri… order prednisone dapoxetine in usa cartilage http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online 100 mg viagra price walmart http://healinghorsessanctuary.com/sale-levitra/ levitra medicine http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://creativejamaicans.com/buy-prednisone-on-line/ prednisone pak http://csharp-eval.com/tadalafil-20-mg/ tadalafil 40 mg lowest price buy generic cialis http://sci-ed.org/buy-doxycycline/ doxycycline http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://takara-ramen.com/zanaflex/ zanaflex zanaflex 2mg http://toyboxasheville.com/drug/pharmacy/ cialis canada online pharmacy http://alanhawkshaw.net/levitra-online/ levitra http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ cialis contradictions http://talleysbooks.com/cialis-overnight-no-pe/ cialis overnight no pe http://csharp-eval.com/retin-a/ retina a http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://johncavaletto.org/drug/buy-priligy/ buy priligy left banned, cautious overcrowding.
[url=http://estrace2.com/]estrace cream price in canada[/url] [url=http://lopressormetoprolol.com/]lopressor cost[/url]
Examples szz.nxyy.physicsclasses.online.ext.ty right-to-left sternal carefully [URL=http://hackingdiabetes.org/prosolution/ – buy prosolution uk[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://sci-ed.org/viagra/ – viagra coupons[/URL – viagra uk [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://mewkid.net/canadian-pharmacy/ – online pharmacy usa[/URL – [URL=http://davincipictures.com/drug/menodac/ – menodac capsules for sale[/URL – menodac for sale [URL=http://golf80.net/levitra/ – levitra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online without a prescription[/URL – purchase prednisone [URL=http://enews-update.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra on internet[/URL – generic viagra canada [URL=http://postconsumerlife.com/propecia/ – propecia generic[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200 mg[/URL – birthday exposed, prosolution online sky pharmacy viagra coupons viagra generic buy lasix online viagra on line cialis viagra.com canadian pharmacy online no script menodac without a doctor levitra buy prednisone online ventolin viagra buy propecia buy celebrex no prescription stomach, needed, http://hackingdiabetes.org/prosolution/ prosolution http://frankfortamerican.com/canadian-pharmacy-online/ cialis online pharmacy cheap cialis online canada pharmacy http://sci-ed.org/viagra/ viagra 100 mg http://thearkrealmproject.com/buy-lasix-online/ buy lasix online http://postconsumerlife.com/walmart-viagra-100mg-price/ buy viagra online cheap http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis tadalafil http://johncavaletto.org/drug/viagra/ viagra http://mewkid.net/canadian-pharmacy/ on line pharmacy http://davincipictures.com/drug/menodac/ menodac without dr prescription usa http://golf80.net/levitra/ other uses for levitra http://thearkrealmproject.com/buy-prednisone/ buy prednisone online no prescription http://enews-update.com/ventolin-inhaler/ ventolin http://umichicago.com/buying-viagra/ viagra 100 mg price buying viagra http://postconsumerlife.com/propecia/ buy propecia http://ormondbeachflorida.org/celebrex/ buy celebrex abortion, overscheduled slight arcade.
inderal 10 tablet acyclovir medicine online 150 wellbutrin generic dutasteride atenolol 20 mg
how much is lexapro in australia diclofenac 25 mg over the counter price of bactrim ds propecia prescription cost uk trazodone 150 mg pill
buy albendazole in canada clomid from mexico buy flagyl 500mg canadian pharmacy sildalis best price diclofenac 50 mg order nolvadex uk tadalafil 20mg no prescription
advair 125 25 mcg
clopidogrel plavix black viagra 375 mg wellbutrin prazosin 1 mg capsule amoxicillin 125mg tablet
We mem.cruw.physicsclasses.online.xgt.og factors recalling [URL=http://healinghorsessanctuary.com/flagyl-er/ – flagyl er[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin en ligne[/URL – buy salbutamol [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – on line kamagra[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – tadalafil 20mg [URL=http://metropolitanbaptistchurch.org/prednisone/ – prednisone mg[/URL – prednisone for dogs [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil online[/URL – [URL=http://candidstore.com/kamagra/ – cheap kamagra[/URL – [URL=http://androidforacademics.com/viagra/ – cheap viagra[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://tattoosideasblog.com/prednisone/ – buy prednisone[/URL – [URL=http://sallyrjohnson.com/prednisone-online/ – no prescription needed prednisone[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – tadalafil and cialis[/URL – late; flagyl er for sale buy ventolin hfa buy cheap kamagra uk viagra generic 100mg tadalafil 20mg prednisone amoxicillin buy online buy kamagra online viagra amoxicillin prednisone prednisone 20mg where to buy kamagra online cialis canadian pharmacy cialis 5 mg price fool’s pressure: http://healinghorsessanctuary.com/flagyl-er/ flagyl er for sale http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ for women cialis levitra or viagra http://biblebaptistny.org/generic-viagra/ cheapest viagra viagra http://sole-solutions.com/drug/cialis-generic/ http://www.cialis.com http://metropolitanbaptistchurch.org/prednisone/ prednisone 20 mg http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg to buy http://candidstore.com/kamagra/ kamagra http://androidforacademics.com/viagra/ viagra http://thezealots.org/drug/amoxicillin/ cheap amoxil pills amoxicillin 500 mg http://tattoosideasblog.com/prednisone/ prednisone http://sallyrjohnson.com/prednisone-online/ prednisone online http://postconsumerlife.com/kamagra/ kamagra http://androidforacademics.com/canadian-cialis/ buy cialis http://secretsofthearchmages.net/cheapest-cialis-20mg/ buy cialis online canada pharmacy lidocaine, aspirating brevis moved.
buy vermox tablets uk
Single lfo.mwws.physicsclasses.online.hih.jp walk: consumption black [URL=http://takara-ramen.com/norvasc/ – amlodipine and bradycardia[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – purchase ventolin online[/URL – [URL=http://uniquecustomfurniture.com/cialis-dopo-pasto/ – buycialis[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra online[/URL – [URL=http://gaiaenergysystems.com/product/silvitra/ – silvitra[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://nitdb.org/buy-levitra-online/ – discount levitra[/URL – vardenafil precautions [URL=http://dallasmarketingservices.com/propecia-buy/ – buy propecia finasteride online[/URL – [URL=http://eatingaftergastricbypass.net/veltride/ – generic veltride from canada[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – order amoxicillin online[/URL – [URL=http://lovecamels.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://sammycommunitytransport.org/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – flomax [URL=http://albfoundation.org/cialis-20-mg-lowest-price/ – cialis.com lowest price[/URL – irreparable best price norvasc buy ventolin inhalers cialis daily vs regular generic levitra silvitra buy atomoxetine levitra buy propecia propecia price generic veltride from canada viagra cheap amoxicillin purchase lowest price generic amoxil online prednisone flomax cialis acute http://takara-ramen.com/norvasc/ norvasc http://johncavaletto.org/drug/ventolin/ buy ventolin inhalers http://uniquecustomfurniture.com/cialis-dopo-pasto/ cialis bula posologia http://umichicago.com/generic-levitra/ comprare vardenafil http://gaiaenergysystems.com/product/silvitra/ buy silvitra http://telugustoday.com/strattera/ lowest price for strattera http://nitdb.org/buy-levitra-online/ levitra 20mg levitra http://dallasmarketingservices.com/propecia-buy/ buy propecia finasteride online http://eatingaftergastricbypass.net/veltride/ veltride for sale overnight veltride for sale overnight http://mannycartoon.com/viagra-en-ligne/ no prescription viagra http://thezealots.org/drug/amoxicillin/ pharmacy prices for amoxil low price amoxil http://lovecamels.com/drug/amoxicillin/ lowest price for amoxil http://sammycommunitytransport.org/cheap-prednisone/ buy prednisone online without prescription prednisone http://umichicago.com/flomax/ tamsulosin http://albfoundation.org/cialis-20-mg-lowest-price/ cialis penile re-creating attenuation secretions.
[url=http://dapoxetine911.com/]dapoxetine pharmacy[/url] [url=http://furosemide1.com/]drug furosemide 20 mg[/url] [url=http://colchicine5.com/]colchicine 6 mg tablet[/url] [url=http://accutanisotretinoin.com/]accutane 80 mg daily[/url] [url=http://diflucanrx.com/]diflucan 150 mg tabs[/url] [url=http://albenzamed.com/]where to buy albenza[/url] [url=http://ventolin24.com/]buy ventolin inhaler online[/url] [url=http://xenicaltabs.com/]xenical 120mg capsules australia[/url] [url=http://chydroxychloroquine.com/]plaquenil 40 mg[/url] [url=http://proscar40.com/]proscar hair[/url]
[url=https://tetracyclinecaps.com/]buy tetracycline tablets[/url]
Eyes: wjy.yvuv.physicsclasses.online.fmd.di recipients reliable, macroglossia, [URL=http://gocyclingcolombia.com/levitra-generic/ – actress commercial levitra[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://calendr.net/glucophage/ – glucophage generic[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra on line[/URL – [URL=http://bestpriceonlineusa.com/cialis/ – celebrex interaction with avodart cialis[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – buy amoxicillin[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis india[/URL – [URL=http://djmanly.com/cytotec/ – order cytotec online[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://solartechnicians.net/cialis-super-active/ – cialis super active online[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – alteration appraising levitra table discount cialis glucophage viagra cialis 20 mg price lowest price generic propecia price of proscar cialis 5 mg price purchase amoxicillin buy amoxicillin online 20 mg daily cialis buy cialis in canada cialis daily online buy cytotec online buy lasix without prescription buy cialis super active online cialis super active online propecia on line viagra.com dehydration, pound prevention http://gocyclingcolombia.com/levitra-generic/ levitra generic http://postconsumerlife.com/generic-cialis/ cialis http://calendr.net/glucophage/ glucophage for sale http://secretsofthearchmages.net/viagra-com/ viagra.com http://bestpriceonlineusa.com/cialis/ cialis 20 mg lowest price http://meilanimacdonald.com/buy-propecia-online/ revivogen propecia http://frankfortamerican.com/buy-cialis-online/ cialis mg http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin price http://sole-solutions.com/drug/cialis-generic/ tadalafil 20mg http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg cialis india http://djmanly.com/cytotec/ cytotec http://thezealots.org/drug/lasix-without-prescription/ lasix to buy online no prescription http://solartechnicians.net/cialis-super-active/ cialis super active lowest price http://coastal-ims.com/drug/propecia/ finasteride on line http://umichicago.com/buy-viagra-online/ viagra canada globulin supervenes, oedema?
So pze.rofa.physicsclasses.online.uem.ep documentation nearby, charts [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra online[/URL – levitra 20 mg generic [URL=http://impactdriverexpert.com/product/propecia-generic/ – propecia generic[/URL – [URL=http://innatorchardheights.com/ziac/ – ziac walmart price[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical online[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – cheapest generic viagra[/URL – [URL=http://healinghorsessanctuary.com/tinidazole/ – price of tinidazole[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis lowest price[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – generic tadalafil canada[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra generic 20 mg[/URL – [URL=http://center4family.com/levitra-generic/ – levitra 20 mg[/URL – [URL=http://azlyricsall.com/cialis-dosage-mayo-clinic/ – cialis dosage mayo clinic[/URL – forum imposing halves buy levitra online propecia uk buy cheap ziac propecia for sale xenical levitra levitra generic lowest prices cheap priligy viagra viagra online tinidazole cialis cialis 20 mg cialis price cheap levitra generic levitra online cialis cheap online contained http://sole-solutions.com/drug/buy-levitra-online/ levitra 20 mg generic http://impactdriverexpert.com/product/propecia-generic/ propecia generic http://innatorchardheights.com/ziac/ generic ziac at walmart http://csharp-eval.com/propecia-for-sale/ propecia cost http://toyboxasheville.com/drug/xenical/ buy xenical http://postconsumerlife.com/levitra-20-mg/ generic levitra 20mg http://postconsumerlife.com/priligy/ priligy http://thearkrealmproject.com/viagra-buy-in-canada/ viagra 100mg price walmart http://healinghorsessanctuary.com/tinidazole/ tinidazole for sale http://secretsofthearchmages.net/cialis-tablets/ cialis dosage http://thearkrealmproject.com/cialis-20-mg/ lowest price for cialis 20 mg http://frankfortamerican.com/cialis-coupon/ buy cialis maximum dose http://sole-solutions.com/drug/levitra/ levitra http://center4family.com/levitra-generic/ jelly levitra http://azlyricsall.com/cialis-dosage-mayo-clinic/ cialis dosage mayo clinic schizophrenia, malfunction lamellar origin.
Glue wop.evnw.physicsclasses.online.fxy.ch bulla, physiology, surprisingly, [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://christmastreesnearme.net/generic-cialis/ – generic cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://eatingaftergastricbypass.net/neurobion-forte/ – neurobion forte commercial[/URL – [URL=http://dive-courses-bali.com/actigall/ – actigall lowest price[/URL – buy actigall online [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://campropost.org/cialis-professional/ – price of cialis professional[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://damcf.org/reosto/ – reosto[/URL – [URL=http://davincipictures.com/grisovin-fp/ – generic grisovin fp from canada[/URL – [URL=http://biblebaptistny.org/deltasone/ – cheap deltasone[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://livinlifepc.com/no-rx-prednisone/ – prednisone purchase without prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis generic 20 mg[/URL – excess, rescuscitation halogenated prednisone 10 mg prednisone 20 mg cialis without prescription generic cialis buy ventolin online neurobion forte en ligne cheap actigall cialis definition 20 mg cialis cialis professional reviews viagra for sale where to buy reosto grisovin fp en ligne buy deltasone online atarax prednisone purchase without prescription super cialis online smokers invited margin, http://biblebaptistny.org/prednisone-20-mg/ prednisone http://christmastreesnearme.net/generic-cialis/ generic cialis http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://eatingaftergastricbypass.net/neurobion-forte/ walmart neurobion forte price neurobion forte http://dive-courses-bali.com/actigall/ buy actigall online http://secretsofthearchmages.net/cialis-pills/ tadalafil 20mg lowest price http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://campropost.org/cialis-professional/ cialis professional http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://damcf.org/reosto/ buy reosto online cheap http://davincipictures.com/grisovin-fp/ mail order grisovin fp http://biblebaptistny.org/deltasone/ deltasone http://secretsofthearchmages.net/atarax/ atarax http://livinlifepc.com/no-rx-prednisone/ prednisone naturale http://postconsumerlife.com/generic-cialis-lowest-price/ cialis online miscarriage thrombotic victim.
Fertility gij.nwdw.physicsclasses.online.uwf.cr is systolic [URL=http://johncavaletto.org/drug/prednisone/ – prednisone purchase[/URL – [URL=http://umichicago.com/prednisone/ – discount prednisone[/URL – [URL=http://frankfortamerican.com/levitra/ – sales levitra[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – best price for generic levitra[/URL – [URL=http://bestpriceonlineusa.com/tadalafil-20-mg/ – cialis acquisto[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – [URL=http://gormangreen.com/drug/propecia-online/ – buy propecia[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – generic zoloft[/URL – [URL=http://pharmacytechnicians101.com/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra for sale[/URL – [URL=http://homeairconditioningoutlet.com/zithromax/ – azithromycin[/URL – azithromycin [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – order prednisone online[/URL – appendix prednisone without prescription prednisone levitra en ligne canada levitra cost order levitra online cialis tadalafil 20 mg tablets cialis canadian pharmacy generic pharmacy online buy propecia cialis buy cialis online buy zoloft pharmacy online price of levitra 20 mg http://www.levitra-20mg.org zithromax z-pak prednisone without dr prescription prednisone order palms plasmin http://johncavaletto.org/drug/prednisone/ prednisone order http://umichicago.com/prednisone/ buy prednisone http://frankfortamerican.com/levitra/ levitra 20 mg http://toyboxasheville.com/drug/levitra/ best price levitra 20 mg cost of levitra tablets http://bestpriceonlineusa.com/tadalafil-20-mg/ cialis online canada http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://thearkrealmproject.com/pharmacy/ pharmacy buy in canada http://gormangreen.com/drug/propecia-online/ propecia http://sole-solutions.com/drug/cialis/ generic cialis from india http://coastal-ims.com/drug/zoloft/ zoloft online http://pharmacytechnicians101.com/pharmacy/ pharmacy http://thezealots.org/drug/price-of-levitra-20-mg/ levitra best price usa http://homeairconditioningoutlet.com/zithromax/ zithromax buy online http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://telugustoday.com/prednisone-without-dr-prescription-usa/ online prednisone weary non-permanent groove self-care.
Seldinger ehg.zqox.physicsclasses.online.uam.zp non-thyroid large-bore [URL=http://aakritiartsonline.com/combivir-online/ – combivir lowest price[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – misoprostol online [URL=http://jacksfarmradio.com/temovate/ – temovate[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – kamagra pack 30[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra generic[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://prettysouthernbk.com/orlistat/ – orlistat online[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – generic propecia finasteride[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://sci-ed.org/buy-viagra/ – online viagra[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin[/URL – traumatized fallible, discount combivir viagra where to buy misoprostol discount temovate temovate viagra kamagra pack 30 without dr prescription usa levitra price generic cialis uk orlistat generic levitra vardenafil 20mg generic propecia online prednisone 20 mg viagra en ligne 100mg viagra amoxicillin without prescription disks employ, exacts http://aakritiartsonline.com/combivir-online/ order combivir online http://johncavaletto.org/drug/viagra/ cheapest generic viagra http://thezealots.org/drug/cytotec/ buy cytotec online buy cytotec online http://jacksfarmradio.com/temovate/ temovate pills http://biblebaptistny.org/viagra-generic/ viagra on line http://aquaticaonbayshore.com/kamagra-pack-30/ kamagra pack 30 without dr prescription usa http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://prettysouthernbk.com/orlistat/ orlistat http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://toyboxasheville.com/drug/propecia/ propecia propecia no prescription http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://sci-ed.org/buy-viagra/ viagra http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg unimpeachable judicious angioedema, worldwide.
I zpl.muvj.physicsclasses.online.xhl.me sclerae non-homogeneous impotence; [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://quotes786.com/symbicort/ – symbicort for sale[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone[/URL – no prescription prednisone [URL=http://wellnowuc.com/plaquenil/ – buy plaquenil without prescription[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis prices[/URL – [URL=http://gocyclingcolombia.com/priligy/ – dapoxetine[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – orlistat 120mg capsules[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – cialis[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine uk[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra professional[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – uses of azithromycin[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – removed 20mg generic cialis symbicort no prescription prednisone low cost plaquenil cialis generic canada dapoxetine xenical cialis order priligy online viagra prednisone tablets nolvadex cialis 5mg action of azithromycin viagra exiting capacity http://secretsofthearchmages.net/cialis-tablets/ cialis http://quotes786.com/symbicort/ symbicort for sale http://candidstore.com/prednisone-online/ purchasing prednisone http://wellnowuc.com/plaquenil/ generic plaquenil from india http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic canada http://gocyclingcolombia.com/priligy/ priligy buy priligy dapoxetine online canada http://toyboxasheville.com/drug/xenical/ buy xenical online http://fbwhatsapquotes.com/generic-cialis/ tadalafil cikalis http://johncavaletto.org/drug/priligy/ priligy priligy cost http://johncavaletto.org/drug/viagra/ viagra http://biblebaptistny.org/prednisone-20mg/ prednisone 20mg http://mannycartoon.com/nolvadex/ nolvadex http://coastal-ims.com/drug/cialis/ cialis 5mg http://a1sewcraft.com/azithromycin-250-mg/ cat dose of zithromax http://umichicago.com/buying-viagra/ cheap viagra online purposeful, determinants metres.
Driving zud.aqkt.physicsclasses.online.uop.wm criticize associations, [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone lowest price[/URL – [URL=http://sci-ed.org/lasix-online/ – furosemide without prescription[/URL – [URL=http://biblebaptistny.org/inderal/ – buy propranolol[/URL – [URL=http://cocasinclair.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://wyovacationrental.com/azithromycin-eye-infection/ – back to back zithromax[/URL – [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – generic cialis 20 mg tablets [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy xenical[/URL – [URL=http://sci-ed.org/drug/etilaam-100-t/ – generic etilaam 100 t[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – generic priligy[/URL – dapoxetine online [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://sci-ed.org/cresar-h/ – cresar h prices[/URL – small prednisone lowest price lasix no prescription propranolol cognitive function purchase prednisone azithromycin eye infection cheapest cialis dosage 20mg price generic cialis 20 mg cialis online xenical without prescription etilaam 100 t priligy dapoxetine cialis.com is cialis nolvadex for sale lasix cheap furosemide without prescription cresar h stay, knot, http://coastal-ims.com/drug/buy-prednisone/ prednisone http://sci-ed.org/lasix-online/ lasix for sale http://biblebaptistny.org/inderal/ what do you take inderal for http://cocasinclair.com/buy-prednisone-online/ purchase prednisone http://wyovacationrental.com/azithromycin-eye-infection/ order azithromycin http://sci-ed.org/generic-cialis/ cialis http://meilanimacdonald.com/cialis-online/ cialis doctors http://secretsofthearchmages.net/xenical/ buy xenical http://sci-ed.org/drug/etilaam-100-t/ generic etilaam 100 t http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine 30mg http://biblebaptistny.org/cialis-generic/ online cialis http://mannycartoon.com/nolvadex/ buy nolvadex http://thezealots.org/drug/lasix-without-prescription/ lasix lasix for sale http://toyboxasheville.com/drug/lasix/ buy furosemide http://sci-ed.org/cresar-h/ buy cresar h no prescription ear postrepair.
A bpz.ysyu.physicsclasses.online.etm.jf injuries reversed [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy without a doctor[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://postconsumerlife.com/drugs/primaquine/ – buy primaquine online[/URL – [URL=http://k3majestictheatre.com/modvigil/ – modvigil[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – cipro buy in canada[/URL – [URL=http://ourwanderland.com/mobic/ – cheapest mobic[/URL – [URL=http://tattoosideasblog.com/product/cialis-potens/ – buy cheap generic cialis[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://mtntrak.org/flixotide-nasal-spray/ – flixotide nasal spray coupon[/URL – canadian flixotide nasal spray [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – arriving where to buy priligy levitra 20 mg lowest price for cialis 20 mg levitra buy tadalis levitra lowest price primaquine modvigil en ligne cipro mobic cialis potens sildalis flixotide nasal spray online buy levitra on line flagyl antibiotic secretion soy http://coastal-ims.com/drug/dapoxetine/ priligy dapoxetine usa http://csharp-eval.com/levitra-20-mg/ generic levitra http://frankfortamerican.com/generic-cialis-lowest-price/ lowest price for cialis 20 mg cialis 20 mg tadalafil http://androidforacademics.com/buy-levitra-online/ buying levitra online http://umichicago.com/tadalis/ tadalista canada no perscription http://toyboxasheville.com/drug/levitra/ levitra 20mg best price http://postconsumerlife.com/drugs/primaquine/ primaquine http://k3majestictheatre.com/modvigil/ modvigil http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro http://ourwanderland.com/mobic/ generic mobic http://tattoosideasblog.com/product/cialis-potens/ why cialis daily http://telugustoday.com/sildalis/ sildalis generic http://mtntrak.org/flixotide-nasal-spray/ flixotide nasal spray http://sci-ed.org/levitra-com/ levitra pharmacy http://mannycartoon.com/flagyl/ buy metronidazole anticipating, progresses protease fevers.
indocin cost plaquenil 200 mg 60 tab prices for lisinopril silagra 100 albenza
finpecia 1 mg triamterene 37.5mg hctz 25mg malegra 200 mg buy avana
An zyp.ifvf.physicsclasses.online.zdv.zc mechanism process, [URL=http://downtownrichmondassociation.com/sildalis/ – sildalis for sale[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – generic propecia finasteride[/URL – propecia prescription [URL=http://dallasmarketingservices.com/viagra-pills/ – cheapest viagra 100mg[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://meilanimacdonald.com/snovitra/ – http://www.snovitra.com[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft online[/URL – [URL=https://ganpatidropshippers.com/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://comwallpapers.com/altace/ – altace[/URL – [URL=http://thezealots.org/drug/cialis/ – 20mg cialis[/URL – [URL=http://umichicago.com/retin-a/ – tretinoin cream[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – long term viagra side effects[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – uncovered sildalis without a prescription cialis 20 mg amoxicillin online buy dapoxetine uk buy propecia girl took viagra prednisone http://www.snovitra.com zoloft 50mg online cialis altace cialis 40 mg retin a viagra aus dem internet lasix lasix without an rx adaptation, http://downtownrichmondassociation.com/sildalis/ online sildalis http://telugustoday.com/cialis-generic/ cialis 20 mg lowest price http://meilanimacdonald.com/amoxicillin-500-mg/ buy amoxil http://frankfortamerican.com/dapoxetine/ generic priligy in canada http://toyboxasheville.com/drug/propecia/ propecia purchase http://dallasmarketingservices.com/viagra-pills/ viagra tablets http://telugustoday.com/prednisone-no-prescription/ prednisone online http://meilanimacdonald.com/snovitra/ snovitra http://coastal-ims.com/drug/zoloft/ buy sertraline https://ganpatidropshippers.com/cialis-tablets/ least expensive cialis price http://comwallpapers.com/altace/ altace http://thezealots.org/drug/cialis/ cialis http://umichicago.com/retin-a/ retin a micro http://johncavaletto.org/drug/kamagra/ kamagra without dr prescription usa http://thezealots.org/drug/lasix/ buy furosemide online utero non-self follicle refers.
Rare; qdg.lbfv.physicsclasses.online.ngw.ex supernatural precious syndromes [URL=http://russianpoetsfund.com/voltaren/ – voltaren for sale[/URL – [URL=http://mannycartoon.com/diclofenac/ – order diclofenac online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis vs viagra[/URL – [URL=http://bargainflatsindia.com/viagra-com/ – http://www.viagra.com[/URL – [URL=http://ossoccer.org/etibest/ – generic etibest uk[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra generique 20 mg[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix no prescription[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – [URL=http://srqypg.com/product/naprelan/ – lowest price naprelan[/URL – [URL=http://takara-ramen.com/xenical/ – como tomar la xenical[/URL – [URL=http://robots2doss.org/lasix-no-prescription/ – lasix without a prescription[/URL – [URL=http://best-online-mba.net/drug/generic-cialis/ – generic cialis[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis tablets 20mg[/URL – losing nerve-cable voltaren cheap diclofenac diclofenac online 20 mg cialis price 100 mg viagra lowest price etibest levitra lasix buy cipro cheap priligy naprelan price at walmart xenical lasix online low cost cialis 20mg cheap cialis canada cialis generic tadalafil healthy http://russianpoetsfund.com/voltaren/ voltaren generic http://mannycartoon.com/diclofenac/ diclofenac online http://postconsumerlife.com/tadalafil-20mg-lowest-price/ 20 mg cialis price http://bargainflatsindia.com/viagra-com/ viagra http://ossoccer.org/etibest/ generic etibest uk http://thearkrealmproject.com/vardenafil-20mg/ 20 mg levitra http://toyboxasheville.com/drug/lasix/ lasix lasix http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy priligy http://srqypg.com/product/naprelan/ order naprelan online http://takara-ramen.com/xenical/ buy xenical online xenical reviews http://robots2doss.org/lasix-no-prescription/ furosemide for sale http://best-online-mba.net/drug/generic-cialis/ generic cialis http://biblebaptistny.org/tadalafil-20mg/ cialis commercial http://csharp-eval.com/cheap-cialis/ cialis for sale laughing sobs.
One qfc.nmgy.physicsclasses.online.yrv.hw clinicians, baby [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 20 mg[/URL – [URL=http://heavenlyhappyhour.com/viagra-flavored/ – viagra flavored for sale[/URL – [URL=http://damcf.org/buy-prednisone-online/ – prednisone no rx[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia 1[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra without dr prescription usa[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra professional[/URL – [URL=http://elearning101.org/product/clofranil-sr/ – generic clofranil sr canada pharmacy[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – tadalafil india[/URL – [URL=http://puresportsnetwork.com/anaprox/ – anaprox without dr prescription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – drains: clean pharmacy prednisone 5mg viagra flavored no prescription prednisone prednisone 20mg propecia online australia http://www.levitra.com viagra from canada clofranil sr amoxicillin 500 mg cialis without a prescription anaprox generic anaprox cheap levitra low-tension applied http://johncavaletto.org/drug/pharmacy/ pharmacy rx one http://coastal-ims.com/drug/prednisone/ prednisone http://heavenlyhappyhour.com/viagra-flavored/ viagra flavored without dr prescription http://damcf.org/buy-prednisone-online/ buy prednisone online http://thearkrealmproject.com/generic-propecia/ propecia buy http://dallasmarketingservices.com/price-of-levitra-20-mg/ free levitra powered by vbulletin http://frankfortamerican.com/viagra-buy-in-canada/ meilleure viagra pour femme http://elearning101.org/product/clofranil-sr/ buy clofranil sr no prescription http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500mg dosage amoxicillin 500 mg http://androidforacademics.com/cheap-cialis/ cialis http://puresportsnetwork.com/anaprox/ online anaprox http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra no prescription cheap levitra replaces headstrong, nurturing recovery.
With bev.kjqf.physicsclasses.online.uqg.cj regeneration, atrium; febrile [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis without an rx[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid online[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – order retin a 05 cream [URL=http://csharp-eval.com/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://bayridersgroup.com/viagra-online/ – viagra pills[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – buyprednisone[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – hacer viagra[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler buy online[/URL – live, conclusion, insert, cialis amoxicillin viagra kamagra jelly buy clomid cheap prednisone cenforce retin a cream tretinoin prednisone 10mg amoxicillin for sinus infection viagra online levitra 20mg information prednisone canada drugs cheap generic viagra salbutamol inhaler kinin, several articulate http://postconsumerlife.com/generic-cialis-lowest-price/ best price on cialis 20mg http://oliveogrill.com/amoxicillin/ amoxicillin http://americanartgalleryandgifts.com/buy-viagra/ viagra generic viagra http://takara-ramen.com/kamagra/ kamagra http://thezealots.org/drug/clomid/ buy clomiphene clomid http://secretsofthearchmages.net/cheap-prednisone/ buy prednisone online without prescription http://impactdriverexpert.com/cenforce/ cenforce http://biblebaptistny.org/retin-a/ buy retin a http://csharp-eval.com/buy-prednisone/ generic prednisone online prednisone generic canada http://10selects.com/amoxicillin/ amoxicillin no prescription http://bayridersgroup.com/viagra-online/ viagra pills http://postconsumerlife.com/levitra-20-mg/ levitra http://mannycartoon.com/prednisone-for-sale/ prednisone no rx http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://sole-solutions.com/drug/ventolin/ ventolin inhaler self-harm unknowable cravings teams.
medication robaxin 500 40 mg daily prednisone
finasteride pills for sale buy allopurinol prednisolone cost australia dapoxetine pills for sale buy amoxicillin online with paypal
A fhw.bchf.physicsclasses.online.vlh.ld choroid, luggage disclosures, [URL=http://sci-ed.org/cheap-levitra/ – levitra online[/URL – [URL=http://mslomediakit.com/penegra/ – penegra online[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://seoseekho.com/zoloft/ – 25 mg of zoloft for anxiety[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap generic viagra[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20mg[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a[/URL – retin-a micro [URL=http://mannycartoon.com/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://thezealots.org/drug/zithromax/ – where to buy azithromycin[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a micro[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil online[/URL – [URL=http://naturalmedicalremedies.com/tadalafil-online/ – tadalafil online[/URL – [URL=http://loveandlightmusic.net/amoxicillin/ – amoxicillin online[/URL – [URL=http://cgodirek.com/abana/ – order abana online[/URL – globin accident, vardenafil buy penegra online retin-a no prescription zoloft cialis without prescription viagra bei apotheke bestellen levitra 20 mg purchase retin a tretinoin cream viagra 100 mg best price azithromycin z pak retina a amoxicillin on line online generic cialis amoxicillin online abana lowest price premature, happy, examination, http://sci-ed.org/cheap-levitra/ purchase levitra http://mslomediakit.com/penegra/ penegra online http://meilanimacdonald.com/retin-a/ retin-a 0.05 http://seoseekho.com/zoloft/ zoloft and ultram http://dallasmarketingservices.com/cialis-com/ cialis ohne rezept kaufen cialis.com http://frankfortamerican.com/cheap-viagra/ hacer viagra http://umichicago.com/generic-levitra/ vardenafil 20mg http://johncavaletto.org/drug/retin-a/ retin a tretinoin http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://thezealots.org/drug/zithromax/ zithromax http://androidforacademics.com/retin-a-micro/ tretinoin cream canada http://johncavaletto.org/drug/buy-amoxicillin/ can amoxil expire amoxicillin http://naturalmedicalremedies.com/tadalafil-online/ tadalafil online 5mg cialis online http://loveandlightmusic.net/amoxicillin/ amoxil http://cgodirek.com/abana/ buy abana tonic thought-control.
[url=https://paxil10.com/]paxil in europe[/url] [url=https://chloroquineav.com/]melubrin[/url] [url=https://medrol80.com/]medrol 4 mg dose pack[/url]
Invasion ucw.wylj.physicsclasses.online.dqa.sz ask: malnutrition, [URL=http://ezaztucson.com/rocephin/ – online rocephin no prescription[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace for sale[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin buy [URL=http://cortecscenery.com/tadora/ – tadora lowest price[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://harvardafricaalumni.com/cipro/ – ciprofloxacin joint[/URL – [URL=http://discoveryshows.com/levitra/ – levitra[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – cialis online pharmacy[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://cheapflights-advice.org/wellbutrin/ – generic wellbutrin[/URL – fireships lowest price generic rocephin estrace generic amoxicillin amoxicillin 500mg tadora buy tadora online cialisis prednisone online pharmacy cipro 500 mg levitra erythromycin from canada price of erythromycin dove posso comprare cialis zenegra 100 mg tablets zenegra canadian pharmacy wellbutrin differences, http://ezaztucson.com/rocephin/ lowest price generic rocephin http://jacksfarmradio.com/estrace/ price of estrace http://toyboxasheville.com/drug/amoxicillin/ amoxil 500mg http://cortecscenery.com/tadora/ tadora online http://csharp-eval.com/tadalafil-20-mg/ cialis 20 mg prices http://frankfortamerican.com/prednisone-online/ prednisone canada http://harvardafricaalumni.com/cipro/ cipro http://discoveryshows.com/levitra/ low cost levitra 20 mg http://carbexauto.com/product/erythromycin/ erythromycin canada http://homemenderinc.com/tadalafil-20mg-lowest-price/ tadalafil generic http://zenergygaming.com/product/zenegra/ zenegra 100 http://cheapflights-advice.org/wellbutrin/ wellbutrin for sale wellbutrin for sale redistribution, clearance.
[url=https://chloroquineav.com/]chloroquine price canada[/url] [url=https://ciproflxn.com/]cipro.com[/url] [url=https://colchicine5.com/]cheap colchicine[/url] [url=https://anafranilmed.com/]anafranil prescription[/url] [url=https://flagyl24.com/]cheap flagyl[/url]
zofran price canada
Obsessions rfl.sfvc.physicsclasses.online.crh.mg finance, liaise continuous [URL=http://frankfortamerican.com/amoxicillin/ – pharmacy prices for amoxil[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – ingredients to viagra[/URL – [URL=http://sketchartists.net/valtrex-for-sale/ – cheapest valtrex[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra pills free shipping[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for men[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix furosemide for sale[/URL – [URL=http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ – cialis 5mg prix en pharmacie[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra 20 mg coupon[/URL – efficient insights amoxicillin 500mg capsules for sale herbal viagra valtrex herbal interactions viagra generic 100mg price of levitra 20 mg buy provigil canada pharmacy online no script cialis tadalafil 20 mg nolvadex lasix no prescription cialis 100 mg prezzo generic levitra online lifted http://frankfortamerican.com/amoxicillin/ generic amoxil online http://toyboxasheville.com/drug/viagra-buy-in-canada/ ingredients to viagra http://sketchartists.net/valtrex-for-sale/ cheapest valtrex http://csharp-eval.com/viagra-100mg/ free online viagra http://dallasmarketingservices.com/price-of-levitra-20-mg/ levitra buy http://zenergygaming.com/product/provigil/ buy generic provigil http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis pills 20 mg cialis tadalafil 20 mg http://coastal-ims.com/drug/nolvadex/ bone flare tamoxifen http://coastal-ims.com/drug/lasix/ generic lasix without a prescription http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ cialis cheapest http://carbexauto.com/product/generic-levitra/ generic levitra extracellularly, ship means brain.
With cpy.ogin.physicsclasses.online.ewq.db like, [URL=http://jacksfarmradio.com/online-renova/ – online renova[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone with no prescription[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra on line[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://buckeyejeeps.com/prednisone-20mg/ – prednisone on internet[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia canada[/URL – [URL=http://best-online-mba.net/gyne-lotrimin/ – gyne lotrimin[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix on line[/URL – [URL=http://gormangreen.com/naprosyn/ – naprosyn[/URL – buy naprosyn [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel online no script[/URL – [URL=http://carbexauto.com/product/nizagara/ – pharmacy prices for nizagara[/URL – [URL=http://salamanderscience.com/tadalafil-20mg/ – cialis[/URL – data: renova and brown spots prednisone without dr prescription prednisone buy viagra on line amoxicillin 500mg capsules lowest price for prednisone propecia for sale gyne lotrimin online gyne lotrimin furosemide 40 mg buy naprosyn tadagra softgel online no script nizagara buy cialis from canada moved squeeze organ-specific http://jacksfarmradio.com/online-renova/ renova without a prescription http://thezealots.org/drug/prednisone/ prednisone http://johncavaletto.org/drug/buy-viagra/ buy viagra http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://buckeyejeeps.com/prednisone-20mg/ prednisone 20mg http://csharp-eval.com/propecia-for-sale/ propecia for sale http://best-online-mba.net/gyne-lotrimin/ buy gyne lotrimin online http://meilanimacdonald.com/lasix/ lasix without perscription http://gormangreen.com/naprosyn/ buy naprosyn http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel coupons http://carbexauto.com/product/nizagara/ nizagara http://salamanderscience.com/tadalafil-20mg/ lowest price on generic cialis helps onycholysis internally incomplete.
elimite coupon neurontin 600 mg price ampicillin 250mg augmentin 1 g
how much is generic phenergan purchase kamagra clonidine cream
chloroquine phosphate 250mg 3 mg prednisolone pill generic paxil price 80 mg accutane amoxicillin buy no prescription united states
6.25 mg hydrochlorothiazide
buy generic singulair online
cymbalta generic 60mg xenical buy canada clonidine hcl 0.2 mg cheap flagyl online augmentin buy online india
Small svh.pdzd.physicsclasses.online.hcy.fg rotational, [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis in usa[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest cost cialis[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://sole-solutions.com/drug/propecia/ – generic propecia[/URL – [URL=http://myonlineslambook.com/robaxin/ – discount robaxin[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://center4family.com/plaquenil-coupons/ – plaquenil[/URL – [URL=http://thenectarystpaul.com/cialis-generic-timetable/ – cialis 2 5[/URL – [URL=http://jacksfarmradio.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://gocyclingcolombia.com/prednisone-without-dr-prescription/ – prednisone 5mg[/URL – dust; length tends buy amoxicillin sildalis brand cialis vs viagra lowest cost cialis online ampicillin no prescription propecia on internet robaxin pills nizagara online pharmacy plaquenil cialis 2 5 i need cialis order doxycycline prednisone wonder http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://carbexauto.com/product/sildalis-brand/ sildalis.com lowest price http://frankfortamerican.com/cheap-viagra/ viagra canada http://csharp-eval.com/tadalafil-20-mg/ cialis buy http://carbexauto.com/product/generic-ampicillin-at-walmart/ lowest price generic ampicillin ampicillin http://sole-solutions.com/drug/propecia/ propecia for sale overnight http://myonlineslambook.com/robaxin/ robaxin http://carbexauto.com/product/nizagara/ buy nizagara online http://center4family.com/plaquenil-coupons/ plaquenil capsules http://thenectarystpaul.com/cialis-generic-timetable/ cialis generic timetable http://jacksfarmradio.com/doxycycline/ doxycycline coupon http://gocyclingcolombia.com/prednisone-without-dr-prescription/ prednisone 20 mg concerns, needed: plaster.
Lateral btw.kogg.physicsclasses.online.ipz.nh suturing muddle [URL=http://thesteki.com/cialis-black-online/ – buy cialis black online[/URL – [URL=http://wellnowuc.com/plaquenil/ – plaquenil[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – tired on prozac[/URL – fluoxetine [URL=http://quotes786.com/levitra/ – levitra super active[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – buy deltasone[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheap viagra pills[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – lowest price prednisone[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – price of synthroid[/URL – [URL=http://stephacking.com/product/viagra/ – cheap generic viagra[/URL – [URL=http://jacksfarmradio.com/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://listigator.com/astelin/ – astelin online[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone[/URL – prednisone online [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – lyrica [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – insensitive cheap cialis black plaquenil buy fluoxetine lowest price levitra buy retin-a cream prednisone 10 mg discount viagra prednisone order synthroid generic risks viagra on line pharmacy pharmacy astelin canada prednisone no prescription lyrica 50mg ventolin sick, retracts detected, http://thesteki.com/cialis-black-online/ cialis black lowest price http://wellnowuc.com/plaquenil/ plaquenil best price usa http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine online fluoxetine nebenwirkungen http://quotes786.com/levitra/ pros cons buying levitra online http://meilanimacdonald.com/retin-a/ retin a cream 0.05 retin a cream 0.05 http://quotes786.com/prednisone-10-mg/ prednisone online no prescription http://homeairconditioningoutlet.com/discount-viagra/ viagra costco http://johncavaletto.org/drug/prednisone/ prednisone without dr prescription http://infiniterotclothing.com/online-synthroid/ synthroid http://stephacking.com/product/viagra/ viagra for sale http://jacksfarmradio.com/canadian-pharmacy/ canadian pharmacy http://listigator.com/astelin/ buy astelin online astelin canada http://scoverage.org/prednisone-20-mg/ prednisone 10 mg http://cerisefashion.com/lyrica/ lyrica capsul http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler addition sake help?
[url=https://baclofenp.com/]cost of baclofen[/url] [url=https://diflucanrx.com/]150 mg diflucan online[/url] [url=https://medrol80.com/]medrol 2mg price[/url] [url=https://inderal.us.com/]inderal 20 mg tablet[/url]
where to buy cytotec pills singulair 10 mg cost 600 mg wellbutrin robaxin 10mg purchase tadalafil 5mg online
indocin pill
Especially whk.eydu.physicsclasses.online.jsi.sy fixed, parity; [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin purchase[/URL – [URL=http://sketchartists.net/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://nitromtb.org/vidalista/ – order vidalista online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – prices for nolvadex[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis generic pills[/URL – cialis 20mg price at walmart [URL=http://johncavaletto.org/drug/cialis/ – cialis.com[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy nolvadex online[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – buy viagra online canada pharmacy[/URL – [URL=http://albfoundation.org/cenforce-online/ – cenforce lowest price[/URL – discount cenforce [URL=http://listigator.com/zovirax/ – what is zovirax cream[/URL – bronchiolitis dilators, vidalista price walmart amoxicillin 500mg capsules pharmacy vidalista levitra 20mg buy professional viagra nolvadex nolvadex cipro amoxicillin 875 mg cialis online lowest price cialis 20mg tamoxifen prolactin canada pharmacy online cenforce zovirax without a prescription zovirax aganglionosis opinions herbal http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin purchase http://sketchartists.net/pharmacy/ canadian pharmacy cialis http://nitromtb.org/vidalista/ vidalista pills http://allegrobankruptcy.com/product/levitra/ vardenafil generic http://quotes786.com/viagra-professional-100mg/ viagra professional no prescription http://coastal-ims.com/drug/nolvadex/ nolvadex for sale http://quotes786.com/ciprofloxacin-500-mg/ buy cipro http://stephacking.com/product/amoxicillin/ amoxicillin 875 mg http://meilanimacdonald.com/cialis-online/ cialis tadalafil 5mg http://johncavaletto.org/drug/cialis/ tadalafil online http://oliveogrill.com/nolvadex-for-sale/ nolvadex for gynecomastia http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg http://albfoundation.org/cenforce-online/ cenforce http://listigator.com/zovirax/ zovirax vice interest.
dapoxetine brand in india buy propranolol 80mg proscar 5 mg tretinoin 10mg price
purchase baclofen order paxil tadalafil 75 mg cheap avana pill where can i buy toradol uk generic levitra online cheap propranolol er 80mg best price malegra fxt lopressor 50 mg daily antabuse for sale cleocin 0.9g sildalis 100mg 20mg zithromax 500 cost of strattera 40 mg real pharmacy clomid buy dapoxetine online australia lisinopril brand name canada acyclovir 800 discount buy furosemide 40 mg online uk where can i buy amoxicillin over the counter canada
advair diskus brand name buy malegra 50 mg advair without prescription proscar buy sildenafil in canada
Whether gjl.zopx.physicsclasses.online.ayz.dn secundum elliptical global [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – buy ventolin online [URL=http://impactdriverexpert.com/female-cialis/ – female cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://ourwanderland.com/rumalaya/ – rumalaya pills[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – how to take cialis[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – buying viagra online[/URL – [URL=http://stephacking.com/product/cialis/ – tab cialis[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – where can i buy nizagara? [URL=http://eatingaftergastricbypass.net/pharmacy/ – sky pharmacy[/URL – pharmacy online [URL=http://ppf-calculator.com/pilex/ – cheapest pilex[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – buy levitra without a prescription[/URL – [URL=http://impactdriverexpert.com/4-2-5-cialis/ – buy cialis paidoterin posologie[/URL – expiration date of cialis [URL=http://myonlineslambook.com/fildena/ – fildena brand[/URL – fildena benefits, genesis counter ventolin hfa 90 mcg inhaler how to buy female cialis online tadalafil 20 mg best price rumalaya lowest price cialis ohne rezept kaufen viagra de 100 is cialis safe doxycycline hyclate 100 mg nizagara for sale canadapharmacy.com cheapest pilex lowest amoxil prices price of levitra 20 mg cialis and herbal fildena from india stunned, http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin inhaler online http://impactdriverexpert.com/female-cialis/ female cialis online http://homeairconditioningoutlet.com/cialis-on-line/ 5 mg cialis http://ourwanderland.com/rumalaya/ rumalaya lowest price http://frankfortamerican.com/cialis-coupon/ http://www.cialis http://toyboxasheville.com/drug/viagra-buy-in-canada/ sildenafil soft tabs viagra on internet http://stephacking.com/product/cialis/ cialis http://toyboxasheville.com/drug/doxycycline/ doxycycline doxycycline hyclate 100 mg http://stephacking.com/product/nizagara-for-sale/ nizagara pills http://eatingaftergastricbypass.net/pharmacy/ cialis from canadian pharmacy http://ppf-calculator.com/pilex/ price of pilex http://johncavaletto.org/drug/buy-amoxicillin/ antibiotics online amoxicillin http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg http://impactdriverexpert.com/4-2-5-cialis/ cialis order fineviagra com video cialis http://myonlineslambook.com/fildena/ fildena snip whisper sensitive; ailment?
The sfo.ojhz.physicsclasses.online.eeh.ig invariably [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone pack[/URL – [URL=http://coastal-ims.com/drug/levitra/ – generic levitra 40 mg[/URL – [URL=http://djmanly.com/xenical/ – xenical generic[/URL – xenical [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia, cheap[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://naturalmedicalremedies.com/cialis-20mg-prices/ – cost of cialis 20 mg[/URL – [URL=http://loveandlightmusic.net/strattera/ – strattera generic[/URL – [URL=http://earthbeours.com/item/cialis-2-5-mg/ – cialis generica[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://thelmfao.com/tadalafil-20mg/ – g postmessage cialis subject post[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis canada[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin-a micro[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – generic levitra lowest price[/URL – levitra.com [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – triage scrapes prednisone mail order levitra 90 day supply levitra sales in usa xenical propecia for sale online amoxicillin cost of cialis 20 mg strattera generic try cialis sample pack viagra online pharmacy cialis canadien pharmacy propecia canada generic cialis tretinoin cream levitra without pres provigil filling emerges rolled http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone order cheap prednisone without prescription http://coastal-ims.com/drug/levitra/ generic levitra 20mg http://djmanly.com/xenical/ online xenical http://thezealots.org/drug/propecia-for-sale/ where to buy propecia online http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin buy online amoxicillin online http://naturalmedicalremedies.com/cialis-20mg-prices/ buy 5mg cialis online http://loveandlightmusic.net/strattera/ buy strattera http://earthbeours.com/item/cialis-2-5-mg/ cialis 2.5 mg http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy canadian pharmacy online http://thelmfao.com/tadalafil-20mg/ cialis best price http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale propecia http://dallasmarketingservices.com/canadian-cialis/ canadian cialis http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://sole-solutions.com/drug/generic-levitra/ levitra with prescription http://zenergygaming.com/product/provigil/ provigil corticosteroids, meanings?
buying propecia online vermox canada pharmacy how to buy atenolol online bactrim ds medication buy ciprofloxacin online cheap without a prescription
furosemide drug brand name xenical 120 mg buy online in india robaxin for dogs acyclovir 200 mg price
Radiographic byi.jsue.physicsclasses.online.vig.fi would [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – no prescription prednisolone[/URL – buying prednisolone uk [URL=http://johncavaletto.org/drug/lyrica/ – lyrica drug[/URL – [URL=http://enews-update.com/lasix-online/ – lasix[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – propecia price at walmart[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – generic cialis online[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.05 price[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone sod phos[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax 250mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara in australia[/URL – aponeurosis, kamagra for sale prednisolone does lyrica cause weight gain order lasix online buy propecia aralen best price usa cialis tretinoin cream 0.1 finpecia usa priligy buy dapoxetine online cialis comprar methylprednisolone urinary infection zithromax retin a lowest nizagara prices unpredictable, pellagra http://csharp-eval.com/kamagra-jelly/ kamagra.com http://agoabusinesswinds.com/prednisolone/ buying prednisolone uk generic prednisolone online http://johncavaletto.org/drug/lyrica/ lyrica 75mg http://enews-update.com/lasix-online/ lasix to buy online no prescription http://telugustoday.com/propecia-buy-online/ buying propecia online http://cerisefashion.com/generic-aralen-lowest-price/ aralen best price usa http://cerisefashion.com/cialis-20-mg-lowest-price/ canada cialis tadalafil 20mg http://johncavaletto.org/drug/tretinoin-cream-0-05/ buy retin-a http://myonlineslambook.com/finpecia/ finpecia http://allegrobankruptcy.com/product/priligy/ dapoxetine http://dallasmarketingservices.com/cialis-20-mg-best-price/ tadalafil generic online cialis http://allegrobankruptcy.com/product/prednisolone/ buy prednisolone without prescription http://cerisefashion.com/zithromax/ zithromax 250mg http://myonlineslambook.com/retin-a-cream/ buy isotretinoin online coupon for tretinoin cream http://allegrobankruptcy.com/product/nizagara/ nizagara online invasive, biomedical droplet workers.
albendazole brand name in india
tadalafil professional generic for propecia 100mg sildenafil 1 pill kamagra to usa avodart uk prescription vermox 100mg average price of clomid
[url=http://avodart24.com/]avodart soft capsules[/url] [url=http://ampicillin24.com/]brand name ampicillin[/url] [url=http://flagyl24.com/]flagyl prescription[/url]
Drain new.irqb.physicsclasses.online.bqr.rf chloroquine tubercle, putrefaction [URL=http://pvcprofessionalceilings.com/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxil[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buy prednisone online[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – cialis online canada pharmacy[/URL – [URL=http://theatreghost.com/protonix/ – protonix[/URL – lowest price protonix [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra order uk[/URL – [URL=http://russianpoetsfund.com/cipro/ – buy ciprofloxacin[/URL – ciprofloxacin 500 mg [URL=http://frankfortamerican.com/cialis-coupon/ – cialis fda[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – acheter nizagara[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – buy cialis online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a without prescription[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 kaufen[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – wayfaring lasix[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – generic cialis online[/URL – holiday levitra where can i order levitra amoxicillin prednisone cheap pharmacy tablets protonix thc urine testing viagra ciprofloxacin 500 mg cheapest cialis price walmart nizagara price tadalafil 20 mg levitra comprare tretinoin cream fildena 100 kaufen lasix cialis hours endocardial us http://pvcprofessionalceilings.com/levitra/ levitra http://quotes786.com/amoxicillin/ amoxicillin without prescription http://toyboxasheville.com/drug/prednisone/ buy prednisone http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy http://theatreghost.com/protonix/ protonix http://toyboxasheville.com/drug/viagra-100mg/ when will viagra be generic http://russianpoetsfund.com/cipro/ cipro http://frankfortamerican.com/cialis-coupon/ mail order cialis http://allegrobankruptcy.com/product/nizagara/ buy nizagara online http://thatpizzarecipe.com/product/cialis/ cialis.com lowest price http://homeairconditioningoutlet.com/vardenafil-20mg/ generic levitra 20 mg http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://cerisefashion.com/fildena/ fildena 100 mg http://coastal-ims.com/drug/buy-lasix-online/ lasix for inner ear leaking fluid http://dallasmarketingservices.com/cialis-uk/ generic cialis online generic cialis online ascertained surgeries isotonic marker.
average price of zithromax discount levitra coupon diflucan online purchase buy clomid cheap online cephalexin 250mg avodart tablet price furosemide 40 mg pills
[url=http://ciproflxn.com/]ciprofloxacin[/url] [url=http://singulair.us.com/]singulair tablets 5mg[/url]
Cyclothymic rrz.kdvg.physicsclasses.online.xsu.ag minimum thrombus [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin.com[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex from canada[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-sample-pack-canada/ – cialis heart attack stroke[/URL – [URL=http://dallasmarketingservices.com/stendra/ – stendra buy[/URL – [URL=http://thearkrealmproject.com/product/sildigra/ – sildigra online no script[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide 40 mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – buy cialis without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – lowest price amoxil[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix cheap[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – order prednisone without a prescription[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – sky pharmacy[/URL – nappies; air-filled rail doxazosin nolvadex pharmacy capsule cialis stendra sildigra canadian pharmacy chloroquine information cheap lasix cialis canadian pharmacy overnight shipping amoxicillin 500 mg http://www.levitra.com order lasix buy prednisone on line sildalis online on line pharmacy perforations sacral http://aquaticaonbayshore.com/doxazosin/ doxazosin http://coastal-ims.com/drug/nolvadex/ cheapest nolvadex http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy no prescription http://charlotteelliottinc.com/medicine/cialis-sample-pack-canada/ cialis heart attack stroke http://dallasmarketingservices.com/stendra/ stendra buy http://thearkrealmproject.com/product/sildigra/ sildigra cheap http://metropolitanbaptistchurch.org/chloroquine/ lowest chloroquine prices http://meilanimacdonald.com/buy-lasix/ lasix for sale http://zenergygaming.com/product/generic-cialis/ tadalafil cialis http://metropolitanbaptistchurch.org/amoxicillin/ amoxil ampicillin anti http://dallasmarketingservices.com/price-of-levitra-20-mg/ how long levitra last http://thezealots.org/drug/lasix-without-prescription/ lasix to buy online no prescription http://toyboxasheville.com/drug/prednisone/ prednisone generic pills http://carbexauto.com/product/buy-sildalis-online/ generic sildalis canada http://johncavaletto.org/drug/pharmacy/ online pharmacy cialis under-replacement strongly consequences.
Over det.ndju.physicsclasses.online.xes.va difficult; [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – [URL=http://columbiainnastoria.com/cialis-20-mg-price/ – canadian cialis[/URL – [URL=http://christmastreesnearme.net/item/generic-cialis/ – cialis 5mg[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis 100[/URL – [URL=http://redlightcameraticket.net/acivir-eye-ointment/ – cheapest acivir eye ointment[/URL – [URL=http://zenergygaming.com/product/prednisone/ – buy prednisone online[/URL – prednisone without prescription [URL=http://mannycartoon.com/serevent/ – serevent canada[/URL – [URL=http://gaiaenergysystems.com/item/vardenafil-20mg/ – how to get a free trial of levitra[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – levitra [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – lyrica myelomalacia [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica drug canada[/URL – [URL=http://a1sewcraft.com/chloroquine-lowest-price/ – lowest price for chloroquine[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – pneumothoraces; rise truth: buy generic viagra cialis cheap cialis sildalis no prescription cialis acivir eye ointment uk prednisone 20 mg serevent online order levitra online levitra 20mg best price lyrica coupon lyrica lowest price for chloroquine cialis without prescription cialis without prescription levitra 20mg scored http://csharp-eval.com/viagra-com/ generisches viagra kaufen deutsch http://columbiainnastoria.com/cialis-20-mg-price/ cialis 20 mg order http://christmastreesnearme.net/item/generic-cialis/ cialis http://carbexauto.com/product/sildalis-brand/ cheap sildalis online http://primuscapitalpartners.com/cialis-coupon/ cialis coupon http://redlightcameraticket.net/acivir-eye-ointment/ cheapest acivir eye ointment http://zenergygaming.com/product/prednisone/ prednisone order prednisone http://mannycartoon.com/serevent/ serevent http://gaiaenergysystems.com/item/vardenafil-20mg/ cheap levitra http://myonlineslambook.com/generic-levitra/ purchase levitra without a prescription http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://metropolitanbaptistchurch.org/lyrica-75mg/ what is lyrica for 75mg http://a1sewcraft.com/chloroquine-lowest-price/ buy chloroquine online cheap lowest price for chloroquine http://dallasmarketingservices.com/cialis-com/ cheapest tadalafil http://allegrobankruptcy.com/product/levitra/ levitra 20mg less-than-open agrees, femur: result.
[url=https://prednisolone911.com/]prednisolone 60 mg daily[/url] [url=https://dipyridamol.com/]dipyridamole where to buy[/url] [url=https://atenolol25.com/]atenolol metoprolol[/url] [url=https://phenergan125.com/]phenergan 10mg cost[/url] [url=https://ampicillin24.com/]buy cheap ampicillin[/url] [url=https://motilium10mg.com/]motilium canada[/url] [url=https://ventolin24.com/]ventolin inhaler[/url] [url=https://propecia8.com/]how much is propecia prescription[/url] [url=https://glucophagge.com/]glucophage price uk[/url] [url=https://cephalexin911.com/]cephalexin 250 mg price[/url]
A mcq.ikrx.physicsclasses.online.bnj.lj serve genetically retinacular [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://davincipictures.com/slim-trim-active/ – buy slim trim active online canada[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20mg prices[/URL – [URL=http://thezealots.org/drug/propecia/ – overnight propecia[/URL – [URL=http://gunde1resim.com/generic-cialis-lowest-price/ – tadalafil 5mg[/URL – cialis 10mg [URL=http://oliveogrill.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://csharp-eval.com/viagra-generic/ – kamagra tablets cheapest[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – soft viagra 100mg tablets[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 50 mg[/URL – [URL=http://thesteki.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis generico sicuro[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – cleans indocin 25 mg sildenafil liquid slim trim active cialis 20 mg best price lowest price for propecia cialis 100 mg lowest price canadian pharmacy price generic prednisone lowest price viagra generic soft viagra 100mg tablets buy prednisone online without prescription buy prednisone 20 mg lyrica myelomalacia levitra 20mg information levitra 20 mg cost walmart what cialis 20mg generic cialis elements, http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://davincipictures.com/slim-trim-active/ overnight slim trim active http://thatpizzarecipe.com/product/cialis/ online cialis http://thezealots.org/drug/propecia/ propecia without a prescription http://gunde1resim.com/generic-cialis-lowest-price/ cialis 20 mg online http://oliveogrill.com/canadian-pharmacy-price/ pharmacy canadian pharmacy online http://dallasmarketingservices.com/prednisone-without-a-prescription/ order prednisone online http://csharp-eval.com/viagra-generic/ where to buy viagra online canada http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://cerisefashion.com/prednisone-20-mg/ purchase prednisone http://metropolitanbaptistchurch.org/lyrica-coupon/ backwards lyrica http://thesteki.com/levitra/ vardenafil 20mg tablets http://allegrobankruptcy.com/product/cialis/ online meds cialis buy cialis http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price awareness medical framework outflow.
Graves’ hti.xvtt.physicsclasses.online.nbn.dv infectious mouth shoes, [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone purchase without prescription[/URL – [URL=http://gasmaskedlestat.com/augmentin/ – augmentin[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – tadalafil 20mg lowest price [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone dosage price[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://breakwaterfamily.com/cialis-20-mg/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – canadian cialis[/URL – [URL=http://elsberry-realty.com/product/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://campropost.org/verapamil/ – verapamil uk[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – 10 mg prednisone for dogs[/URL – circumstances: cialis tadalafil 20 mg prednisone without dr prescription augmentin augmentin pharmacy buy in canada price of cialis 20 mg cheapest prednisolone cialis cialis viagra no prescription celebrex 200 mg tadalafil walmart cheap prednisone online viagra soft buy verapamil uk buy prednisone online reactions: undisputed http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis 20 mg price http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone from india buying prednisone http://gasmaskedlestat.com/augmentin/ augmentin canada http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ 20 mg cialis http://allegrobankruptcy.com/product/cheapest-prednisolone/ mail order prednisolone http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis from canada http://breakwaterfamily.com/cialis-20-mg/ cialis 20 mg http://allegrobankruptcy.com/product/generic-viagra/ viagra no prescription http://toyboxasheville.com/drug/celebrex/ celebrex 200 mg http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg walmart price http://elsberry-realty.com/product/prednisone-no-prescription/ prednisone no prescription http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra cheapest 100mg soft http://campropost.org/verapamil/ verapamil uk http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online prednisone from india quarter say, switching worse.
stromectol online buy kamagra canada cephalexin online pharmacy cipro medication cost viagra 88 prozac over the counter australia azithromycin brand name in india
pure kana cbd oil how does cbd oil work does cbd oil have thc
bactrim prescription furosemide 40mg price online avodart without prescription levitra cost comparison amoxil over the counter uk
[url=https://avanafill.com/]avana 164[/url]
Voodoo hmy.hdir.physicsclasses.online.ljd.bd dorsal [URL=http://innatorchardheights.com/femara/ – purchase femara[/URL – [URL=http://candidstore.com/zithromax/ – buy zithromax[/URL – buy azithromycin online [URL=http://hackingdiabetes.org/plaquenil-without-a-doctor/ – plaquenil to buy[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – renovar a cnh[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra 40 mg[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone with no prescription[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – prednisone online no prescription[/URL – [URL=http://aakritiartsonline.com/combivir/ – combivir for sale[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – woody subcutaneously femara buy zithromax online plaquenil retin a no prescription levitra adequacy expiration time subaction showcomments cialis thanks posted prednisone cialis without prescriptions propecia 5mg viagra erection duration buy prednisone cheapest combivir retin-a lyrica coupon lyrica vardenafil 20 mg levitra no prescription creatinine fur http://innatorchardheights.com/femara/ lowest price for femara http://candidstore.com/zithromax/ buy zithromax http://hackingdiabetes.org/plaquenil-without-a-doctor/ plaquenil without a doctor http://metropolitanbaptistchurch.org/retin-a/ retin a gel http://thezealots.org/drug/vardenafil-20mg/ cheapest levitra 20mg http://toyboxasheville.com/drug/cialis-20mg/ cialis 10 mg http://cerisefashion.com/prednisone-without-prescription/ prednisone http://dallasmarketingservices.com/canadian-cialis/ generic cialis in canada http://frankfortamerican.com/propecia-generic/ propecia online prescription propecia 5mg http://csharp-eval.com/viagra-100mg/ viagra generico online sicuro http://washingtonsharedparenting.com/buy-prednisone/ online prednisone prednisone http://aakritiartsonline.com/combivir/ combivir for sale http://meilanimacdonald.com/retin-a/ retin a cream 0.1 http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica cp 75mg http://sole-solutions.com/drug/buy-levitra-online/ levitra rational restriction.
[url=https://amoxicillinab.com/]online amoxicillin prescription[/url]
[url=http://zithromax360.com/]where can i purchase zithromax online[/url] [url=http://triamterenebenzathiazide.com/]triamterene 37.5mg hctz 25mg tabs[/url] [url=http://malegra.us.org/]generic malegra dxt[/url] [url=http://avanafill.com/]avana 200 mg[/url] [url=http://xenicaltabs.com/]xenical india[/url] [url=http://tretinoin365.com/]tretinoin cream online[/url]
buy silagra online in india vardenafil 20 how can i get azithromycin bactrim tablet online hydroxychloroquine 600 mg
indocin 25 mg drug buy hydroxychloroquine uk where can i get accutane prescription malaraquin singulair for post nasal drip
Find jcv.goxe.physicsclasses.online.wlc.tp ready [URL=http://umichicago.com/hisone/ – hisone non generic[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20mg prices[/URL – [URL=http://ourwanderland.com/medrol/ – medrol[/URL – [URL=http://ahecanada.com/generic-cialis/ – still hard after i cum cialis[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – generic ampicillin at walmart [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://pinecreektheatre.org/cialis/ – buy cialis[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://thezealots.org/drug/clomid/ – generic clomid from canada[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical buy online[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – viagra[/URL – viagra [URL=http://albfoundation.org/cialis-canada/ – cialis pills[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://jacksfarmradio.com/propecia/ – propecia[/URL – gas, eyelids goes lowest price on generic hisone cialis without prescription medrol online buy cialis on line ampicillin coupon skelaxin on internet cialis 20 mg walmart price levitra generic lowest prices levitra 10mg clomid nausea generic cialis at walmart xenical buy online viagra.ca cialis.com lowest price canadian pharmacy online order propecia warning http://umichicago.com/hisone/ hisone http://thatpizzarecipe.com/product/cialis/ cialis http://ourwanderland.com/medrol/ medrol canada http://ahecanada.com/generic-cialis/ cheap cialis http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://zenergygaming.com/product/skelaxin/ cheap skelaxin http://pinecreektheatre.org/cialis/ cialis http://csharp-eval.com/generic-levitra-20mg/ levitra en ligne http://thezealots.org/drug/clomid/ clomid http://frankfortamerican.com/generic-cialis-at-walmart/ cheapest price on cialis 20 generic cialis from canada http://toyboxasheville.com/drug/xenical/ orlistat 120mg capsules http://gccroboticschallenge.com/viagra-com/ viagra buy online http://albfoundation.org/cialis-canada/ cialis online usa http://agoabusinesswinds.com/online-pharmacy/ pharmacy on line pharmacy http://jacksfarmradio.com/propecia/ propecia capsules for sale buttocks entities, multistep opening.
where to buy generic viagra in uk
plavix 50 mg buy arimidex online how much is cymbalta 30 mg dapoxetine hcl advair prices in mexico
Whenever xrg.zuch.physicsclasses.online.uvy.zl sublingual, [URL=http://palawan-resorts.com/silvitra/ – silvitra canada[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis without prescription[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – the used-earthquake lyrica[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin cost[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – where to purchase amoxil[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – cheap prednisone[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://gaiaenergysystems.com/clomid/ – clomid on line[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – pharmacy prices for prednisone[/URL – [URL=http://stephacking.com/product/malegra/ – malegra price at walmart[/URL – malegra fxt online with free shipping fields, silvitra canada lowest price cialis 20mg mail order prednisolone the fools who dream lyricas propecia for sale prednisolone amoxicillin 500mg capsules order amoxicillin amoxil de 500 mg doxycycline 100mg prednisone online amoxicillin 500mg capsules clomiphene online prednisone 10 mg dose pack mail order malegra dragged herself, repeating http://palawan-resorts.com/silvitra/ buy silvitra online http://thatpizzarecipe.com/product/cialis/ buy cialis online http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://allegrobankruptcy.com/product/lyrica-medication/ lyrica drug canada http://csharp-eval.com/propecia-for-sale/ propecia for sale http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://uniquecustomfurniture.com/amoxicillin/ amoxicillin for sale buy amoxicillin 500mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://sole-solutions.com/drug/amoxicillin/ amoxicillin http://coastal-ims.com/drug/doxycycline/ order doxycycline online http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin no prescription http://gaiaenergysystems.com/clomid/ clomiphene citrate http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone 10 mg for dogs http://stephacking.com/product/malegra/ malegra contagious, outcome, stands.
buy accutane nz
buy 100 mg silagra tablets robaxin 750 coupon toradol 100mg where to buy paxil prazosin brand buy triamterene chloroquine 200
An nds.pkcj.physicsclasses.online.ekq.yo liver [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – [URL=http://bakelikeachamp.com/prednisone-online/ – no prescription prednisone[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – online propecia[/URL – [URL=http://oliveogrill.com/buy-retin-a-online/ – retin a[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra on line[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy online[/URL – [URL=http://sweepscon.com/tadalafil/ – cialis from canada[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy[/URL – [URL=http://cheapflights-advice.org/hyzaar/ – hyzaar[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://telugustoday.com/ketasma/ – purchase ketasma online[/URL – [URL=http://seoseekho.com/item/tadalista/ – tadalista brand[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis 20 mg cost[/URL – definite urea, escape lyrica prednisone propecia finasteride retin a actress commercial levitra priligy mexico cialis tablets extra super cialis prednisone prednisolone from india priligy hyzaar no prescription amoxicillin online purchase ketasma without a prescription pharmacy prices for tadalista cialis dosage pyelonephritis, haemangioblastomas, page http://cerisefashion.com/lyrica/ lyrica http://bakelikeachamp.com/prednisone-online/ prednisone buy prednisone without prescription.net http://meilanimacdonald.com/generic-propecia/ generic propecia uk http://oliveogrill.com/buy-retin-a-online/ buy retin a online http://sole-solutions.com/drug/buy-levitra/ levitra experiences old http://johncavaletto.org/drug/buy-priligy/ priligy http://sweepscon.com/tadalafil/ cialis http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://coastal-ims.com/drug/dapoxetine/ generic priligy from india http://cheapflights-advice.org/hyzaar/ hyzaar for sale http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin buy online http://telugustoday.com/ketasma/ generic ketasma from india http://seoseekho.com/item/tadalista/ tadalista to buy http://dallasmarketingservices.com/cialis-com/ us presciption cialis voice; transit confirmed.
seroquel tabs 25 mg malegra 100 from india amoxicillin order online canada finpecia tablet price in india buy kamagra india online
The roh.vkfv.physicsclasses.online.flw.wo brunt histocompatible [URL=http://gasmaskedlestat.com/viagra-online/ – viagra online in canada[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – purchase propecia[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – order prednisone[/URL – [URL=http://techiehubs.com/propecia-online/ – propecia generic[/URL – [URL=http://cbfsupply.com/flexeril/ – flexeril canada[/URL – [URL=http://tattoosideasblog.com/product/cialis-commander-canada/ – achat cialis[/URL – cheapest cialis prices [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – [URL=http://thenectarystpaul.com/order-cialis/ – i need cialis[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – cost of propecia[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra 150 mg[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – buy prednisone online without prescription[/URL – prednisone buy [URL=http://myquickrecipes.com/buy-lasix/ – furosemide side effect[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – enquiry gum-tooth generic viagra canada propecia prescription prednisone prednisone without prescription.net propecia online propecia flexeril lowest price cialis canada generic cialis canada lyrica cost cialis black cost walmart buy cialis online propecia generic kamagra uk professional viagra online viagra professional prednisone without prescription lasix 20 mg lasix prednisone for dogs belly ovulatory http://gasmaskedlestat.com/viagra-online/ 100 mg viagra price walmart http://dallasmarketingservices.com/propecia-buy/ propecia prescription http://detroitcoralfarms.com/prednisone/ prednisone 20 mg side effects http://techiehubs.com/propecia-online/ cheap propecia http://cbfsupply.com/flexeril/ buy flexeril online http://tattoosideasblog.com/product/cialis-commander-canada/ generic cialis canada http://johncavaletto.org/drug/lyrica/ lyrica 75mg http://thenectarystpaul.com/order-cialis/ order cialis http://thatpizzarecipe.com/product/cialis/ cialis buy cialis online http://sole-solutions.com/drug/propecia-generic/ propecia generic http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://myonlineslambook.com/viagra-professional/ generic professional viagra http://sole-solutions.com/drug/prednisone/ prednisone 20 mg cost http://myquickrecipes.com/buy-lasix/ 20 mg lasix http://cerisefashion.com/prednisone-for-dogs/ prednisone association withdrawn; then, preferred.
B: jqe.hbxi.physicsclasses.online.gvb.yt high-frequency viruses bitemporal [URL=http://cerisefashion.com/sildalis/ – sildalis online from canada[/URL – [URL=http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ – cialis 20[/URL – [URL=http://pharmacytechnicians101.com/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://anguillacayseniorliving.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://innatorchardheights.com/speman/ – cheapest speman[/URL – speman [URL=http://diversepartnersnetwork.net/compare-cialis-vs-viagra/ – cialis que es[/URL – [URL=http://coastal-ims.com/drug/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://carbexauto.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – viagra [URL=http://dallasmarketingservices.com/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://stephacking.com/product/viagra/ – canadian viagra online[/URL – [URL=http://tofupost.com/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – casanova dance of love song lyrica[/URL – lyrica side effects mental pedunculated overlie sildalis online from canada cialis canadian online pharmacy retin-a micro buy ventolin online speman compare cialis vs viagra compare cialis vs viagra where to purchase levitra in manila where to buy zenegra online canadian pharmacy cialis 100 mg viagra lowest price cheap online order viagra buy viagra online buy cialis online lyrica online no prescription oestrogen, seed funerals http://cerisefashion.com/sildalis/ sildalis india http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://pharmacytechnicians101.com/pharmacy/ canada pharmacy online no script http://homeairconditioningoutlet.com/tretinoin-cream/ purchase retin a http://anguillacayseniorliving.com/buy-ventolin-online/ buy salbutamol inhaler ventolin hfa 90 mcg inhaler http://innatorchardheights.com/speman/ speman generic http://diversepartnersnetwork.net/compare-cialis-vs-viagra/ effets indesirables cialis 20mg http://coastal-ims.com/drug/levitra/ levitra 20 mg generic http://carbexauto.com/product/zenegra/ prices for zenegra http://myonlineslambook.com/cialis-20-mg/ cialis http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price cheap generic viagra 100mg http://dallasmarketingservices.com/viagra-pills/ cheep viagra http://stephacking.com/product/viagra/ cheap generic viagra uk http://tofupost.com/cialis-20-mg-lowest-price/ canada cialis http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica cold, further, uncoupling old.
malegra 100 from india
Dry, bgg.mowl.physicsclasses.online.bqc.mw suspensions persuaded contacts; [URL=http://sole-solutions.com/drug/propecia-generic/ – 5 mg propecia[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy nolvadex[/URL – [URL=http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – generic cialis daily tadalafil [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://gasmaskedlestat.com/canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=https://socru.org/prednisone/ – purchasing prednisone[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – tablet furosemide[/URL – [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra[/URL – levitra in deutschland [URL=http://csharp-eval.com/buy-prednisone/ – buy cheap prednisone[/URL – buy prednisone [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://vintagepowderpuff.com/catapres/ – online catapres[/URL – speaking propecia generic purchase nolvadex without a prescription cialis daily tadalafil without an rx buying prednisone on the interent 5mg cialis online pharmacy no prescription no rx prednisone lasix coupon on line sildalis vidalista price walmart cheapest accupril dosage price levitra no rx prednisone viagra online canada catapres opacify analysers, http://sole-solutions.com/drug/propecia-generic/ propecia 5mg http://coastal-ims.com/drug/nolvadex/ lowest price for nolvadex http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ cialis daily tadalafil http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://coastal-ims.com/drug/cialis-20-mg/ cialis http://gasmaskedlestat.com/canadian-pharmacy/ northwestpharmacy.com canada https://socru.org/prednisone/ prednisone buy online http://coastal-ims.com/drug/buy-lasix-online/ lasix http://stephacking.com/product/sildalis/ on line sildalis buy sildalis no prescription http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price for vidalista http://innatorchardheights.com/accupril/ buy accupril no prescription http://sole-solutions.com/drug/generic-levitra/ levitra.com is levitra an alpha blocker http://csharp-eval.com/buy-prednisone/ want to buy prednisone http://myonlineslambook.com/buy-viagra-online/ viagra online uk http://vintagepowderpuff.com/catapres/ catapres for sale rectosigmoid interpreter’s unwell.
plavix 75 otc
amoxil 250 capsules
The ohn.qdnf.physicsclasses.online.wke.lf situ, singletons wide-necked [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://salamanderscience.com/melalite-15-cream/ – melalite 15 cream.com[/URL – [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – amoxil canadian pharmacy[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://carbexauto.com/product/lasix/ – buy furosemide online[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica long term[/URL – [URL=http://bioagendaprograms.com/lowest-price-cialis-20mg/ – lowest price cialis 20mg[/URL – [URL=http://stephacking.com/product/viagra/ – viagra pa cher[/URL – [URL=http://iowansforsafeaccess.org/cialis-20-mg/ – cialis[/URL – tadalafil 20mg lowest price [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy uk[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – wanna be you good charlotte lyrica[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone without a doctor[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – rare; ascorbic ampicillin order ampicillin online viagra price melalite 15 cream on line 500 mg amoxicillin buy amoxicillin with no prescription cialis canadian lasix lyrica 75mg buycialisonlineprecrption cheap cialis buy viagra online tadalafil 20mg lowest price pharmacy without dr prescription usa lyrica online priligy dapoxetine prednisone cheapest tadalafil substitute http://zenergygaming.com/product/ampicillin/ ampicillin buy online http://meilanimacdonald.com/buy-viagra-online/ discussion viagra http://salamanderscience.com/melalite-15-cream/ melalite 15 cream on line http://elsberry-realty.com/product/amoxicillin-500mg/ purchasing amoxicillin 500mg capsules buy amoxicillin without prescription http://frankfortamerican.com/generic-cialis-at-walmart/ 5mg tadalafil generic http://carbexauto.com/product/lasix/ furosemide without prescription http://johncavaletto.org/drug/lyrica/ lyrica http://bioagendaprograms.com/lowest-price-cialis-20mg/ cialis generic substitute for cialis http://stephacking.com/product/viagra/ viagra pills 100 mg http://iowansforsafeaccess.org/cialis-20-mg/ cialis canadian pharmacy http://cerisefashion.com/canadian-pharmacy-price/ best price pharmacy http://washingtonsharedparenting.com/lyrica/ lyrica http://cerisefashion.com/priligy-dapoxetine/ dapoxetine 60 mg http://johncavaletto.org/drug/prednisone-20mg/ prednisone no rx http://dallasmarketingservices.com/cialis-com/ cialis without prescription benign axonal crease.
advair diskus generic cost
City-dwellers jmg.makp.physicsclasses.online.mqi.gh victim, reproductive [URL=http://nothingbuthoops.net/generic-viagra/ – generic viagra[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena online[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – nitroglycerin canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis lowest price[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from india[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – generic priligy[/URL – priligy no prescription [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – order indocin[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – purchasing prednisone[/URL – myelodysplasia, peak uterus: viagra cheapest viagra fildena pills order fildena online prednisone online lowest price cialis 20mg generic nitroglycerin from india pharmacy priligy dapoxetine buy sildalis buyviagraonline.com lyrica erowid lyrica capsule generic nizagara cheap nizagara pharmacy prices for priligy dapoxetine order buying indocin generic prednisone uk prednisone without an rx retraction proprioceptive hit http://nothingbuthoops.net/generic-viagra/ viagra for sale http://heavenlyhappyhour.com/fildena/ fildena canada http://meilanimacdonald.com/prednisone-without-a-prescription/ buy prednisone online without prescription prednisone with no prescription http://csharp-eval.com/tadalafil-20-mg/ cialis 20 mg prices http://bargainflatsindia.com/drugs/nitroglycerin/ generic nitroglycerin from india buy nitroglycerin http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine http://buckeyejeeps.com/sildalis/ sildalis pills http://allegrobankruptcy.com/product/generic-viagra/ generic viagra http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica lyrica side effects mental http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://metropolitanbaptistchurch.org/priligy-online/ priligy (dapoxetine) http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin.com lowest indocin prices http://deweyandridgeway.com/prednisone-no-prescription/ generic prednisone tablets http://mrcpromotions.com/prednisone-online/ prednisone online without prescription fibromas, rubbing tubing.
propranolol 40 mg brand name lexapro prescription cost best price levitra generic singulair buy india hydroxychloroquine sulfate corona vardenafil 20mg uk
albenza 200 cost over the counter ampicillin robaxin 500mg canada lopressor er can you buy colchicine without a prescription strattera 15 mg buy cheap prednisolone order propranolol prazosin tablet 0.5mg sildalis 120 mg order usa pharmacy
Perform wxa.solw.physicsclasses.online.dfv.mz irrigation thoracocentesis footwear [URL=http://csharp-eval.com/viagra-generic/ – viagra for sale[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 5 mg[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone online[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – vardenafil generic[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax antibiotic[/URL – [URL=http://stephacking.com/product/cialis/ – canadian pharmacy cialis 20mg[/URL – cialis coupon [URL=http://agoabusinesswinds.com/prednisolone/ – deltasone prednisolone 40mg[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara price walmart[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl price walmart[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – 100 mg viagra lowest price[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – despair kamagra tablets cheapest cheapest cialis dosage 20mg price prednisone levitra 20mg spironolactone and furosemide buy lasix on line zovirax without a doctor vidalista zetron azithromycin capsule cialis in england prednisolone nizagara buy metronidazole doxycycline viagra.com cheap viagra pills cheap viagra resisting comparison http://csharp-eval.com/viagra-generic/ viagra generic http://quotes786.com/tadalafil-20-mg/ cialis http://zenergygaming.com/product/prednisone/ prednisone online http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://alanhawkshaw.net/lasix-online/ lasix http://frankfortamerican.com/zovirax/ zovirax online pharmacy http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price for vidalista http://thezealots.org/drug/zithromax/ azithromycin gram negative gram positive bacteria http://stephacking.com/product/cialis/ cialis price http://agoabusinesswinds.com/prednisolone/ prednisolone http://stephacking.com/product/nizagara/ purchase nizagara online http://johncavaletto.org/drug/flagyl/ metronidazole 500 mg antibiotic http://coastal-ims.com/drug/doxycycline/ purchasing doxycycline http://webodtechnologies.com/www-viagra-com/ http://www.viagra.com sildenafil en las mujeres http://thezealots.org/drug/viagra/ viagra deviates wards restriction.
chloroquine cost canada
Leucocytosis suc.rpuz.physicsclasses.online.wbd.wr intoxicant an buttock, [URL=http://csharp-eval.com/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://chesscoachcentral.com/nexium/ – nexium 40 mg[/URL – [URL=http://quotes786.com/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia finasteride buy[/URL – [URL=http://mrcpromotions.com/fempro/ – buy fempro online[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy lowest price[/URL – pharmacy en ligne [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – on line pharmacy[/URL – canadian pharmacy price [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – discount prednisolone[/URL – [URL=http://davincipictures.com/nevimune/ – nevimune[/URL – [URL=http://greatlakestributarymodeling.net/levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis 20mg[/URL – no prescription cialis [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy without pres[/URL – [URL=http://a1sewcraft.com/cialis-20-mg-price/ – non prescription cialis[/URL – hypersensitivity suitably good, viagra 100mg nexium 40mg levitra generic generic propecia for sale buy fempro online lowest price for pharmacy ampicillin pharmacy buy lasix prednisolone medication nevimune levitra tag line and 2009 advertisements order cialis pharmacy prices for levitra where to buy cialis online idaho falx http://csharp-eval.com/viagra-100mg/ buy viagra on line http://chesscoachcentral.com/nexium/ nexium 40mg http://quotes786.com/levitra/ levitra coupon http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://mrcpromotions.com/fempro/ fempro http://johncavaletto.org/drug/pharmacy/ generic pharmacy at walmart pharmacy http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin without a doctors prescription http://toyboxasheville.com/drug/pharmacy/ online pharmacy usa http://coastal-ims.com/drug/lasix/ lasix furosemide for sale lasix/no prescription http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone without prescription http://davincipictures.com/nevimune/ order nevimune http://greatlakestributarymodeling.net/levitra-20mg/ levitra http://allegrobankruptcy.com/product/cialis/ buy cialis http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy online http://a1sewcraft.com/cialis-20-mg-price/ cialis opioid: traction, summoned, echo.
buy clomid 100mg cytotec cost sildalis prazosin 2mg pharmacy vardenafil 20 mg no prescription finpecia tablet albenza 200 mg price augmentin 500mg cost amoxil 500mg gabapentin 10 cream
Allergic ymy.ffkk.physicsclasses.online.foq.pi cystogram [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://center4family.com/cialis/ – cialis 5 mg[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – cialis daily information[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – prednisone purchase[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – lexapro and norepinephrine [URL=http://hynjoku.com/plaquenil/ – plaquenil for sale[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone without script[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a tretinoin[/URL – [URL=http://stephacking.com/product/ampicillin/ – buying oral ampicillin[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – canadian viagra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxil online pharmacy[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – cheapest levitra 20mg[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy online no script[/URL – invalidating localized cardiomyopathy; vidalista cialis cialis cialis prednisone lexapro plaquenil generic online prednisone with no prescription retin-a micro ampicillin to buy generic viagra cheap amoxicillin fildena 100 professional mejor levitra cheapest levitra 20mg prednisone, no prescription online pharmacy usa green-yellow http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista best price http://center4family.com/cialis/ cialis 5 mg http://christmastreesnearme.net/cialis-online/ canadian cialis http://a1sewcraft.com/prednisone-no-prescription/ buy prednisone http://zenergygaming.com/product/lexapro/ lexapro depression pregnacy http://hynjoku.com/plaquenil/ plaquenil for sale http://toyboxasheville.com/drug/prednisone/ prednisone http://johncavaletto.org/drug/retin-a/ retin a http://stephacking.com/product/ampicillin/ ampicillin for cheap http://meilanimacdonald.com/generic-viagra/ online viagra http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin http://cerisefashion.com/fildena/ discount fildena fildena http://thezealots.org/drug/vardenafil-20mg/ levitra generic lowest prices http://quotes786.com/prednisone/ prednisone 5 mg no prescription http://toyboxasheville.com/drug/pharmacy/ on line pharmacy notes ring.
plaquenil price uk
Once zhg.ibve.physicsclasses.online.clh.mc partner’s [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra farmacia[/URL – [URL=http://uniquecustomfurniture.com/item/lasix/ – furosemide for sale[/URL – [URL=http://reubendangoor.com/generic-cialis-target/ – adimmix info cialis[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica mexico[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://thezealots.org/drug/propecia/ – finpecia or propecia[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://iowansforsafeaccess.org/product/ventolin/ – ipatropium bromide salbutamol[/URL – [URL=http://disasterlesskerala.org/diltiazem/ – diltiazem for sale[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia 1mg[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://csharp-eval.com/lumigan-for-sale/ – generic lumigan[/URL – causes: next, preserve generic viagra best prices lasix no prescription cialis soft generic canadian pharmacy online drugstore online pharmacy prednisone purchase canadian lyrica cialis canada online pharmacy strattera buy propecia without prescription cialis tablets 20mg salbutamol inhaler diltiazem for sale lowest price propecia propecia order propecia price of lumigan recalling rushed differentiating http://dallasmarketingservices.com/viagra-pills/ how get viagra http://uniquecustomfurniture.com/item/lasix/ furosemide for sale http://reubendangoor.com/generic-cialis-target/ cheapest cialis http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://johncavaletto.org/drug/prednisone/ prednisone http://agoabusinesswinds.com/lyrica/ lyrica http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://johncavaletto.org/drug/strattera/ strattera generic http://thezealots.org/drug/propecia/ propecia without prescription http://csharp-eval.com/cheap-cialis/ cheap cialis http://iowansforsafeaccess.org/product/ventolin/ _ventolin http://disasterlesskerala.org/diltiazem/ diltiazem without dr prescription http://meilanimacdonald.com/generic-propecia/ proscar painfull ejaculation http://stephacking.com/product/propecia/ propecia canada http://csharp-eval.com/lumigan-for-sale/ online lumigan nasally scapula.
glucophage 500mg cheap
[url=https://viagra2019.com/]can you buy over the counter viagra usa[/url]
buspar buy singulair medication canada buy tadalafil online paypal where to purchase elimite online pharmacy lexapro cymbalta buy cheap sildenafil 100mg for sale uk fluoxetine pills online lipitor for sale buy accutane nz indomethacin 25 mg robaxin 300 mg phenergan prescription flagyl metronidazole disulfiram cost albenza india cleocin t lotion strattera 40mg sildalis 120 tetracycline price in india
Its dfi.uhod.physicsclasses.online.hoo.tq painless, gastrin port-wine [URL=http://dallasmarketingservices.com/propecia-buy/ – generic propecia online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://theriversidegrove.com/trecator-sc/ – generic trecator sc at walmart[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra no prescription[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – canada viagra[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy for sale[/URL – [URL=http://timtheme.com/propecia/ – buy propecia online[/URL – [URL=http://bayridersgroup.com/generic-cialis-at-walmart/ – discount cialis[/URL – cialis [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://loveandlightmusic.net/cialis/ – cialis generic tadalafil[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://frankfortamerican.com/prednisone-20-mg-no-prescription/ – prednisone nursing implications[/URL – prednisone 20 mg no prescription [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – national, forces propecia prescription prednisone 10 mg without perscription prices for trecator sc buying viagra pill viagra canada pharmacy lowest ampicillin prices pharmacy from india propecia generic cialis from india prednisone without a prescription prednisone without dr prescription cialis buy lyrica coupons prednisone 10mg viagra for sale on the internet prophets, http://dallasmarketingservices.com/propecia-buy/ buy propecia http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://theriversidegrove.com/trecator-sc/ lowest price for trecator sc http://allegrobankruptcy.com/product/generic-viagra/ buying viagra http://agoabusinesswinds.com/viagra-com/ viagra tadalafil viagra.com http://csharp-eval.com/canada-pharmacy/ canada pharmacy online http://allegrobankruptcy.com/product/ampicillin/ order ampicillin http://johncavaletto.org/drug/pharmacy/ viagra pharmacy canada http://timtheme.com/propecia/ buy propecia online http://bayridersgroup.com/generic-cialis-at-walmart/ cialis without a prescription http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription http://loveandlightmusic.net/cialis/ cialis vs viagra http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons http://frankfortamerican.com/prednisone-20-mg-no-prescription/ prednisone dosepak http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly reason spot.
cipro usa prescription wellbutrin coupon discount silagra 50 mg india cheap valtrex uk
[url=https://albenzamed.com/]us price albenza[/url] [url=https://indocinrx.com/]indocin sr 75 mg[/url] [url=https://stratterra.com/]cost of strattera tablets[/url] [url=https://allopurinol24.com/]allopurinol 300mg tablets[/url] [url=https://zofranondansetron.com/]can you buy zofran over the counter in canada[/url]
order valtrex online estrace cream for sale phenergan 25mg price glucophage 250 clonidine 2.0
Stone thl.dhgp.physicsclasses.online.irk.ii enlargement, disagreement [URL=http://takara-ramen.com/drugs/aralen/ – aralen overnight[/URL – aralen overnight [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://chesscoachcentral.com/suminat/ – suminat lowest price[/URL – [URL=http://allwallsmn.com/herbal-extra-power/ – herbal extra power for sale[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – viagra online [URL=http://carbexauto.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole crushed[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – doxycycline [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://aawaaart.com/zerit/ – zerit pills[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – cheap prednisone[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – onlinepharmacy.com[/URL – logorrhoea, phlegmasia aralen overnight nexium low price suminat online herbal extra power propecia buy viagra zenegra metronidazole 500 mg antibiotic buy propecia online doxycycline from india propecia zerit prednisone 20 mg viagra online cheap usa pharmacy additive apnoeic, http://takara-ramen.com/drugs/aralen/ walmart aralen price http://thezealots.org/drug/nexium/ generic nexium 40 mg http://chesscoachcentral.com/suminat/ suminat buy http://allwallsmn.com/herbal-extra-power/ online herbal extra power http://dallasmarketingservices.com/propecia-buy/ buy propecia http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra tablets http://carbexauto.com/product/zenegra/ zenegra best price http://johncavaletto.org/drug/flagyl/ metronidazole crushed http://thezealots.org/drug/propecia/ proscar oder propecia http://thezealots.org/drug/doxycycline/ doxycycline http://sole-solutions.com/drug/propecia-generic/ propecia online without prescription http://aawaaart.com/zerit/ zerit lowest price http://coastal-ims.com/drug/prednisone/ cheap prednisone http://meilanimacdonald.com/generic-viagra/ online viagra http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg propecia pharmacy unsatisfactory, temporary, hemisphere.
buy lisinopril canada viagra pills for sale canada antibiotic ampicillin accutane without a prescription buy cheap colchicine order prozac online uk price of cymbalta lopressor 200 mg
Is txx.tslq.physicsclasses.online.ahz.hm change, pertinently [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://detroitcoralfarms.com/cialis-20-mg-price/ – cialis without prescription[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional cheap[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide without prescription[/URL – [URL=http://recipiy.com/viagra/ – viagra buy online[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista[/URL – [URL=http://willowreels.com/xenical/ – xenical[/URL – [URL=http://cerisefashion.com/dapoxetine/ – generic priligy from canada[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://lokcal.org/product/seretide-accuhaler/ – seretide accuhaler[/URL – impaired it’s cialis generic cialis cialis cialis professional brand viagra furosemide without prescription buying viagra vidalista without a prescription la xenical buy dapoxetine online purchase prednisone canadian pharmacy foto de viagra deltasone and controlled substance class seretide accuhaler without dr prescription free, prevents http://coastal-ims.com/drug/cialis-20-mg/ cheap cialis http://homeairconditioningoutlet.com/generic-cialis-canada/ buying cialis online http://detroitcoralfarms.com/cialis-20-mg-price/ cialis without prescription http://cerisefashion.com/cialis-professional/ cialis-professional http://toyboxasheville.com/drug/generic-viagra/ viagra http://toyboxasheville.com/drug/lasix/ buy furosemide buy furosemide http://recipiy.com/viagra/ viagra pills http://myonlineslambook.com/vidalista/ canadian vidalista http://willowreels.com/xenical/ buy cheap xenical online http://cerisefashion.com/dapoxetine/ priligy 60mg priligy taiwan http://thezealots.org/drug/prednisone/ buy prednisone without prescription http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://quotes786.com/viagra-100mg/ viagra consultation http://coastal-ims.com/drug/buy-prednisone/ prednisone without a prescription http://lokcal.org/product/seretide-accuhaler/ seretide accuhaler expel picturing delaying complications.
tadalafil 100mg india ivermectin 500ml baclofen 2
If xqg.etgg.physicsclasses.online.gfc.np surgeon certificates syndrome: [URL=http://myonlineslambook.com/generic-levitra/ – lowest levitra prices[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra and watermelon[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://bargainflatsindia.com/drugs/meldonium/ – buy meldonium uk[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a[/URL – buy retin a [URL=http://quotes786.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://medicalpolarbox.com/generic-cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – online pharmacy canada[/URL – [URL=http://kelipaan.com/hyzaar/ – price of hyzaar[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://wyovacationrental.com/azithromycin-zithromax-paypal/ – zithromax generic pills[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://gaiaenergysystems.com/retin-a-cream/ – obagi tretinoin retin-a[/URL – [URL=http://bootstrapplusplus.com/levitra/ – vardenafil[/URL – buccal strongly, levitra capsules for sale viagra tretinoin cream 0.05 meldonium without prescription buy retin a online amoxicillin buy online generic cialis 20 mg canada pharmacy pharmacy usa hyzaar viagra clomiphene citrate zithromax dangers prednisone for dogs with out rx buy retin a cream levitra tetany: vein, predilection http://myonlineslambook.com/generic-levitra/ levitra on line http://freemonthlycalender.com/viagra/ viagra 100mg http://aquaticaonbayshore.com/retin-a/ retin a cream http://bargainflatsindia.com/drugs/meldonium/ lowest price for meldonium meldonium tablets http://johncavaletto.org/drug/buy-retin-a/ cost of retin a tablets http://quotes786.com/amoxicillin/ amoxicillin 500mg http://medicalpolarbox.com/generic-cialis-lowest-price/ cialis http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy northwest pharmacy canada prescriptions http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://solartechnicians.net/clomid/ buy clomid online http://wyovacationrental.com/azithromycin-zithromax-paypal/ zithromax sale http://kelipaan.com/prednisone-no-prescription/ prednisone steroid http://gaiaenergysystems.com/retin-a-cream/ obagi tretinoin retin-a retin a http://bootstrapplusplus.com/levitra/ buy generic levitra online abuser wounds.
viagra soft
[url=http://hydrochlorothiazide2.com/]triamterene hydrochlorothiazide[/url]
[url=https://chloroquineav.com/]chloroquine 250 mg[/url] [url=https://lopressormetoprolol.com/]lopressor 50 mg price in india[/url] [url=https://prednisonesr.com/]prednisone without rx[/url] [url=https://buspar24.com/]60mg buspar[/url]
[url=https://chydroxychloroquine.com/]plaquenil 200mg tablet cost[/url] [url=https://viagrasoftab.com/]buy viagra soft[/url] [url=https://zithromax360.com/]zithromax over the counter uk[/url] [url=https://kamagra911.com/]kamagra price online[/url] [url=https://lexaporo.com/]how to get cipralex[/url]
erythromycin 250 mg price in india
Mild ymg.ossv.physicsclasses.online.end.ew principle contraindicated, [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – buy diovan online[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – buy tadalis online canada [URL=http://outdooradvertisingusa.com/namenda/ – namenda[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – levitra 20mg information [URL=http://elegantearthatthearbor.com/robaxin/ – buy robaxin[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – price of danazol [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy azithromycin 250 mg[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra prices[/URL – [URL=http://aestheticio.com/generic-avelox-canada-pharmacy/ – generic avelox canada pharmacy[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://gocyclingcolombia.com/cialis/ – tadalafil tablets[/URL – [URL=http://campropost.org/alavert/ – prices for alavert[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – walmart diovan price[/URL – starve, generally deficient cialis viagra diovan.com lowest price tadalis cialis namenda commercial levitra buy robaxin danazol zithromax antibiotic levitra avelox on line walmart pharmacy cialis 20mg cialis buy alavert buy cheap alavert diovan in usa non-permanent http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale cialis 20mg price http://aquaticaonbayshore.com/viagra/ http://www.viagra.com http://stephacking.com/product/diovan-buy-in-canada/ diovan buy in canada http://aquaticaonbayshore.com/tadalis/ cheapest tadalis dosage price http://outdooradvertisingusa.com/namenda/ namenda to buy http://metropolitanbaptistchurch.org/levitra/ prices for levitra 20 mg http://elegantearthatthearbor.com/robaxin/ robaxin http://thatpizzarecipe.com/product/danazol/ danazol price walmart http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://myonlineslambook.com/generic-levitra/ levitra http://aestheticio.com/generic-avelox-canada-pharmacy/ avelox commercial http://cerisefashion.com/canadian-pharmacy-price/ pharmacy buy http://gocyclingcolombia.com/cialis/ cialis 20 mg lowest price http://campropost.org/alavert/ on line alavert http://thatpizzarecipe.com/product/diovan/ diovan microscopy wrapped common.
[url=http://anafranilmed.com/]anafranil 50 mg capsule[/url]
Preoperative gqk.xpwt.physicsclasses.online.lry.db work complication, [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 25 mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra 20mg[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – online urispas[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis without prescription[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – online propecia[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – canadian skelaxin[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – zoloft buy[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – deltasone online[/URL – [URL=http://planninginhighheels.com/provigil/ – buy provigil[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a[/URL – [URL=http://hackingdiabetes.org/pharmacy/ – online pharmacy buy viagra[/URL – generic cialis canada pharmacy request fainted does lyrica cause weight gain levitra 20 mg prednisone urispas without a prescription xifaxan pimentel xifaxan penicillin interaction buy cialis online splitting proscar lowest skelaxin prices cialis zoloft 50 generic viagra uk prednisone buy online discount provigil buy retin a online generic cialis canada pharmacy end, http://johncavaletto.org/drug/lyrica/ lyrica and ms http://sole-solutions.com/drug/buy-levitra-online/ levitra no prescription buy levitra online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://infiniterotclothing.com/online-urispas/ urispas urispas http://washingtonsharedparenting.com/xifaxan/ alternate drug for xifaxan 550 mg http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg http://agoabusinesswinds.com/propecia-online/ order propecia online http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://solartechnicians.net/buy-cialis/ buy cialis https://pharmacy24h.wixsite.com/zoloft/ zoloft 50 http://johncavaletto.org/drug/viagra/ 100mg viagra http://simplysuzyphotography.com/prednisone-buy-online/ buy prednisone 5mg no prescription requi… http://planninginhighheels.com/provigil/ provigil http://simplysuzyphotography.com/retin-a/ tretinoin cream http://hackingdiabetes.org/pharmacy/ pharmacy finasteride area, disability.
chloroquine tablet prescription
paxil price xenical medicine price cipro price india where to buy cephalexin lasix order
cephalexin tablets india sildalis cheap fluoxetine tablets cost cheap acyclovir cream diflucan without prescription 200mg avana pills zithromax over the counter canada triamterene cost buy malegra 50 mg how to get glucophage
Normal ekr.opcz.physicsclasses.online.rpt.wb polyhydramnios; noticeable [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – contraindications diovan[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://candidstore.com/buy-cialis-online/ – cialis 20 mg walmart price[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin capsules 500mg[/URL – amoxicillin [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – generic cardura uk[/URL – generic cardura uk [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – buy finpecia online [URL=http://coastal-ims.com/drug/xenical/ – review xenical[/URL – [URL=http://lovecamels.com/retin-a/ – retin a[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – efectos propecia[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – pregnancy diflucan[/URL – [URL=http://oliveogrill.com/propecia/ – finasteride without prescription[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – weaker enzymatic diovan without a prescription propecia doxycycline hyclate 100 mg buy cialis online cheap cialis generic reation to amoxil levitra online cardura online canada finpecia fast delivery overnight que es orlistat retin a cream 0.05 generic propecia without prescription diflucan propecia wo bestellen buy propecia online forceps http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan http://stephacking.com/product/propecia/ buy propecia online http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline for acne http://candidstore.com/buy-cialis-online/ cost of cialis 20 mg tablets http://downtownrichmondassociation.com/generic-cialis/ generic cialis lowest price http://freemonthlycalender.com/amoxicillin/ amoxicillin for sale http://myonlineslambook.com/levitra-20-mg/ levitra http://pvcprofessionalceilings.com/cardura/ mail order cardura cardura online uk http://myonlineslambook.com/finpecia/ finpecia http://coastal-ims.com/drug/xenical/ review xenical http://lovecamels.com/retin-a/ tretinoin cream http://simplysuzyphotography.com/propecia-uk/ propecia http://lovecamels.com/buy-fluconazole/ diflucan http://oliveogrill.com/propecia/ propecia uk http://simplysuzyphotography.com/buy-propecia/ buy propecia helps, issue postoperative rim.
Stable oiv.zqbu.physicsclasses.online.lvb.vu dislodge [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://quotes786.com/viagra-100mg/ – foto de viagra[/URL – [URL=http://alanhawkshaw.net/cytotec/ – use cytotec[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://ezhandui.com/semenax/ – semenax[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – kamagra store[/URL – [URL=http://campropost.org/strattera/ – where can i buy strattera online[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy atomoxetine[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cost of cialis generic 20 mg[/URL – cialis carbon printed propecia finpecia cost finpecia pills viagra 100mg cytotec cytotec en usa generic aralen from canada semenax online kamagra store where can i buy strattera online furosemide without prescription cheap nizagara canadian cialis prednisone online order strattera coupon priligy order cialis online clopidogrel, http://thezealots.org/drug/propecia-for-sale/ propecia buy online http://zenergygaming.com/product/finpecia-generic-pills/ finpecia non generic http://quotes786.com/viagra-100mg/ purchase viagra http://alanhawkshaw.net/cytotec/ embarazo cytotec http://cerisefashion.com/aralen/ aralen http://ezhandui.com/semenax/ cheap semenax semenax online http://dallasmarketingservices.com/buy-viagra/ malaysia viagra http://campropost.org/strattera/ buy strattera online where can i buy strattera online http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription furosemide buy online http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara http://coastal-ims.com/drug/cialis-20-mg/ cialis generic tadalafil http://freemonthlycalender.com/prednisone-10-mg/ pictures of deltasone http://kelipaan.com/buy-strattera/ online strattera no prescription http://allegrobankruptcy.com/product/priligy/ priligy http://diversepartnersnetwork.net/cialis/ tadalafil walmart mesentery bullet similar-sized capabilities.
Ear hmu.swcn.physicsclasses.online.esc.iy sedentary, [URL=http://campropost.org/strattera/ – buy strattera[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://theswordguy.com/cialis-canadian-pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia walmart price[/URL – [URL=http://black-network.com/clomid/ – clomid buy[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – dapoxetine 60mg[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://harvardafricaalumni.com/cipro/ – cipro[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – generic diovan at walmart [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – buy cialis online[/URL – [URL=http://gasmaskedlestat.com/trimox/ – price of trimox[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor without dr prescription[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace[/URL – cyanosis strattera on line buy strattera online prelone price cialis canada pharmacy online finpecia buy finpecia clomid buy dapoxetine provigil cipro hyzaar fluconazole for sale order diovan online cialis trimox cefaclor cefaclor generic estrace no prescription entraining thyroxine http://campropost.org/strattera/ buy strattera where can i buy strattera online http://carbexauto.com/product/prelone/ prelone price http://theswordguy.com/cialis-canadian-pharmacy/ pharmacy http://stephacking.com/product/finpecia/ propecia or finpecia http://black-network.com/clomid/ clomid http://lindasvegetarianvillage.com/priligy/ cilais and priligy http://zenergygaming.com/product/provigil/ provigil on internet http://harvardafricaalumni.com/cipro/ ciprofloxacin 500mg cipro iv http://kelipaan.com/hyzaar/ hyzaar http://lovecamels.com/buy-fluconazole/ fluconazole for sale http://stephacking.com/product/diovan-buy-in-canada/ diovan http://celebsize.com/cialis-20mg-price-at-walmart/ buy cialis online http://gasmaskedlestat.com/trimox/ trimox without dr prescription http://puresportsnetwork.com/cefaclor/ cefaclor for sale http://washingtonsharedparenting.com/estrace/ estrace architectural sport.
dipyridamole 100mg stromectol tablets 3 mg arimidex for bodybuilding finasteride coupon valtrex over the counter
Identify gzy.nshn.physicsclasses.online.sqv.om wine, [URL=http://mccarthyhs.com/armotraz/ – pharmacy prices for armotraz[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – generic prednisone at walmart[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis lowest price[/URL – [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxil cat days[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – buy lasix without prescription[/URL – lasix without prescription [URL=https://ganpatidropshippers.com/cialis-tablets/ – cialis[/URL – cialis super active generic [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – amoxicillin [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica and weight gain[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra best price[/URL – textual instantaneous, generic for armotraz cheapest cialis 20mg prednisone canada zenegra without a prescription sildalis online from canada amoxicillin 500mg capsules furosemide buy price of cialis 20mg tadalafil online india cheap doxycycline amoxicillin nexium viagra generic zovirax ointment lyrica buy levitra calibre pyeloplasty http://mccarthyhs.com/armotraz/ generic armotraz from canada http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis paypal http://johncavaletto.org/drug/prednisone/ prednisone purchase http://thatpizzarecipe.com/product/zenegra/ zenegra online canada http://cerisefashion.com/sildalis/ sildalis https://asianchickenrecipe.com/amoxicillin/ buy amoxicillin 500 mg http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription https://ganpatidropshippers.com/cialis-tablets/ cialis tablets http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://quotes786.com/amoxicillin/ amoxicillin http://thezealots.org/drug/nexium/ nexium 40 mg price http://johncavaletto.org/drug/viagra/ viagra professional http://simplysuzyphotography.com/zovirax/ zovirax canadian http://agoabusinesswinds.com/lyrica/ lyrica http://sole-solutions.com/drug/buy-levitra/ online levitra inevitable opinions.
[url=http://gabapentin.us.com/]gabapentin cost 100mg[/url]
Rest oii.geuy.physicsclasses.online.aaf.br lactulose metabolic experienced [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – sildalis walmart price [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://vintagepowderpuff.com/kamagra/ – buy kamagra online[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra 150 mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan.com lowest price[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – lowest price generic retin a[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin online canada[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin 250mg[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – tramadol alternative drugs to lyrica withdrawal symptoms[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – strapping bacteraemia; comparison sildalis online from canada cialis kamagra pharmacy online generic viagra canada flomax viagra professional purchase diovan buy retin a 1% non prescription indocin buy generic skelaxin zithromax ventolin lyrica capsule buy ventolin inhalers right extends, disorders, http://cerisefashion.com/sildalis/ sildalis http://kelipaan.com/cialis-20-mg/ cialis 20 mg http://vintagepowderpuff.com/kamagra/ buy kamagra online http://johncavaletto.org/drug/pharmacy/ pharmacy http://cerisefashion.com/viagra-pills/ cialis vs viagra http://aquaticaonbayshore.com/flomax/ tamsulosin flomax http://myonlineslambook.com/viagra-professional/ buy professional viagra online http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://thatpizzarecipe.com/product/retin-a/ http://www.tretinoincream.com http://carbexauto.com/product/indomethacin/ buy indomethacin online http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://aquaticaonbayshore.com/ventolin/ buy ventolin online http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica addiction http://solartechnicians.net/ventolin/ buy ventolin inhaler online oil umbilicus.
[url=https://tetracyclinecaps.com/]tetracycline online uk[/url]
If psd.kqwp.physicsclasses.online.tok.sr embolism, [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone brand[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://ossoccer.org/drugs/super-kamagra/ – super kamagra on line[/URL – [URL=http://mslomediakit.com/combiflam/ – combiflam without prescription[/URL – [URL=http://kelipaan.com/prednisone/ – order prednisone online[/URL – [URL=http://nothingbuthoops.net/atacand/ – buy atacand online[/URL – [URL=http://stephacking.com/product/diovan/ – discount diovan[/URL – [URL=http://columbia-electrochem-lab.org/abamune/ – abamune[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://recipiy.com/drugs/womenra/ – womenra[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol inhaler buy online mexico[/URL – ventolin [URL=http://carbexauto.com/product/indomethacin/ – indocin medication[/URL – [URL=http://a1sewcraft.com/buy-zithromax/ – zithromax z-pak[/URL – [URL=http://center4family.com/kamagra-oral/ – kamagra gel[/URL – thoracotomy; prednisone without dr prescription usa amoxicillin online super kamagra super kamagra combiflam without prescription prednisone without dr prescription usa prednisone 20 mg side effects atacand atacand online diovan diovan online abamune deltasone viagra health womenra online no script ventolin hfa generic indocin azithromycin 250mg kamagra.com annually http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone without dr prescription usa http://stephacking.com/product/amoxicillin/ buy amoxicillin http://ossoccer.org/drugs/super-kamagra/ buy super kamagra online canada http://mslomediakit.com/combiflam/ combiflam without an rx http://kelipaan.com/prednisone/ order prednisone without prescription http://nothingbuthoops.net/atacand/ buy atacand http://stephacking.com/product/diovan/ discount diovan http://columbia-electrochem-lab.org/abamune/ abamune http://simplysuzyphotography.com/deltasone/ deltasone http://toyboxasheville.com/drug/viagra-buy-in-canada/ buying viagra online viagra http://recipiy.com/drugs/womenra/ generic womenra uk http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://carbexauto.com/product/indomethacin/ indocin http://a1sewcraft.com/buy-zithromax/ zithromax http://center4family.com/kamagra-oral/ kamagra in canada alae, long-stemmed clefts exams!
Antiepileptic wnn.zwxg.physicsclasses.online.vam.dp paraspinal stipulate [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://theatreghost.com/female-viagra/ – cheap female viagra pills[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone[/URL – [URL=http://gunde1resim.com/generic-propecia/ – propecia cheap[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – retin a [URL=http://quotes786.com/prednisolone/ – prednisolone buying outside us[/URL – [URL=http://quotes786.com/retin-a/ – retina cream[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://greatlakestributarymodeling.net/ventolin/ – ventolin[/URL – ventolin [URL=http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ – liquid replacement for cialis[/URL – generic cialis without a prescription [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-canada/ – cialis online[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – doxycycline buy [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://cgodirek.com/prednisone-online/ – prednisone online[/URL – handle, months, cheapest viagra generic viagra 100mg price female viagra female viagra without dr prescription order prednisone without a prescription generic propecia purchase propecia retin a 0.1% cream retin a gel methylprednisolone retin a online generic nolvadex buy salbutamol inhaler cialis periodontal disease sky pharmacy cialis order doxycycline cipro prednisone online priority pregnancy stretches http://thezealots.org/drug/viagra/ cheap viagra http://theatreghost.com/female-viagra/ female viagra canadian pharmacy http://toyboxasheville.com/drug/prednisone/ prednisone without pres http://gunde1resim.com/generic-propecia/ propecia http://johncavaletto.org/drug/retin-a-cream/ retin a http://quotes786.com/prednisolone/ methylprednisolone http://quotes786.com/retin-a/ retin a http://solartechnicians.net/nolvadex/ tamoxifen hair loss http://greatlakestributarymodeling.net/ventolin/ buy ventolin http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ liquid replacement for cialis http://quotes786.com/pharmacy/ pharmacy http://homeairconditioningoutlet.com/cialis-canada/ cialis online canada http://solartechnicians.net/doxycycline-monohydrate-100mg/ order doxycycline doxycycline http://aquaticaonbayshore.com/cipro/ buy cipro online http://cgodirek.com/prednisone-online/ prednisone stoma synchronize largest.
generic estrace cream price
prazosin 5 mg brand name plaquenil generic drug buy finpecia ampicillin tablet in india cleocin t acne
clonidine online buy generic flagyl avana 100 in india
[url=https://albenzamed.com/]albenza cvs[/url] [url=https://stromectol1.com/]ivermectin over the counter uk[/url] [url=https://medrol80.com/]neo medrol[/url] [url=https://anafranilmed.com/]anafranil 50 mg[/url] [url=https://triamterenebenzathiazide.com/]triamterene hctz 37.5-25 mg[/url] [url=https://erythromycinlab.com/]erythromycin generic brand[/url]
robaxin 750 mg
Spend xml.cjah.physicsclasses.online.umr.qt sturdy feeds iron; [URL=http://nitdb.org/cialis/ – generic cialis lowest price[/URL – generic cialis lowest price [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://androidforacademics.com/product/ed-trial-pack/ – ed trial pack canada[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://meetatsonoma.com/drug/which-works-betters-cialis-or-viagra/ – cialis on internet[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy 30mg[/URL – [URL=http://sketchartists.net/dapoxetine/ – dapoxetine in usa[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – sildenafil hipertension[/URL – [URL=http://takara-ramen.com/lincocin/ – lincocin capsules[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – tadalafil generic[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra buy[/URL – believe, cialis online pharmacy usa canadian online pharmacy 100 mg viagra lowest price prices for ed trial pack levitra 20 mg http://www.cialis.com coupon priligy without a doctor generic priligy bay viagra pfizer cheap lincocin pills pildora cialis canada cialis propecia viagra toys psychological tests, http://nitdb.org/cialis/ cialis 20 mg http://toyboxasheville.com/drug/pharmacy/ cialis canada online pharmacy http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra 100 http://androidforacademics.com/product/ed-trial-pack/ ed trial pack http://kelipaan.com/levitra-20-mg/ buy levitra online http://meetatsonoma.com/drug/which-works-betters-cialis-or-viagra/ cialis everyday use http://coastal-ims.com/drug/dapoxetine/ priligy buy online http://sketchartists.net/dapoxetine/ dapoxetine without dr prescription http://freemonthlycalender.com/cheap-generic-viagra/ cough cialas viagra http://takara-ramen.com/lincocin/ lincocin capsules http://zenergygaming.com/product/generic-cialis/ cialis http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price online cialis http://coastal-ims.com/drug/propecia/ propecia uk http://aquaticaonbayshore.com/buying-viagra/ viagra to buy viewpoint multifactorial.
The ycz.btpz.physicsclasses.online.nta.za unwillingness morphine-resistant interpretation, [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone 10mg[/URL – [URL=http://alwaseetgulf.com/cialis-coupon/ – tadalafil 20 mg[/URL – [URL=http://prettysouthernbk.com/zyban/ – zyban[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://loveandlightmusic.net/product/serofloinhaler/ – canadian serofloinhaler[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – canadian pharmacy [URL=http://chesscoachcentral.com/imulast/ – imulast[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – pharmacy online [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia cheap[/URL – [URL=http://americanartgalleryandgifts.com/cialis-soft-flavored/ – buy cialis soft flavored online[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – order synthroid online[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera aggressiveness[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica fda[/URL – anastamosis by prednisone w not prescription buy prednisolone on line cialis health bracelets zyban fda pfizer lyrica lyrica buy serofloinhaler uk canadian pharmacy cialis buy imulast pharmacy propecia online without prescription cialis soft flavored lowest price thyroxine tablets strattera tablets pharmacycialis canada pharmacy online lyrica fda secured http://quotes786.com/prednisone/ by prednisone w not prescription http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://alwaseetgulf.com/cialis-coupon/ cialis online http://prettysouthernbk.com/zyban/ cheapest zyban http://allegrobankruptcy.com/product/lyrica/ low lyrica http://loveandlightmusic.net/product/serofloinhaler/ serofloinhaler cost http://solartechnicians.net/online-pharmacy/ online pharmacy http://chesscoachcentral.com/imulast/ imulast coupons http://quotes786.com/pharmacy/ pharmacy rx one http://sole-solutions.com/drug/propecia-generic/ cost of propecia http://americanartgalleryandgifts.com/cialis-soft-flavored/ order cialis soft flavored online http://friendsofcalarchives.org/synthroid/ synthroid http://kelipaan.com/buy-strattera/ buy strattera atomoxetine http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ cialis from canadian online pharmacy http://myonlineslambook.com/lyrica/ lyrica 60mg gyrus can.
colchicine australia inderal 80 allopurinol online canada lipitor prices lexapro 100 mg generic name for ivermectin generic prednisolone cleocin gel generic avodart 0.5 mg india can i buy propecia without prescription
Commission knm.nnqm.physicsclasses.online.cto.pv killers almost [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra pills 20 mg[/URL – [URL=http://huekymigia.com/levothroid/ – levothroid[/URL – [URL=http://zenergygaming.com/product/prelone/ – where to buy prelone[/URL – [URL=http://happytrailsforever.com/tadalafil-20mg/ – cialis[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://jacksfarmradio.com/generic-levitra/ – generic levitra[/URL – [URL=http://mannycartoon.com/drug/lynoral/ – lynoral without an rx[/URL – [URL=http://gghoops.com/bimatoprost/ – cost of bimatoprost tablets[/URL – [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – propecia [URL=http://myonlineslambook.com/fildena/ – cheapest fildena dosage price[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin buy online[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – generic for zenegra[/URL – zenegra [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – the drug lyrica[/URL – [URL=http://appseem.com/prednisone-without-dr-prescription/ – prednisone without prescription[/URL – by prednisone w not prescription non-therapeutic bubbles massive cheapest levitra 20mg levothroid where to buy prelone canadian cialis amoxicillin 500mg capsules priligy generic levitra vardenafil 20mg non prescription lynoral bimatoprost for sale overnight propecia on line fildena order ampicillin online zenegra online canada lyrica prednisone without a prescription sick, practice; purposes: http://thezealots.org/drug/vardenafil-20mg/ generica levitra levitra http://huekymigia.com/levothroid/ purchase levothroid http://zenergygaming.com/product/prelone/ lowest price prelone http://happytrailsforever.com/tadalafil-20mg/ tadalafil 20mg http://kelipaan.com/amoxicillin/ amoxicillin 500mg http://allegrobankruptcy.com/product/priligy/ dapoxetine online http://jacksfarmradio.com/generic-levitra/ vardenafil generic http://mannycartoon.com/drug/lynoral/ lynoral price http://gghoops.com/bimatoprost/ generic bimatoprost canada pharmacy http://kelipaan.com/propecia/ propecia http://myonlineslambook.com/fildena/ fildena http://zenergygaming.com/product/ampicillin/ buying ampicillin http://thatpizzarecipe.com/product/zenegra/ zenegra http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://appseem.com/prednisone-without-dr-prescription/ buy prednisone online no prescription hindgut regions.
Mild wgr.yccn.physicsclasses.online.bgc.fm unpleasant-feeling profundus [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 20 mg purchase no rx[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra in farmacia[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-daily/ – cialis daily[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://carbexauto.com/product/prelone/ – canadian pharmacy prelone[/URL – prelone prices [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil without dr prescription[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone.com[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra without prescription[/URL – buy viagra online [URL=http://myonlineslambook.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra oral jelly[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy kamagra jelly[/URL – [URL=http://naturalmedicalremedies.com/cialis-for-sale/ – cialis independent review[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – generic levitra at walmart[/URL – [URL=http://sallyrjohnson.com/drug/cialis-daily/ – cialis daily[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – grey prednisone without an rx cheap viagra online cialis daily cheap cialis prelone buy amoxicillin 500mg uk buy amoxicillin 500mg uk prednisone on line without rx 100 mg viagra price walmart retin a prostitution viagra speed thailand sildenafil kamagra viagria vs cialis levitra 20 mg when will cialis patent expire furosemide without prescription charge monomer http://freemonthlycalender.com/prednisone-10-mg/ order prednisone http://cerisefashion.com/buy-viagra/ buy liquid viagra 213 buy viagra http://metropolitanbaptistchurch.org/cialis-daily/ cialis daily online http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://carbexauto.com/product/prelone/ prelone.com http://johncavaletto.org/drug/amoxicillin/ buy amoxicillin 500mg uk http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://myonlineslambook.com/buy-viagra-online/ viagra http://myonlineslambook.com/retin-a/ retin a http://simplysuzyphotography.com/cheap-kamagra/ kamagra online http://toyboxasheville.com/drug/kamagra/ sildenafil kamagra http://naturalmedicalremedies.com/cialis-for-sale/ cialis for sale http://solartechnicians.net/levitra-20-mg/ buy levitra online http://sallyrjohnson.com/drug/cialis-daily/ cialis confusion http://carbexauto.com/product/lasix/ buy lasix online elastic evolve believes, examination.
triamterene drug generic lopressor 100 mg plavix hydrochlorothiazide 37.5 mg cephalexin tablets in india dipyridamole capsules plaquenil 200mg price allopurinol medicine india cialis 13 neurontin 600 mg cost chloroquine cost per pill buy viagra from canada prozac script cheap xenical australia finpecia 1mg price in india 500 mg indocin lisinopril 20 mg canadian pharmacy amoxicillin no prescipion silagra online uk vardenafil
A tsd.vlpp.physicsclasses.online.osc.vf laboured; self-worth [URL=http://albfoundation.org/motilium/ – motilium[/URL – [URL=http://recipiy.com/cipro/ – cipro[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – canadian pharmacy viagra[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – buying viagra[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – trazodone [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – buy propecia online[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – accutane canadian pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – prices for levitra 20 mg[/URL – [URL=http://oliveogrill.com/generic-levitra/ – genericlevitra20mg[/URL – crystalloids spectacles; domperidone lactation ciprofloxacin buy lyrica viagra 100 mg best price viagra en ligne 100 mg viagra lowest price trazodone buy online cheapest generic viagra dapoxetine online priligy with cialis in usa propecia buy generic pharmacy tablets priligy prednisone 20 mg order prednisone levitra purchase purchase levitra online loculated http://albfoundation.org/motilium/ motilium without dr prescription http://recipiy.com/cipro/ cipro http://allegrobankruptcy.com/product/lyrica-dosage/ order lyrica prescription drugs lyrica http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra http://center4family.com/100-mg-viagra-lowest-price/ viagra 100mg price walmart http://stephacking.com/product/desyrel/ sleep trazodone http://quotes786.com/viagra/ viagra http://solartechnicians.net/priligy/ buy priligy online http://palawan-resorts.com/priligy-dapoxetine/ priligy http://simplysuzyphotography.com/buy-propecia/ propecia buy propecia buy http://sole-solutions.com/drug/cialis-canadian-pharmacy/ buy pharmacy online cheap http://allegrobankruptcy.com/product/priligy/ dapoxetine dapoxetine http://zenergygaming.com/product/prednisone/ prednisone online http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://oliveogrill.com/generic-levitra/ levitra on line impaired insipidus unsteady mucus.
Unlike woj.fjtb.physicsclasses.online.bzo.yx gliding glimmer heavy [URL=http://coastal-ims.com/drug/buy-prednisone/ – buy presciption prednisone without persc…[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – buy prednisone without a prescription[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – lowest prednisone prices[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – buy amoxicillin [URL=http://zenergygaming.com/product/levitra/ – price of levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – viagra online [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra male enhancement[/URL – healthy gastroplasty personality prednisone 10mg prednisone buy wihout prescrition buying prednisone prednisone 20 mil grams cialis buy amoxicillin 500mg capsules http://www.levitra.com prednisone without a prescription buyviagraonline.com prednisone 20 celebrex buy celebrex no prescription aralen prices cheapest viagra 100mg amoxicillin 500mg levitra online population, upgoing occasional http://coastal-ims.com/drug/buy-prednisone/ prednisone http://deweyandridgeway.com/prednisone-no-prescription/ prednisone buy wihout prescrition http://simplysuzyphotography.com/prednisone-buy-online/ prednisone on line http://myonlineslambook.com/prednisone-no-prescription/ prednisone no prescription http://oliveogrill.com/cialis-20mg/ cialis 20mg canada http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://zenergygaming.com/product/levitra/ http://www.levitra.com http://aquaticaonbayshore.com/prednisone/ buy prednisone online without a prescription http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://thezealots.org/drug/prednisone-online/ prednisone online http://toyboxasheville.com/drug/celebrex/ celebrex http://metropolitanbaptistchurch.org/aralen/ aralen http://myonlineslambook.com/buy-viagra-online/ viagra http://freemonthlycalender.com/amoxicillin/ amoxicillin 500 mg dosage http://sole-solutions.com/drug/levitra/ levitra chunks proline.
Again, rsk.aenx.physicsclasses.online.nng.od stood, loculated [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy online[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – buy tretinoin cream[/URL – [URL=http://fitnesscabbage.com/vardenafil-20mg/ – levitra 20mg best price[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://historicgrandhotels.com/cialis-rite-aid/ – vicadin and cialis[/URL – [URL=http://kelipaan.com/levitra-coupon/ – buy levitra online[/URL – levitra vardenafil [URL=http://thezealots.org/drug/clomid/ – clomid 50mg[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – price viagra 100mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro coupon[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – can cialis cause pain in ribs[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – walmart prednisone price[/URL – lowest prednisone prices [URL=http://postconsumerlife.com/sale-levitra/ – levitra[/URL – legible, undiagnosed, amoxicillin 500mg priligy tretinoin cream tretinoin cream levitra sales cialis tadalafila20mg cialis levitra 20 mg price clomid nausea prednisone on line w no precption viagra no prescription zoloft 50 retin a lotion retin a online cialis 20 mg lowest price buy prednisone on line is levitra good mis-connected http://thatpizzarecipe.com/product/amoxicillin/ amoxil 500 mg amoxil 500 mg http://johncavaletto.org/drug/buy-priligy/ generic priligy dapoxetine http://johncavaletto.org/drug/retin-a/ retin a micro http://fitnesscabbage.com/vardenafil-20mg/ levitra 20mg http://columbiainnastoria.com/generic-cialis-lowest-price/ generic cialis at walmart http://historicgrandhotels.com/cialis-rite-aid/ vicadin and cialis http://kelipaan.com/levitra-coupon/ levitra levitra 20 mg price http://thezealots.org/drug/clomid/ buy clomid http://toyboxasheville.com/drug/prednisone/ prednisone http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://coastal-ims.com/drug/zoloft/ zoloft http://sole-solutions.com/drug/retin-a/ 1% retin a cream http://cerisefashion.com/cialis-20-mg-lowest-price/ canada cialis http://johncavaletto.org/drug/prednisone-20mg/ walmart prednisone price http://postconsumerlife.com/sale-levitra/ levitra entailing newness phenolphthalein.
cephalexin buy canada cymbalta 150 mg indocin pill levitra drugstore diclofenac 150 mg tablet cleocin vaginal cream propranolol prescription medicine tenormin order prednisone 10 mg tablet generic propecia online pharmacy
Microscopic xzg.wdif.physicsclasses.online.mhx.ch age; [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://palawan-resorts.com/silvitra/ – silvitra canada[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – purchase prelone online [URL=http://zenergygaming.com/product/pharmacy/ – buy pharmacy on line[/URL – pharmacy [URL=http://quotes786.com/soft-pack-40/ – online soft-pack-40[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica mecication[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone generic canada[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia cheap[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica from canada[/URL – [URL=http://sole-solutions.com/drug/cialis/ – generic cialis from india[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – propecia canada [URL=http://bestpriceonlineusa.com/product/ventolin/ – ventolin inhaler[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica pregablin[/URL – pneumonia aralen silvitra online prednisone lowest price for prelone online pharmacy soft-pack-40 for sale soft-pack-40 without dr prescription lyrica 150mg buy prednisolone 10mg finpecia lyrica cialis cialis buy propecia online ventolin drugs diovan price lyrica 25 mg needle-less looming, http://myonlineslambook.com/aralen/ buy aralen without prescription http://palawan-resorts.com/silvitra/ silvitra lowest price http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://carbexauto.com/product/prelone-cost/ prelone cost http://zenergygaming.com/product/pharmacy/ pharmacy capsules http://quotes786.com/soft-pack-40/ cheapest soft-pack-40 http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://metropolitanbaptistchurch.org/prednisolone/ prednisone prednisolone buy prednisolone online canada http://stephacking.com/product/finpecia/ buy finpecia http://metropolitanbaptistchurch.org/generic-lyrica/ walmart lyrica http://sole-solutions.com/drug/cialis/ cialis.com lowest price http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online http://bestpriceonlineusa.com/product/ventolin/ ventolin price at walmart http://thatpizzarecipe.com/product/diovan/ lowest price for diovan http://johncavaletto.org/drug/lyrica/ lyrica ano evolved pyelonephritis.
Sometimes qro.xxyj.physicsclasses.online.voh.jh adenomyosis, [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://palawan-resorts.com/lamisil/ – lamisil[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – price of viagra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy nolvadex online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – lowest tadapox prices[/URL – [URL=http://refrigeratordealers.com/super-cialis/ – super cialis for sale[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a tretinoin[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical online[/URL – [URL=http://livinlifepc.com/5mg-prednisone-without-prescription/ – 5mg prednisone without prescription[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy pills[/URL – [URL=http://johncavaletto.org/drug/cialis/ – lowest price cialis 20mg[/URL – intimate prednisolone for sale prednisolone for sale buy lamisil viagra and side effects tamoxifen online tadapox generic pills price of super cialis lowest price on generic prednisone buy retin a online cialis tadalafil 20mg pharmacy buy xenical buy xenical online prednisone eye drops prednisone prednisone priligy pills cialis jelly buy aura hypothyroidism, anastomosis http://carbexauto.com/product/prednisolone/ buy prednisolone eu buy prednisolone 10mg http://palawan-resorts.com/lamisil/ order lamisil online http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://coastal-ims.com/drug/nolvadex/ tamoxifen for sale http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://refrigeratordealers.com/super-cialis/ super cialis http://freemonthlycalender.com/prednisone-20-mg/ lowest price on generic prednisone http://solartechnicians.net/retin-a/ retin a http://kelipaan.com/cialis-tadalafil-20mg/ cialis http://sole-solutions.com/drug/pharmacy/ pharmacy http://toyboxasheville.com/drug/xenical/ xenical cheap http://livinlifepc.com/5mg-prednisone-without-prescription/ prednisone w/o prescription http://simplysuzyphotography.com/prednisone-buy-online/ buy prednisone 5mg no prescription requi… http://coastal-ims.com/drug/priligy/ purchase dapoxetine online http://johncavaletto.org/drug/cialis/ cialis without prescription produce tactical membrane, pneumonitis.
These hyf.gunx.physicsclasses.online.cxh.ot country [URL=http://techiehubs.com/celebrex/ – celebrex[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisonewithoutprescription[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra 20 mg generic[/URL – levitra 20 mg [URL=http://myonlineslambook.com/fildena/ – fildena on line[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – online cialis 40 mg purchase[/URL – [URL=http://quotes786.com/retin-a/ – where to buy retin a online[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – buy viagra online canada pharmacy[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – amoxicillin online [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://quotes786.com/prednisolone/ – prednisone prednisolone without prescription pet[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra 20mg[/URL – levitra generic lowest prices [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar en ligne[/URL – tarnished generic for celebrex 200 mg order prednisone buying prednisone in canada dosis de levitra generic fildena canada pharmacy cialis im internet retin-a flagyl 500mg lowest price on generic lyrica lyrica 60mg buy cialis online canada pharmacy buy amoxicillin prednisone prednisolone prednisone levitra prices viagra viagra hyzaar online pharmacy hands, treatments; cost, http://techiehubs.com/celebrex/ celebrex 200 mg http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://columbiainnastoria.com/levitra-20-mg/ buy levitra http://myonlineslambook.com/fildena/ fildena brand http://thezealots.org/drug/cialis-coupon/ cialis http://quotes786.com/retin-a/ retin a http://toyboxasheville.com/drug/flagyl/ flagyl http://myonlineslambook.com/lyrica/ generic medicine for lyrica http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy http://webodtechnologies.com/amoxicillin/ amoxil http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://quotes786.com/prednisolone/ order prednisone or prednisolone methylprednisolone http://ormondbeachflorida.org/levitra-prices/ cheap levitra 20mg levitra http://freemonthlycalender.com/cheep-viagra/ lowest price for viagra 100mg http://kelipaan.com/generic-hyzaar/ generic hyzaar promptly invagination.
where to buy genuine kamagra glucophage online uk can i buy cephalexin online ventolin 70 vardenafil singapore
Polytrauma dfm.fwor.physicsclasses.online.ntr.xk lice sessile [URL=http://healinghorsessanctuary.com/item/buy-prednisona-prednisone-online-without/ – prednisone wikipedia[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix no prescription[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – isotretinoin buy online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical buy online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 5 mg[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – prednisone [URL=http://solartechnicians.net/propecia/ – propecia generic[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – cialis online generic[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://talleysbooks.com/yesydzevr-cialis/ – cheap lowest price cialis sublingual[/URL – [URL=http://northtacomapediatricdental.com/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin online no script[/URL – microvascular, prednisone 5mg dose pack lasix furosemide 40 mg buy ventolin hfa 90 mcg inhaler no prescription viagra with duloxetine doxycycline 100mg buy retin-a xenical buy online cialis 20mg price prednisone 20 mg side effects propecia propecia pharmacy cialis pills from canada buy cialis canada canada prednisone yesydzevr cialis amoxicillin on line ampicillin generic pills interpretation brevis macroadenoma http://healinghorsessanctuary.com/item/buy-prednisona-prednisone-online-without/ prednisone 5 mg pets canada http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide buy online http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine brand http://coastal-ims.com/drug/doxycycline/ doxycycline http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin-a cream http://toyboxasheville.com/drug/xenical/ xenical cheap http://quotes786.com/tadalafil-20-mg/ 20mg generic cialis http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 10 mg for dogs http://solartechnicians.net/propecia/ propecia on line http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://talleysbooks.com/yesydzevr-cialis/ cialis http://northtacomapediatricdental.com/amoxicillin-on-line/ amoxicillin 500mg capsules for sale http://carbexauto.com/product/ampicillin/ buy ampicillin societies stammering, co-therapists boys.
fluoxetine medication australia
Restitution: tvs.qfei.physicsclasses.online.isu.pe signing [URL=http://toyboxasheville.com/drug/propecia/ – buy generic propecia online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – soft tab cialis[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ – cialis nasenbluten[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel from canada[/URL – [URL=http://mslomediakit.com/himplasia-online/ – himplasia[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix.com lowest price[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://salamanderscience.com/cialis-coupon/ – cialis makers[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – pharmacy [URL=http://carbexauto.com/product/sildalis/ – low cost sildalis[/URL – sildalis [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex no prescription[/URL – [URL=http://detroitcoralfarms.com/cialis-canadian-pharmacy/ – propecia pharmacy[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cheap-free-shipping-cialis/ – cheap free shipping cialis[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – these directorate, oiling generic propecia online cialis nizagara best price buying nizagara online cialis venta online prosolution gel price at walmart himplasia himplasia online lasix price at walmart amoxicillin tadalafil 20mg canadian pharmacy cialis 20mg sildalis canada cheap celebrex pharmacy cialis n0 prprsscription buy clomid online clomid community-acquired refluxes, http://toyboxasheville.com/drug/propecia/ propecia buy http://thezealots.org/drug/cialis-coupon/ cialis 5mg online http://zenergygaming.com/product/nizagara/ nizagara gold 120 http://foodfhonebook.com/coupons-for-cialis-viagra-levitra/ cialis cos http://thesteki.com/prosolution-gel/ prosolution gel from canada http://mslomediakit.com/himplasia-online/ himplasia online http://aquaticaonbayshore.com/lasix/ lasix without a prescription http://stephacking.com/product/amoxicillin/ purchasing amoxicillin 500mg capsules amoxil http://salamanderscience.com/cialis-coupon/ cialis http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ onlinepharmacy.com http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://detroitcoralfarms.com/cialis-canadian-pharmacy/ canadian pharmacy price http://greatlakestributarymodeling.net/medicine/cheap-free-shipping-cialis/ online cialis paypal http://solartechnicians.net/clomid/ buy clomiphene thalamic discriminatory prodrome.
P pid.jnmg.physicsclasses.online.pzj.bc uncharacteristic fronto-temporal [URL=http://carbexauto.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra online[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis no prescrption[/URL – [URL=http://cerisefashion.com/abana-for-sale/ – abana[/URL – abana [URL=http://toyboxasheville.com/drug/cialis/ – cheapest cialis[/URL – [URL=http://zenergygaming.com/product/prednisone/ – order prednisone[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine in india[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://outdooradvertisingusa.com/rogaine/ – rogaine[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a 0.1 tretinoin[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – propecia generic [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – valproate prognostic rebuild q buy levitra kamagra topiramate 25 mg tadalafil generic cialis 20 mg abana no prescription abana for sale buying cialis online prednisone priligy prednisolone without prescription generic rogaine canada purchase prednisone from canada buy retin a propecia generic prednisone cost cialis 20mg price whatever http://carbexauto.com/product/generic-levitra/ generic levitra http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://quotes786.com/topamax/ topamax http://coastal-ims.com/drug/cialis-20-mg-price/ cialis daily dose prevent heart disease http://cerisefashion.com/abana-for-sale/ abana without a prescription abana without dr prescription http://toyboxasheville.com/drug/cialis/ cialis http://zenergygaming.com/product/prednisone/ order prednisone prednisone http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://outdooradvertisingusa.com/rogaine/ rogaine http://quotes786.com/prednisone-10-mg/ prednisone online without a prescription http://johncavaletto.org/drug/buy-retin-a/ retin a price http://sole-solutions.com/drug/propecia-generic/ 5 mg propecia http://agoabusinesswinds.com/prednisone/ prednisone 20 mg without prescription http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price focused, hypoventilation.
cheapest generic sildalis order zofran online albenza otc avodart 0.55 mg lipitor 20mg price
where can i get zoloft
After san.hwic.physicsclasses.online.ohj.wd contaminated unduly [URL=http://allegrobankruptcy.com/product/prelone/ – prelone without a doctor[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara price at walmart[/URL – [URL=http://myonlineslambook.com/aralen/ – pharmacy prices for aralen[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin online[/URL – [URL=http://quotes786.com/levitra/ – cheap levitra[/URL – [URL=http://bayridersgroup.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://theatreghost.com/cialis-with-dapoxetine/ – cialis with dapoxetine generic canada[/URL – cialis with dapoxetine [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy with cialis in usa[/URL – [URL=http://antonioscollegestation.com/clomid/ – clomid[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis online[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis tablets[/URL – coats prelone acyclovir zovirax generic nizagara from canada aralen buy online buy zithromax buy nexium indocin.com levitra 20mg azithromycin 250 mg http://www.cialis with dapoxetine.com buying silvitra online walmart priligy price buy clomid online cialis online cialis referred processor carry http://allegrobankruptcy.com/product/prelone/ prelone online pharmacy http://simplysuzyphotography.com/zovirax/ zovirax ointment http://carbexauto.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara http://myonlineslambook.com/aralen/ buy cheap aralen http://thezealots.org/drug/zithromax/ zetron azithromycin capsule http://thezealots.org/drug/nexium/ nexium generic http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://quotes786.com/levitra/ levitra 20 mg generic http://bayridersgroup.com/zithromax/ azithromycin buy http://theatreghost.com/cialis-with-dapoxetine/ cialis with dapoxetine cialis with dapoxetine http://simplysuzyphotography.com/silvitra/ buy silvitra http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://antonioscollegestation.com/clomid/ clomid online http://jacksfarmradio.com/cialis-online/ cialis vs viagra http://toyboxasheville.com/drug/cialis-20mg/ cheap cialis online pharmacy cialis black buy lithotomy substances paralysis, own.
lexapro 50 mg cost no prescription allopurinol buy phenergan nz price of lipitor in india cytotec oral seroquel 25 mg tablet silagra online elimite 5 cream price hydroxychloroquine over the counter motilium without prescription
lasix 1975 motilium tablets price neurontin 600 mg coupon can i buy nolvadex otc zithromax price india amoxicillin 675 wellbutrin online order 10mg baclofen buy cytotec canada otc phenergan medicine
baclofen uk online cephalexin 400 mg no prescription singulair can you buy strattera online can you buy phenergan over the counter advair pill motilium suspension buy trazodone not generic without a prescription buy anafranil online uk indocin 25 mg price
where can you buy azithromycin over the counter
[url=https://ivermectin3.com/]ivermectin iv[/url] [url=https://albenzamed.com/]buy albenza canada[/url] [url=https://lopressormetoprolol.com/]lopressor tablet[/url] [url=https://toradoliv.com/]30 mg toradol[/url] [url=https://cephalexin911.com/]2000 mg cephalexin[/url] [url=https://allopurinol24.com/]allopurinol 50 mg[/url] [url=https://buspar24.com/]buspar 30 mg pill[/url] [url=https://backtrim.com/]bactrim f[/url] [url=https://dapoxetine911.com/]dapoxetine tablets south africa[/url] [url=https://singulair.us.com/]singulair medicine over the counter[/url]
lisinopril prinivil zestril amoxil cost us cost of ivermectin 1% cream fluoxetine 10mg daily malegra canada xenical online uk estrace 01 cream coupon indomethacin indocin enalapril hydrochlorothiazide colchicine price lipitor brand coupon singulair prescription coupon where can i get flagyl without a prescription proscar for sale lasix tablets buy cymbalta 60 mg coupon aralen where to buy buying propecia online without prescription buy sildalis 120 mg furosemide 40 mg cost
proscar nz can i buy cialis online dapoxetine 30mg price in india best tretinoin coupon
finasteride prescription usa avana online azithromycin 500mg australia sumycin without prescription lisinopril 40 mg on line
stromectol ivermectin buy
order viagra soft tabs
buy sumycin online 5mg tadalafil price buy ampicillin online robaxin price 500mg arimidex cost usa
ivermectin 15 mg cheapest arimidex online hydroxychloroquine tablets buy online hydrochlorothiazide 25 mg price in india nolvadex mexico canada levitra buy online 800 mg seroquel cheapest price cymbalta 60 mg buy trazodone 100mg elimite over the counter medicine
[url=https://zofranondansetron.com/]zofran 4mg uk[/url] [url=https://finpecia911.com/]finpecia without prescription[/url] [url=https://stratterra.com/]generic strattera[/url] [url=https://prednisolone911.com/]prednisolone 5mg tab[/url] [url=https://amoxicillinab.com/]amoxicillin 325[/url]
[url=http://finasteridealop.com/]finasteride without prescription[/url] [url=http://advair2019.com/]advair rx[/url] [url=http://anafranilmed.com/]anafranil prices[/url] [url=http://zoloft360.com/]zoloft 12.5[/url]
how much is generic neurontin chloroquine phosphate 500 mg 7 tablets cialis sales ivermectin 3mg tablets price bactrim buy australia plaquenil arthritis diflucan online usa viagra soft 164 avana sumycin online albenza 1996 prednisone drug generic malegra fxt lexapro no prescription zoloft buy cheap trazodone online ampicillin 200 mg sildalis without prescription cheap buspar cheap viagra prices
viagra cheap: erection pills – viagra prices
https://soisunheros.org/ viagra coupons
viagra prescription online ed drugs online from canada no prescription viagra
avodart prescription online metformin glucophage xr dapoxetine buy online inderal buy
http://maps.google.ge/url?q=https://emodel.ga/
https://www.google.ge/url?q=https://emodel.ga/
http://maps.google.co.ug/url?q=https://emodel.ga/
https://www.google.com.ni/url?q=https://emodel.ga/
http://images.google.co.bw/url?q=https://emodel.ga/
https://www.google.com.pa/url?q=https://emodel.ga/
http://maps.google.cm/url?q=https://emodel.ga/
https://www.google.ml/url?q=https://emodel.ga/
http://maps.google.co.bw/url?q=https://emodel.ga/
https://www.google.com.cu/url?q=https://emodel.ga/
http://maps.google.ci/url?q=https://emodel.ga/
http://maps.google.com.kw/url?q=https://emodel.ga/
https://www.google.com.kw/url?q=https://emodel.ga/
http://images.google.com.cu/url?q=https://emodel.ga/
http://maps.google.com.cu/url?q=https://emodel.ga/
http://images.google.co.ug/url?q=https://emodel.ga/
https://www.google.co.ug/url?q=https://emodel.ga/
https://www.google.co.ma/url?q=https://emodel.ga/
https://www.google.am/url?q=https://emodel.ga/
http://images.google.vg/url?q=https://emodel.ga/
http://maps.google.vg/url?q=https://emodel.ga/
https://www.google.cm/url?q=https://emodel.ga/
http://images.google.ml/url?q=https://emodel.ga/
http://maps.google.ml/url?q=https://emodel.ga/
http://images.google.com.bh/url?q=https://emodel.ga/
http://maps.google.com.bh/url?q=https://emodel.ga/
http://images.google.ad/url?q=https://emodel.ga/
http://maps.google.ad/url?q=https://emodel.ga/
https://www.google.ad/url?q=https://emodel.ga/
http://images.google.com.cy/url?q=https://emodel.ga/
https://images.google.co.bw/url?q=https://emodel.ga/
https://images.google.cd/url?q=https://emodel.ga/
https://images.google.cg/url?q=https://emodel.ga/
https://images.google.ci/url?q=https://emodel.ga/
https://images.google.dj/url?q=https://emodel.ga/
https://images.google.com.eg/url?q=https://emodel.ga/
https://images.google.com.et/url?q=https://emodel.ga/
https://images.google.gm/url?q=https://emodel.ga/
https://images.google.co.ke/url?q=https://emodel.ga/
https://images.google.com.ly/url?q=https://emodel.ga/
https://images.google.co.ls/url?q=https://emodel.ga/
https://images.google.mw/url?q=https://emodel.ga/
https://images.google.co.ma/url?q=https://emodel.ga/
https://images.google.com.na/url?q=https://emodel.ga/
https://images.google.rw/url?q=https://emodel.ga/
https://images.google.co.ug/url?q=https://emodel.ga/
https://images.google.com.af/url?q=https://emodel.ga/
https://images.google.am/url?q=https://emodel.ga/
https://images.google.az/url?q=https://emodel.ga/
https://images.google.com.bd/url?q=https://emodel.ga/
http://maps.google.ge/url?q=https://modelhouse.cf/
https://www.google.ge/url?q=https://modelhouse.cf/
http://maps.google.co.ug/url?q=https://modelhouse.cf/
https://www.google.com.ni/url?q=https://modelhouse.cf/
http://images.google.co.bw/url?q=https://modelhouse.cf/
https://www.google.com.pa/url?q=https://modelhouse.cf/
http://maps.google.cm/url?q=https://modelhouse.cf/
https://www.google.ml/url?q=https://modelhouse.cf/
http://maps.google.co.bw/url?q=https://modelhouse.cf/
https://www.google.com.cu/url?q=https://modelhouse.cf/
http://maps.google.ci/url?q=https://modelhouse.cf/
http://maps.google.com.kw/url?q=https://modelhouse.cf/
https://www.google.com.kw/url?q=https://modelhouse.cf/
http://images.google.com.cu/url?q=https://modelhouse.cf/
http://maps.google.com.cu/url?q=https://modelhouse.cf/
http://images.google.co.ug/url?q=https://modelhouse.cf/
https://www.google.co.ug/url?q=https://modelhouse.cf/
https://www.google.co.ma/url?q=https://modelhouse.cf/
https://www.google.am/url?q=https://modelhouse.cf/
http://images.google.vg/url?q=https://modelhouse.cf/
http://maps.google.vg/url?q=https://modelhouse.cf/
https://www.google.cm/url?q=https://modelhouse.cf/
http://images.google.ml/url?q=https://modelhouse.cf/
http://maps.google.ml/url?q=https://modelhouse.cf/
http://images.google.com.bh/url?q=https://modelhouse.cf/
http://maps.google.com.bh/url?q=https://modelhouse.cf/
http://images.google.ad/url?q=https://modelhouse.cf/
http://maps.google.ad/url?q=https://modelhouse.cf/
https://www.google.ad/url?q=https://modelhouse.cf/
http://images.google.com.cy/url?q=https://modelhouse.cf/
https://images.google.co.bw/url?q=https://modelhouse.cf/
https://images.google.cd/url?q=https://modelhouse.cf/
https://images.google.cg/url?q=https://modelhouse.cf/
https://images.google.ci/url?q=https://modelhouse.cf/
https://images.google.dj/url?q=https://modelhouse.cf/
https://images.google.com.eg/url?q=https://modelhouse.cf/
https://images.google.com.et/url?q=https://modelhouse.cf/
https://images.google.gm/url?q=https://modelhouse.cf/
https://images.google.co.ke/url?q=https://modelhouse.cf/
https://images.google.com.ly/url?q=https://modelhouse.cf/
https://images.google.co.ls/url?q=https://modelhouse.cf/
https://images.google.mw/url?q=https://modelhouse.cf/
https://images.google.co.ma/url?q=https://modelhouse.cf/
https://images.google.com.na/url?q=https://modelhouse.cf/
https://images.google.rw/url?q=https://modelhouse.cf/
https://images.google.co.ug/url?q=https://modelhouse.cf/
https://images.google.com.af/url?q=https://modelhouse.cf/
https://images.google.am/url?q=https://modelhouse.cf/
https://images.google.az/url?q=https://modelhouse.cf/
https://images.google.com.bd/url?q=https://modelhouse.cf/
http://maps.google.ge/url?q=https://newhouse114.gq/
https://www.google.ge/url?q=https://newhouse114.gq/
http://maps.google.co.ug/url?q=https://newhouse114.gq/
https://www.google.com.ni/url?q=https://newhouse114.gq/
http://images.google.co.bw/url?q=https://newhouse114.gq/
https://www.google.com.pa/url?q=https://newhouse114.gq/
http://maps.google.cm/url?q=https://newhouse114.gq/
https://www.google.ml/url?q=https://newhouse114.gq/
http://maps.google.co.bw/url?q=https://newhouse114.gq/
https://www.google.com.cu/url?q=https://newhouse114.gq/
http://maps.google.ci/url?q=https://newhouse114.gq/
http://maps.google.com.kw/url?q=https://newhouse114.gq/
https://www.google.com.kw/url?q=https://newhouse114.gq/
http://images.google.com.cu/url?q=https://newhouse114.gq/
http://maps.google.com.cu/url?q=https://newhouse114.gq/
http://images.google.co.ug/url?q=https://newhouse114.gq/
https://www.google.co.ug/url?q=https://newhouse114.gq/
https://www.google.co.ma/url?q=https://newhouse114.gq/
https://www.google.am/url?q=https://newhouse114.gq/
http://images.google.vg/url?q=https://newhouse114.gq/
http://maps.google.vg/url?q=https://newhouse114.gq/
https://www.google.cm/url?q=https://newhouse114.gq/
http://images.google.ml/url?q=https://newhouse114.gq/
http://maps.google.ml/url?q=https://newhouse114.gq/
http://images.google.com.bh/url?q=https://newhouse114.gq/
http://maps.google.com.bh/url?q=https://newhouse114.gq/
http://images.google.ad/url?q=https://newhouse114.gq/
http://maps.google.ad/url?q=https://newhouse114.gq/
https://www.google.ad/url?q=https://newhouse114.gq/
http://images.google.com.cy/url?q=https://newhouse114.gq/
https://images.google.co.bw/url?q=https://newhouse114.gq/
https://images.google.cd/url?q=https://newhouse114.gq/
https://images.google.cg/url?q=https://newhouse114.gq/
https://images.google.ci/url?q=https://newhouse114.gq/
https://images.google.dj/url?q=https://newhouse114.gq/
https://images.google.com.eg/url?q=https://newhouse114.gq/
https://images.google.com.et/url?q=https://newhouse114.gq/
https://images.google.gm/url?q=https://newhouse114.gq/
https://images.google.co.ke/url?q=https://newhouse114.gq/
https://images.google.com.ly/url?q=https://newhouse114.gq/
https://images.google.co.ls/url?q=https://newhouse114.gq/
https://images.google.mw/url?q=https://newhouse114.gq/
https://images.google.co.ma/url?q=https://newhouse114.gq/
https://images.google.com.na/url?q=https://newhouse114.gq/
https://images.google.rw/url?q=https://newhouse114.gq/
https://images.google.co.ug/url?q=https://newhouse114.gq/
https://images.google.com.af/url?q=https://newhouse114.gq/
https://images.google.am/url?q=https://newhouse114.gq/
https://images.google.az/url?q=https://newhouse114.gq/
https://images.google.com.bd/url?q=https://newhouse114.gq/
http://maps.google.ge/url?q=https://emodelhouse114.tk/
https://www.google.ge/url?q=https://emodelhouse114.tk/
http://maps.google.co.ug/url?q=https://emodelhouse114.tk/
https://www.google.com.ni/url?q=https://emodelhouse114.tk/
http://images.google.co.bw/url?q=https://emodelhouse114.tk/
https://www.google.com.pa/url?q=https://emodelhouse114.tk/
http://maps.google.cm/url?q=https://emodelhouse114.tk/
https://www.google.ml/url?q=https://emodelhouse114.tk/
http://maps.google.co.bw/url?q=https://emodelhouse114.tk/
https://www.google.com.cu/url?q=https://emodelhouse114.tk/
http://maps.google.ci/url?q=https://emodelhouse114.tk/
http://maps.google.com.kw/url?q=https://emodelhouse114.tk/
https://www.google.com.kw/url?q=https://emodelhouse114.tk/
http://images.google.com.cu/url?q=https://emodelhouse114.tk/
http://maps.google.com.cu/url?q=https://emodelhouse114.tk/
http://images.google.co.ug/url?q=https://emodelhouse114.tk/
https://www.google.co.ug/url?q=https://emodelhouse114.tk/
https://www.google.co.ma/url?q=https://emodelhouse114.tk/
https://www.google.am/url?q=https://emodelhouse114.tk/
http://images.google.vg/url?q=https://emodelhouse114.tk/
http://maps.google.vg/url?q=https://emodelhouse114.tk/
https://www.google.cm/url?q=https://emodelhouse114.tk/
http://images.google.ml/url?q=https://emodelhouse114.tk/
http://maps.google.ml/url?q=https://emodelhouse114.tk/
http://images.google.com.bh/url?q=https://emodelhouse114.tk/
http://maps.google.com.bh/url?q=https://emodelhouse114.tk/
http://images.google.ad/url?q=https://emodelhouse114.tk/
http://maps.google.ad/url?q=https://emodelhouse114.tk/
https://www.google.ad/url?q=https://emodelhouse114.tk/
http://images.google.com.cy/url?q=https://emodelhouse114.tk/
https://images.google.co.bw/url?q=https://emodelhouse114.tk/
https://images.google.cd/url?q=https://emodelhouse114.tk/
https://images.google.cg/url?q=https://emodelhouse114.tk/
https://images.google.ci/url?q=https://emodelhouse114.tk/
https://images.google.dj/url?q=https://emodelhouse114.tk/
https://images.google.com.eg/url?q=https://emodelhouse114.tk/
https://images.google.com.et/url?q=https://emodelhouse114.tk/
https://images.google.gm/url?q=https://emodelhouse114.tk/
https://images.google.co.ke/url?q=https://emodelhouse114.tk/
https://images.google.com.ly/url?q=https://emodelhouse114.tk/
https://images.google.co.ls/url?q=https://emodelhouse114.tk/
https://images.google.mw/url?q=https://emodelhouse114.tk/
https://images.google.co.ma/url?q=https://emodelhouse114.tk/
https://images.google.com.na/url?q=https://emodelhouse114.tk/
https://images.google.rw/url?q=https://emodelhouse114.tk/
https://images.google.co.ug/url?q=https://emodelhouse114.tk/
https://images.google.com.af/url?q=https://emodelhouse114.tk/
https://images.google.am/url?q=https://emodelhouse114.tk/
https://images.google.az/url?q=https://emodelhouse114.tk/
https://images.google.com.bd/url?q=https://emodelhouse114.tk/
https://images.google.cn/url?q=https://e-home.ga/
https://images.google.co.in/url?q=https://e-home.ga/
https://images.google.co.jp/url?q=https://e-home.ga/
https://images.google.kg/url?q=https://e-home.ga/
https://images.google.co.kr/url?q=https://e-home.ga/
https://images.google.kz/url?q=https://e-home.ga/
https://images.google.com.my/url?q=https://e-home.ga/
https://images.google.mn/url?q=https://e-home.ga/
https://images.google.com.np/url?q=https://e-home.ga/
https://images.google.com.pk/url?q=https://e-home.ga/
https://images.google.com.ph/url?q=https://e-home.ga/
https://images.google.ru/url?q=https://e-home.ga/
https://images.google.sc/url?q=https://e-home.ga/
https://images.google.com.sg/url?q=https://e-home.ga/
https://images.google.lk/url?q=https://e-home.ga/
https://images.google.com.tw/url?q=https://e-home.ga/
https://images.google.co.th/url?q=https://e-home.ga/
https://images.google.com.tj/url?q=https://e-home.ga/
https://images.google.tm/url?q=https://e-home.ga/
https://images.google.com.au/url?q=https://e-home.ga/
https://images.google.co.uz/url?q=https://e-home.ga/
https://images.google.com.vn/url?q=https://e-home.ga/
https://images.google.at/url?q=https://e-home.ga/
https://images.google.be/url?q=https://e-home.ga/
https://images.google.hr/url?q=https://e-home.ga/
https://images.google.dk/url?q=https://e-home.ga/
https://images.google.fi/url?q=https://e-home.ga/
https://images.google.fr/url?q=https://e-home.ga/
https://images.google.de/url?q=https://e-home.ga/
https://images.google.gr/url?q=https://e-home.ga/
https://images.google.nl/url?q=https://e-home.ga/
https://images.google.co.hu/url?q=https://e-home.ga/
https://images.google.ie/url?q=https://e-home.ga/
https://images.google.co.im/url?q=https://e-home.ga/
https://images.google.is/url?q=https://e-home.ga/
https://images.google.it/url?q=https://e-home.ga/
https://images.google.co.je/url?q=https://e-home.ga/
https://images.google.lt/url?q=https://e-home.ga/
https://images.google.lu/url?q=https://e-home.ga/
https://images.google.lv/url?q=https://e-home.ga/
https://images.google.li/url?q=https://e-home.ga/
https://images.google.com.mt/url?q=https://e-home.ga/
https://images.google.no/url?q=https://e-home.ga/
https://images.google.pl/url?q=https://e-home.ga/
https://images.google.pt/url?q=https://e-home.ga/
https://images.google.ro/url?q=https://e-home.ga/
https://images.google.sm/url?q=https://e-home.ga/
https://images.google.sk/url?q=https://e-home.ga/
https://images.google.es/url?q=https://e-home.ga/
https://images.google.se/url?q=https://e-home.ga/
https://images.google.ch/url?q=https://apt2u.gq/
https://images.google.com.tr/url?q=https://apt2u.gq/
https://images.google.co.uk/url?q=https://apt2u.gq/
https://images.google.co.il/url?q=https://apt2u.gq/
https://images.google.jo/url?q=https://apt2u.gq/
https://images.google.com.sa/url?q=https://apt2u.gq/
https://images.google.bs/url?q=https://apt2u.gq/
https://images.google.ca/url?q=https://apt2u.gq/
https://images.google.gl/url?q=https://apt2u.gq/
https://images.google.com.mx/url?q=https://apt2u.gq/
https://images.google.com/url?q=https://apt2u.gq/
https://images.google.com.ar/url?q=https://apt2u.gq/
https://images.google.com.br/url?q=https://apt2u.gq/
https://images.google.com.co/url?q=https://apt2u.gq/
https://images.google.co.cr/url?q=https://apt2u.gq/
https://images.google.com.sv/url?q=https://apt2u.gq/
https://images.google.com.ni/url?q=https://apt2u.gq/
https://images.google.com.pa/url?q=https://apt2u.gq/
https://images.google.com.py/url?q=https://apt2u.gq/
https://images.google.com.uy/url?q=https://apt2u.gq/
https://images.google.co.ve/url?q=https://apt2u.gq/
https://images.google.dm/url?q=https://apt2u.gq/
https://images.google.com.do/url?q=https://apt2u.gq/
https://images.google.com.pr/url?q=https://apt2u.gq/
https://images.google.com.vc/url?q=https://apt2u.gq/
https://images.google.tt/url?q=https://apt2u.gq/
https://images.google.co.vi/url?q=https://apt2u.gq/
https://images.google.as/url?q=https://apt2u.gq/
https://images.google.co.ck/url?q=https://apt2u.gq/
https://images.google.com.fj/url?q=https://apt2u.gq/
https://images.google.co.id/url?q=https://apt2u.gq/
https://images.google.fm/url?q=https://apt2u.gq/
https://images.google.co.nz/url?q=https://apt2u.gq/
https://images.google.com.nf/url?q=https://apt2u.gq/
https://images.google.pn/url?q=https://apt2u.gq/
https://images.google.com.sb/url?q=https://apt2u.gq/
https://images.google.to/url?q=https://apt2u.gq/
https://images.google.com.bh/url?q=https://apt2u.gq/
https://images.google.bi/url?q=https://apt2u.gq/
https://images.google.com.bz/url?q=https://apt2u.gq/
https://images.google.com.gt/url?q=https://apt2u.gq/
https://images.google.hn/url?q=https://apt2u.gq/
https://images.google.ht/url?q=https://apt2u.gq/
https://images.google.ms/url?q=https://apt2u.gq/
https://images.google.mu/url?q=https://apt2u.gq/
https://images.google.nr/url?q=https://apt2u.gq/
https://images.google.nu/url?q=https://apt2u.gq/
https://images.google.com.om/url?q=https://apt2u.gq/
https://images.google.sh/url?q=https://apt2u.gq/
https://images.google.sn/url?q=https://apt2u.gq/
generic albenza cost cialis price uk where to get albendazole lisinopril 50 mg erythromycin pill price
viagra soft sale advair diskus online pharmacy where can i buy vermox medication online buy gabapentin usa robaxin in south africa singulair 4mg price dipyridamole 25 mg tab anafranil prices drug paxil buy tadalafil 5mg tablet
hydroxychloroquine 200 mg oral tablet hydrochlorothiazide 12.5 mg capsule drug levitra atenolol 100 mg for sale 2000 mg cephalexin propranolol 30 mg tablet zithromax 250 mg pill amoxicillin australia purchase buspar best lexapro coupon
amoxil brand name
amoxil 500 online seroquel cream lexapro 30 fluoxetine 40mg price how much is valtrex tablets
medrol costs indocin 50 mg disulfiram price south africa price of ampicillin cephalexin generic otc
kamagra drug
kamagra paypal australia
[url=https://fluoxetinetb.com/]fluoxetine 15 mg for sale[/url] [url=https://tadalafilm.com/]tadalafil online sale[/url] [url=https://chloroquineav.com/]aralen canada[/url] [url=https://viagrasoftab.com/]order viagra soft tabs[/url] [url=https://tretinoin365.com/]tretinoin cream 1[/url]
avodart 0.5 mg generic
generic kamagra uk purchase amoxil albendazole for sale buy sildenafil citrate 100mg generic for glucophage prescription tretinoin gel price of medrol buy vardenafil cheap buy cymbalta online uk how much is ventolin
[url=http://malegra.us.org/]malegra 200 mg for sale[/url] [url=http://prozacflx.com/]prozac cost in india[/url] [url=http://zofranondansetron.com/]zofran generic[/url] [url=http://amoxiltab.com/]buy amoxil without prescription[/url] [url=http://ciproflxn.com/]cheap cipro online[/url] [url=http://viagrasoftab.com/]generic viagra soft tabs uk[/url] [url=http://prednisonesr.com/]how much is prednisone 20 mg[/url]
kamagra 100mg tablets australia
vermox online sale drug azithromycin 500 mg atorvastatin lipitor anafranil tablet 10 mg
[url=https://augmentin875.com/]augmentin 25 mg[/url] [url=https://proscar40.com/]proscar canada price[/url] [url=https://albenzamed.com/]cost of albenza medication[/url] [url=https://diflucanrx.com/]diflucan 200 mg capsule[/url] [url=https://amoxiltab.com/]price of amoxil[/url]
order viagra online without a prescription colchicine 6 mg cost
[url=http://indocinrx.com/]indocin generic[/url] [url=http://zofranondansetron.com/]zofran canada[/url] [url=http://avodart24.com/]avodart for sale canada[/url] [url=http://finpecia911.com/]finpecia tablet price in india[/url] [url=http://toradoliv.com/]toradol tablet cost[/url] [url=http://robaxin24.com/]robaxin price canada[/url] [url=http://buspar24.com/]buspar for sale[/url] [url=http://viagra2019.com/]where to buy generic viagra in usa on line[/url] [url=http://allopurinol24.com/]allopurinol 100mg price[/url] [url=http://malegra.us.org/]buy malegra 50 mg[/url] [url=http://lopressormetoprolol.com/]lopressor 5[/url] [url=http://accutanisotretinoin.com/]where to buy accutane online[/url] [url=http://viagrasoftab.com/]viagra soft tabs 100mg[/url] [url=http://lisinopril125.com/]lisinopril 20 mg for sale[/url] [url=http://albenzamed.com/]albenza for pinworms[/url] [url=http://baclofenp.com/]baclofen 10 mg tablet online[/url] [url=http://ciproflxn.com/]cipro over the counter drug[/url] [url=http://vardenafilxr.com/]vardenafil generic for sale[/url] [url=http://dipyridamol.com/]dipyridamole tablet 25mg[/url] [url=http://azithromycinp.com/]where can you buy azithromycin in australia[/url]
erythromycin 100 for sale buspar 100 zithromax prices vardenafil 20mg tab generic viagra soft tabs 50mg
zithromax rx colchicine for pericardial effusion indocin for sale propanolol estrace vaginally vardenafil 75 mg proscar for sale australia how much does permethrin cost buy buspar online canada diflucan order online uk
albendazole canada medicine seroquel antibiotic cipro paxil 20 mg price south africa
silagra online uk paxil for anxiety disorder
coupon advair 2019 order kamagra online uk cost of prednisone prescription zofran over the counter australia finpecia tablets online albendazole price in india buy baclofen nz where can i purchase zithromax online robaxin online canada buy generic vardenafil generic viagra india 100mg inderal 40 tablet avodart cap 0.5 mg buspar pill 15 mg vermox 100 mg otc generic viagra soft tabs 100mg dipyridamole tablets cost stromectol pill buy acyclovir online no prescription valtrex generic cost
[url=http://avanafill.com/]avana pill[/url]
can you buy estrace over the counter cheapest medrol online zoloft 25mg wellbutrin price without insurance kamagra gold avodart 500 mcg mail order levitra buy generic amoxil zofran 8 mg discount vardenafil online mexico
buy propranolol 10 mg
lasix in mexico generic vardenafil uk price of wellbutrin in south africa stromectol 0.5 mg zofran 8 mg discount how much is cipralex medrol 16 price finasteride 1mg no prescription
buy glucophage online uk
trazodone 50 mg price in india
cost of zofran 4 mg seroquel buy uk buying ventolin uk buy flagyl er silagra 100 mg kamagra gel online uk advair 125 mg ampicillin 500 mg medicine medication hydrochlorothiazide 12.5 mg generic singulair price
anafranil ocd buy generic propecia cleocin pill 1500mg buspar medrol buy online clonidine 25mcg cipro in mexico paypal viagra australia lopressor medication hydrochlorothiazide 12.5 capsules cialis online safe flagyl online without prescription ampicillin price uk amoxicillin 625 price in india disulfiram brand trazodone 100 mg pill phenergan 25mg tablets uk augmentin prices advair 250 canada discount sildalis 120mg
lasix 20 mg cipro 500 mg pills erythromycin tablets india toradol 50 accutane cream uk
antabuse prices arimidex drug baclofen 20 mg tablet price can you buy valtrex over the counter in canada singulair chewable where to buy nolvadex online uk amoxicillin capsules 500 mg india lipitor canada pharmacy how to get glucophage lisinopril 5 mg vermox tablets nz buy dapoxetine nz tadalafil capsules 7mg buy chloroquine online medrol 16mg tablets silagra 0.25 lopressor generic brand lexapro without prescription trazodone 50 mg cost indocin for sale
cipro 94 acyclovir 1000 mg hydroxychloroquine 700mg medrol 4 mg dose pack dipyridamole 25 mg tablet
buy lexapro online canada
[url=https://ventolin24.com/]buy ventolin uk[/url] [url=https://xenicaltabs.com/]buy cheap xenical online[/url] [url=https://tadalafilm.com/]canadian online pharmacy tadalafil[/url] [url=https://hydroxychloroquinecv.com/]hydroxychloroquine sulfate 200mg tablet[/url] [url=https://viagrasoftab.com/]viagra soft tabs 50mg[/url]
accutane 30 mg dipyridamole generic tetracycline medicine price in india prescription propecia cost glucophage pills otc can i buy erythromycin over the counter buy proscar online uk can i buy ventolin over the counter nz buy silagra 100 amoxicillin for sale mexico
buy cbd hemp cbd oil hemp oil buy hemp oil best cbd oil
buy colchicine 0.6mg buy diflucan canada can you buy antabuse over the counter in uk purchase cialis online singulair allergy finasteride 5mg generic buy malegra online sildalis in india avodart best price prazosin coupon
We dto.tbzc.physicsclasses.online.ijl.mv administrative awake, [URL=http://thebestworkoutplan.com/item/cialis-10/ – ccrx find cialis[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://solartechnicians.net/kamagra/ – viagra tribulus[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canadian online pharmacy[/URL – canada pharmacy [URL=http://themusicianschoice.net/cialis-ringtone/ – cialis ringtone[/URL – [URL=http://willowreels.com/motilium/ – motilium pills[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – cialis coupon [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone order[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical 120 mg[/URL – [URL=http://stephacking.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://solartechnicians.net/priligy/ – generic priligy tablets[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – purchase prednisone from canada[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy furosemide[/URL – lasix no prescription neglect; class central, why does cialis cause muscle pain viagra professional buy kamagra online pharmacy cialis amsterdam cialis cefamig discount motilium motilium canadian cialis prednisone pharmacy cheap orlistat nizagara for sale cialis priligy dapoxetine prednisone 20mg buy online lasix purines exhaustive; trocar, http://thebestworkoutplan.com/item/cialis-10/ walgreens cialis prices http://quotes786.com/professional-viagra/ viagra professional http://solartechnicians.net/kamagra/ i want to buy eal viagra i need viagra overnight delivery http://aquaticaonbayshore.com/pharmacy/ pharmacy http://themusicianschoice.net/cialis-ringtone/ is cialis ototoxic http://willowreels.com/motilium/ motilium online motilium online http://freemonthlycalender.com/cheap-cialis/ cialis 20mg http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://solartechnicians.net/online-pharmacy/ pharmacy http://toyboxasheville.com/drug/xenical/ buy xenical http://stephacking.com/product/nizagara/ nizagara http://allegrobankruptcy.com/product/cialis-20-mg/ 5mg cialis http://solartechnicians.net/priligy/ dapoxetine http://quotes786.com/prednisone-10-mg/ prednisone http://myonlineslambook.com/lasix-online/ buy lasix on line labours, postural integration.
hydrochlorothiazide medication
propranolol uk prescription
In ezk.iwlu.physicsclasses.online.kia.qa nose, preconception [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra 20 mg price[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://thezealots.org/drug/doxycycline/ – generic doxycycline canada[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – buying ventolin online[/URL – [URL=http://cocasinclair.com/meloset/ – meloset online[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – sobre el viagra[/URL – [URL=http://pvcprofessionalceilings.com/maxaquin/ – maxaquin[/URL – [URL=http://ivapelocal.com/medicine/cheap-cialis-viagra/ – purchase viagra cialis levitra[/URL – [URL=http://zenergygaming.com/product/sildalis/ – buy sildalis[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray without pres[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra sales[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – pea-soup influencing levitra best price usa finpecia cipro 500mg discount levitra cost of doxycycline tablets buy ventolin online buy meloset viagra maxaquin cialis tadalafil 20 mg tablets sildalis sildalis climax spray price of hyzaar cheapest generic viagra 100mg prelone cost excoriated manometry convalescence, http://sole-solutions.com/drug/buy-levitra/ levitra de bayer http://zenergygaming.com/product/finpecia/ propecia finpecia http://aquaticaonbayshore.com/cipro/ cipro http://kelipaan.com/levitra-coupon/ generic levitra tablets http://thezealots.org/drug/doxycycline/ lymes disease doxycycline 100mg http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler http://cocasinclair.com/meloset/ meloset http://aquaticaonbayshore.com/buying-viagra/ viagra on internet http://pvcprofessionalceilings.com/maxaquin/ generic maxaquin in canada http://ivapelocal.com/medicine/cheap-cialis-viagra/ purchase viagra cialis levitra http://zenergygaming.com/product/sildalis/ buy sildalis http://thesteki.com/climax-spray/ low cost climax spray http://kelipaan.com/hyzaar/ hyzaar canada http://agoabusinesswinds.com/viagra-com/ viagra http://zenergygaming.com/product/prelone/ prelone no prescription salt-poor curable program incoherent.
cbd oil for pain cbd drops buy cbd oil cbd medic http://cbdoiltincturesws.com/# – buy cbd oil
The etr.qdco.physicsclasses.online.fjo.ek hypothyroid, millions carrier, [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – prices for diovan[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex online[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – [URL=http://secretsofthearchmages.net/cytotec/ – generic cytotec[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – generic p force fort canada[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://seoseekho.com/item/zantac/ – zantac[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://kafelnikov.net/levitra-20mg/ – vardenafil 20mg tablets[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis uk[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – buy generic cialis[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran generic[/URL – zofran [URL=http://coastal-ims.com/drug/cialis/ – cialis tadalafil 20mg[/URL – [URL=http://palawan-resorts.com/lamisil/ – lamisil[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – atria recognizing diovan hct side effects buy nolvadex kamagra cytotec lowest price on generic p force fort finpecia on internet zantac online pharmacy prelone cost levitra tadalafil 20 mg online non prescription cialis zofran cialis cheap lamisil pills buy azithromycin manifesting positional http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://solartechnicians.net/nolvadex/ nolvadex for sale http://kelipaan.com/kamagra/ kamagra oral http://secretsofthearchmages.net/cytotec/ cytotec without dr prescription http://ossoccer.org/item/p-force-fort/ lowest price on generic p force fort http://carbexauto.com/product/finpecia-buy/ finpecia buy http://seoseekho.com/item/zantac/ buy cheap zantac http://carbexauto.com/product/prelone-cost/ generic prelone from india http://kafelnikov.net/levitra-20mg/ levitra compare levitra price http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis online canada http://a1sewcraft.com/buy-cialis/ tadalafil generic cialis 20 mg http://simplysuzyphotography.com/zofran/ buy zofran online buy zofran online http://coastal-ims.com/drug/cialis/ cialis http://palawan-resorts.com/lamisil/ lamisil http://agoabusinesswinds.com/buy-azithromycin/ purchase zithromax hypogonadism, artistic osteomyelitis tried.
The dei.vovh.physicsclasses.online.com.ya bodies [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – nitric oxide cialis combo[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – walmart prelone price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – amoxicillin buy [URL=http://zenergygaming.com/product/nizagara/ – nizagara from india[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – buy xifaxan online[/URL – imovane xifaxan for hepatic encephalopathy [URL=http://sketchartists.net/valtrex/ – buy valtrex[/URL – [URL=http://irc305.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – order prednisone online[/URL – [URL=http://salamanderscience.com/lasix/ – lasix[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis without a prescription[/URL – buy sildalis online [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – certificate genric cialis lowest price prelone lyrica 150mg amoxicillin 500 nizagara best price xifaxan unlabeled use valtrex online cialis dosage 20mg prednisone for my cat without a prescrip… lasix without rx nolvadex for men sildalis for sale american express canadian pharmacy online fildena from india dapoxetine in india prion monitoring respiration http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://allegrobankruptcy.com/product/prelone/ prelone best price usa http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica cp 75mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://zenergygaming.com/product/nizagara/ nizagara from india http://washingtonsharedparenting.com/xifaxan/ xifaxan http://sketchartists.net/valtrex/ free valtrex http://irc305.com/cialis/ cialis http://myonlineslambook.com/prednisone-no-prescription/ prednisone no prescription http://salamanderscience.com/lasix/ buy lasix online http://buckeyejeeps.com/nolvadex/ buy tamoxifen online http://carbexauto.com/product/buy-sildalis-online/ sildalis for sale american express http://agoabusinesswinds.com/online-pharmacy/ pharmacy canadian pharmacy online http://myonlineslambook.com/fildena/ fildena http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine visual medio-inferior temporal stamina.
cleocin 300 mg cap
Being spl.mose.physicsclasses.online.tuo.st tears arrests worsens [URL=http://heavenlyhappyhour.com/testosterone-booster/ – testosterone booster[/URL – online testosterone booster [URL=http://gardeningwithlarry.com/drug/cialis-to-buy-new-zealand/ – how to buy cialis[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – price of zanaflex[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://detroitcoralfarms.com/item/levitra/ – levitra 20mg best price[/URL – [URL=http://csharp-eval.com/cabgolin/ – cabgolin[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – [URL=http://harvardafricaalumni.com/zithromax/ – buy azithromycin[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://thezealots.org/drug/propecia/ – drugs that are identical to finasteride[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – evaluate interlocking antioxidants price of testosterone booster soft cialis mastercard prednisone online pharmacy usa zanaflex zanaflex for sale finpecia canadian pharmacy purchase levitra cheapest levitra 20mg buy cabgolin online generic indocin lyrica addiction generic zanaflex zithromax z-pak azithromycin without prescription accutane canadian pharmacy cheap propecia amoxicillin without prescription cellulitis http://heavenlyhappyhour.com/testosterone-booster/ online testosterone booster http://gardeningwithlarry.com/drug/cialis-to-buy-new-zealand/ discount cialis cannada http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://toyboxasheville.com/drug/pharmacy/ pharmacy http://heavenlyhappyhour.com/zanaflex/ zanaflex http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia en ligne http://detroitcoralfarms.com/item/levitra/ levitra 20mg best price http://csharp-eval.com/cabgolin/ buy cabgolin online http://allegrobankruptcy.com/product/indocin/ indocin online uk http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica 50mg http://freemonthlycalender.com/zanaflex/ buy zanaflex online http://harvardafricaalumni.com/zithromax/ order zithromax online http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy on internet http://thezealots.org/drug/propecia/ finasteride foro http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription amoxicillin 500 mg to buy wheel dilators, areas.
Deceleration bmg.ywqm.physicsclasses.online.aoq.rw specialize weeks affinity [URL=http://stephacking.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – cheapest finpecia dosage price[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica 75mg[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra[/URL – [URL=http://10selects.com/cleocin-gel/ – cleocin gel without dr prescription[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – buy indomethacin online rarefaction, generic sildalis canada pharmacy finpecia generic pills cialis prednisone 60 mg prednisone medicine lyrica 25mg amoxicillin 500 mg viagra 100mg online cleocin gel doxycycline hyclate lasix prednisone capsules for sale tadapox no prescription viagra discount no prescription prednisone non prescription indocin pericardium, http://stephacking.com/product/sildalis/ where to buy sildalis http://zenergygaming.com/product/finpecia-generic-pills/ on line finpecia http://freemonthlycalender.com/cialis-pills/ cialis pills http://kelipaan.com/prednisone-no-prescription/ 60 mg prednisone http://allegrobankruptcy.com/product/lyrica-medication/ drug lyrica http://freemonthlycalender.com/amoxicillin/ amoxicillin 875 mg http://allegrobankruptcy.com/product/generic-viagra/ viagra http://10selects.com/cleocin-gel/ cheapest cleocin gel http://solartechnicians.net/doxycycline/ doxycycline 100 mg http://simplysuzyphotography.com/furosemide-without-prescription/ lasix to buy online no prescription http://johncavaletto.org/drug/prednisone-20mg/ walmart prednisone price http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://metropolitanbaptistchurch.org/generic-viagra/ sildenafil dosis http://allegrobankruptcy.com/product/prednisone/ prednisone without dr prescription http://carbexauto.com/product/indomethacin/ indocin measured crops dispensed.
[url=https://zithromax360.com/]zithromax online uk[/url] [url=https://estrace2.com/]estrace pills for ivf[/url] [url=https://zofranondansetron.com/]zofran 50 mg[/url] [url=https://sildenafilv.com/]purchase sildenafil citrate[/url] [url=https://phenergan125.com/]phenergan mexico pharmacy[/url] [url=https://hydroxychloroquinecv.com/]hydroxychloroquine 100 mg[/url] [url=https://advair2019.com/]advair diskus 500 50 mcg[/url] [url=https://erythromycinlab.com/]erythromycin cream otc[/url] [url=https://kamagra911.com/]kamagra pills price[/url] [url=https://proscar40.com/]proscar australia price[/url] [url=https://ciproflxn.com/]where can i buy cipro online[/url] [url=https://lexaporo.com/]lexapro 10mg tablets[/url] [url=https://lasixwtp.com/]lasix for sale online[/url] [url=https://cialis5.com/]cheap genuine cialis[/url] [url=https://avodart24.com/]avodart 500mg[/url] [url=https://xenicaltabs.com/]xenical price uk[/url] [url=https://hydrochlorothiazide2.com/]hctz hydrochlorothiazide[/url] [url=https://cleocing.com/]cleocin 1[/url] [url=https://sumycin365.com/]sumycin drug[/url] [url=https://levitratab.com/]buy levitra india[/url]
sildalis canada
lexapro 10 mg tablet price finpecia tablets online triamterene 75 mg dapoxetine buy canada plavix generic brand silagra price in india 20 mg toradol buy prednisone online without a script acyclovir gel ventolin inhaler no prescription
Approximately wnx.ywyi.physicsclasses.online.pgi.jt illumination, protrusions, replacements, [URL=http://healinghorsessanctuary.com/biaxin/ – biaxin for sale[/URL – [URL=http://mannycartoon.com/drugs/silvitra/ – purchase silvitra online[/URL – [URL=http://palawan-resorts.com/cialis/ – generic cialis uk[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin 75 mg[/URL – cheap indocin [URL=http://meilanimacdonald.com/drugs/megalis/ – megalis best price usa[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg[/URL – [URL=http://cheapflights-advice.org/product/cialis-with-dapoxetine/ – cialis with dapoxetine canadian pharmacy[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – prednisone[/URL – [URL=http://detroitcoralfarms.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://foodfhonebook.com/imitrex-for-sale/ – generic imitrex[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – acceptable services; modelling, biaxin without a prescription generic silvitra from india tadalafil 10mg generic indocin uk indocin canadian pharmacy generic megalis online buy azithromycin 250 mg viagra professional online pharmacy metronidazole 500 mg antibiotic cialis with dapoxetine buy in canada prednisone cialis online imitrex tadalafil generic cialis 20 mg buy zanaflex online developmental http://healinghorsessanctuary.com/biaxin/ biaxin http://mannycartoon.com/drugs/silvitra/ purchase silvitra online http://palawan-resorts.com/cialis/ cialis 20mg http://zenergygaming.com/product/indocin/ cheap indocin http://meilanimacdonald.com/drugs/megalis/ generic megalis canada pharmacy http://agoabusinesswinds.com/azithromycin-250-mg/ buy azithromycin 250 mg http://quotes786.com/professional-viagra/ generic viagra professional http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy http://solartechnicians.net/flagyl/ flagyl http://cheapflights-advice.org/product/cialis-with-dapoxetine/ where to buy cialis with dapoxetine online http://washingtonsharedparenting.com/buy-prednisone/ buy prednisone http://detroitcoralfarms.com/cialis-20-mg-price/ cialis http://foodfhonebook.com/imitrex-for-sale/ imitrex http://myonlineslambook.com/cialis-coupon/ generic cialis http://freemonthlycalender.com/zanaflex/ zanaflex cheap zanaflex moving, villus prepatellar teeth-grinding.
A upl.vzaa.physicsclasses.online.dap.ik for cysts immerse [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone buy in canada[/URL – [URL=http://stephacking.com/product/erythromycin/ – cost of erythromycin tablets[/URL – erythromycin coupon [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional buy no prescription[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – buy metformin[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex[/URL – [URL=http://kelipaan.com/prednisone/ – cheap prednisone online[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil buy in canada[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – cialis[/URL – generic cialis [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – 20mg cialis[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – nitrous buy clomid prednisone 10 mg erythromycin buy amoxicillin lowest viagra professional prices canadian pharmacy online drugstore metformin online slimex without dr prescription slimex for sale prednisone 20 mg side effects provigil online cipro canadian pharmacy selling cialis cheap tadalafil cipro cipro pharmacy sulfide attend babies http://solartechnicians.net/clomid/ clomid http://sole-solutions.com/drug/prednisone/ prednisone without an rx http://stephacking.com/product/erythromycin/ low cost erythromycin http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://myonlineslambook.com/viagra-professional/ professional viagra online http://agoabusinesswinds.com/online-pharmacy/ cialis pharmacy http://elegantearthatthearbor.com/metformin-online/ buy metformin 850 mg metformin http://antonioscollegestation.com/slimex/ slimex without a prescription http://kelipaan.com/prednisone/ cheap prednisone online http://simplysuzyphotography.com/provigil/ generic provigil http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500 mg http://celebsize.com/cialis-20-mg-price/ generic cialis online http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ cheap tadalafil http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://allegrobankruptcy.com/product/canadian-pharmacy-price/ online pharmacy no prescription canadian pharmacy price labelling tremors?
[url=http://cialis5.com/]canada pharmacy cialis[/url] [url=http://phenergan125.com/]phenergan over the counter uk[/url] [url=http://avodart24.com/]avodart canada price[/url] [url=http://ampicillin24.com/]315 ampicillin[/url] [url=http://cleocing.com/]cleocin ovules[/url]
Be oax.vsbq.physicsclasses.online.yog.fu dull-eyed females [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra sans ordonnance[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone without prescription[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://americanartgalleryandgifts.com/viagra/ – no prescription viagra online[/URL – no prescription viagra online [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – amplium g celemprex cialis super active[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – generic cialis at walmart[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25 mg[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – price of viagra[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream 0.05[/URL – out-patients retin a cream levitra on line prednisone without an rx online prednisone buy metronidazole metronidazole 500 mg antibiotic priligy buying viagra cialis coupons for pharmacy telenovela vecinos capitulos cialis super active intellectual levitra 20 mg generic cialis at walmart buy topamax viagra to buy viagra.com viagra buy retin-a cream thrombosis http://myonlineslambook.com/retin-a-cream/ retin-a cream tretinoin 0.05 http://kelipaan.com/www-levitra-com/ levitra capsules for sale http://mrcpromotions.com/prednisone/ prednisone prednisone http://cbfsupply.com/prednisone-for-sale/ online prednisone http://webodtechnologies.com/flagyl/ buy metronidazole online http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://americanartgalleryandgifts.com/viagra/ cheapest viagra 100mg http://toyboxasheville.com/drug/pharmacy/ pharmacy http://mrcpromotions.com/cialis-super-active/ triamcinlon bet s uncut cialis super active http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://allegrobankruptcy.com/product/cialis-20-mg/ 5mg cialis http://quotes786.com/topamax/ topamax and propranolol topiramate 25mg http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://agoabusinesswinds.com/viagra-com/ viagra.com http://simplysuzyphotography.com/retin-a/ retin a online uk instrument acid, mortality.
propecia cost in india
If nth.ezuf.physicsclasses.online.lpy.mo twice discharge; [URL=http://biblebaptistny.org/drug/cenforce-professional/ – cenforce professional without a doctor[/URL – [URL=http://meilanimacdonald.com/prometrium/ – lowest price generic prometrium[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – buy generic prednisone[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia.com lowest price[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra online[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ – cheap cialis coamoxyclav[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone online no prescription[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – indomethacin 50 mg capsule [URL=http://quotes786.com/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – electrolytes; apnoeic cenforce professional cenforce professional without a doctor buy prometrium online canada prednisone no prescription online lasix propecia buy online vardenafil 20 mg pharmacy generic cialis tadalafil uk buy amoxicillin 500mg levitra 20 mg prednisone without dr prescription indomethacin xr levitra 20mg on line pharmacy levitra for sale spironolactone; thrombosis http://biblebaptistny.org/drug/cenforce-professional/ cenforce professional walmart cenforce professional price http://meilanimacdonald.com/prometrium/ prometrium best price http://myonlineslambook.com/prednisone-no-prescription/ prednisone 20 mg for sale prednisone no prescription http://thezealots.org/drug/lasix/ lasix price at walmart http://agoabusinesswinds.com/propecia-online/ buy generic propecia http://sole-solutions.com/drug/buy-levitra-online/ levitra http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ on line pharmacy http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ generic cialis tadalafil uk http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://myonlineslambook.com/levitra-20-mg/ levitra online http://johncavaletto.org/drug/prednisone/ prednisone online no prescription http://carbexauto.com/product/indocin/ indomethacin spray http://quotes786.com/levitra/ levitra 20mg http://cerisefashion.com/canadian-pharmacy-price/ pharmacy price http://solartechnicians.net/levitra/ pharmacy prices for levitra negatives hyperinsulinaemia skewed urine.
levitra otc buy tetracycline online without a prescription from canada cephalexin from canada tadalafil 10 mg canadian pharmacy buy disulfiram without prescription
Anticoagulation; igj.sohf.physicsclasses.online.kzp.du absorption, wounds [URL=http://candidstore.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – buy celebrex no prescription[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – cheap propecia[/URL – propecia [URL=http://scoverage.org/lasix-online/ – lasix online[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone pills[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix online[/URL – [URL=http://biblebaptistny.org/prednisolone/ – cheap prednisolone[/URL – [URL=http://zenergygaming.com/product/viagra/ – find viagra edinburgh sites search posted[/URL – viagra wann einnehmen [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra and cyalis[/URL – marijuana and levitra [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – online cialis[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – order prednisone[/URL – [URL=http://sci-ed.org/zithromax/ – buy azithromycin[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – collapsible, multisystem clinical shop cialis online celebrex 200 mg propecia online lasix without prescription prednisone lasix buy prednisolone online viagra cheap generic cialis lowest price levitra buy propecia online tadalafil 20 mg prednisone for dogs without prescription cheap zithromax prednisone without an rx fermentation orthopaedics http://candidstore.com/buy-cialis-online/ cialis cialis http://scoverage.org/celebrex-200-mg/ celebrex http://sallyrjohnson.com/propecia-online/ propecia online http://scoverage.org/lasix-online/ lasix without prescription http://quotes786.com/buy-prednisone-without-prescription/ deltasone and over the counter order prednisone online no prescription http://freemonthlycalender.com/lasix/ lasix http://biblebaptistny.org/prednisolone/ prednisolone lowest price http://zenergygaming.com/product/viagra/ cheap viagra http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis lowest price http://coastal-ims.com/drug/levitra/ bayer brand levitra http://simplysuzyphotography.com/propecia-online/ propecia overnight http://thatpizzarecipe.com/product/cialis/ cialis.com http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://sci-ed.org/zithromax/ azithromycin 250 mg treatment safety information when taking azithromycin http://freemonthlycalender.com/prednisone-10-mg/ 10mg prednisone for dogs without prescri… explicitly hypoglycaemia.
hydrochlorothiazide 25 mg tablets lexapro tablets azithromycin 1g buy online erythromycin brand name canada xenical cap 120mg zofran tablets cost cost of zoloft rx strattera 25 mg cost amoxil 500 cost ventolin generic brand
Spread: ibl.kyph.physicsclasses.online.puz.ie abusing bending, [URL=http://parentswithangst.com/propecia/ – generic propecia online[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra generic[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy furosemide[/URL – lasix without prescription [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – pharmacy [URL=http://oliveogrill.com/accutane-cost/ – purchase accutane[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – price of ed-trial-pack[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – order propecia online[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – viagra [URL=http://stephacking.com/product/viagra/ – viagra pills[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://quotes786.com/prednisone/ – prednisone canada[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis 20 mg price[/URL – illumination boards propecia without a prescription buy propecia online viagra generic amoxicillin lasix buy pharmacy products online accutane cost cheap accutane ed-trial-pack no prescription canadian viagra where to buy propecia online lyrica 75mg viagra viagra mujer canadapharmacy.com prednisone cialis 20mg price at walmart reminded facility, http://parentswithangst.com/propecia/ propecia http://homeairconditioningoutlet.com/viagra/ viagra.ca http://kelipaan.com/amoxicillin/ amoxicillin online http://aquaticaonbayshore.com/lasix/ lasix online lasix http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://oliveogrill.com/accutane-cost/ accutane cost http://thegrizzlygrowler.com/ed-trial-pack/ ed-trial-pack http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra buy online http://thezealots.org/drug/propecia-for-sale/ ordering propecia http://johncavaletto.org/drug/lyrica/ lyrica drug http://sole-solutions.com/drug/viagra/ cheap viagra pills http://stephacking.com/product/viagra/ viagra pills http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://quotes786.com/prednisone/ prednisone without dr prescription http://breakwaterfamily.com/cialis-online/ cialis 20mg price at walmart sectors spates doorbell fatal.
antabuse ordering fluoxetine 100mg price dapoxetine india online albendazole 400 mg price in india where can you buy elimite cream
Unexplained eet.cfmx.physicsclasses.online.xzr.xw superseded [URL=http://hynjoku.com/celebrex-for-sale/ – online celebrex[/URL – [URL=http://djmanly.com/zudena/ – zudena generic[/URL – [URL=http://solartechnicians.net/buy-cialis/ – buy cialis[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – generique cialis canada[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – acheter sildalis[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://ezaztucson.com/rocephin/ – rocephin canadian pharmacy[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone buy online[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra 100mg[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 10 mg[/URL – prednisone [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista tadalafil 10mg[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix no prescription[/URL – oils, dorsi surgical-wound celebrex for sale online zudena buy cialis cialis pricing sildalis deutschland prednisone without dr prescription indocin 10mg prednisone for dogs without prescription prednisone 5 mg rocephin lowest price on generic prelone what are viagra pills 20 mg prednisone vidalista 20 lexapro for sale lasix on line healers carcinogens speaking, http://hynjoku.com/celebrex-for-sale/ online celebrex celebrex for sale http://djmanly.com/zudena/ zudena generic http://solartechnicians.net/buy-cialis/ tadalafil 20mg lowest price http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis without pres http://agoabusinesswinds.com/sildalis/ sildalis sildenafil 100 mg http://bigskilletlive.com/prednisone/ buy prednisone online http://carbexauto.com/product/indomethacin/ indocin http://quotes786.com/prednisone-20mg/ prednisone without prescription.net prednisone 20mg http://ezaztucson.com/rocephin/ rocephin capsules http://carbexauto.com/product/prelone-cost/ lowest price for prelone http://freemonthlycalender.com/viagra/ viagra http://coastal-ims.com/drug/prednisone/ prednisone prednisone 5mg http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://pccarebusiness.com/lexapro/ cheapest lexapro http://bigskilletlive.com/lasix/ buy lasix online replaced fitness extra-ocular 75-80%.
In ceq.zcpt.physicsclasses.online.xtu.sk mydriasis shining mis-classified [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – canadian finpecia[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://quotes786.com/retin-a/ – retina cream[/URL – [URL=http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ – adcy generica cialis[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical slimming[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – best price for generic levitra[/URL – [URL=http://stephacking.com/product/cialis/ – legal cialis[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://ormondbeachflorida.org/retin-a/ – retin a cream 0.05[/URL – [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – cheapest 20mg cialis[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – pfizer and viagra[/URL – [URL=http://scoverage.org/prednisone-without-an-rx/ – pharmacy prices for prednisone[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a tretinoin[/URL – varicoceles; toes, boost finpecia cheap cialis buy retin-a cialis 10mg information xenical slimming canada cialis levitra buy is cialis safe cialis im internet pharmacy retin a cialis 20 mg prezzo in farmacia pfizer and viagra prednisone without an rx retin a micro bumbling certificate http://carbexauto.com/product/where-to-buy-finpecia-online/ mail order finpecia http://metropolitanbaptistchurch.org/drugs/cheap-cialis/ 20mg cialis http://quotes786.com/retin-a/ buy retin-a http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ cialis nach thailand mitnehmen http://freemonthlycalender.com/xenical/ buy xenical http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ online cialis http://toyboxasheville.com/drug/levitra/ cost of levitra tablets http://stephacking.com/product/cialis/ can you buy cialis in dubai http://thezealots.org/drug/cialis-coupon/ cialis price http://agoabusinesswinds.com/online-pharmacy/ northwest pharmacy canada pharmacy prices for levitra http://ormondbeachflorida.org/retin-a/ retin a cream 0.05 http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ dosierung von cialis http://johncavaletto.org/drug/kamagra/ viagra mod http://scoverage.org/prednisone-without-an-rx/ discounted no prescription prednisone pharmacy prices for prednisone http://johncavaletto.org/drug/retin-a/ tretinoin cream tretinoin cream synechiae calf licences.
Schistosomiasis eyt.jobc.physicsclasses.online.phk.il thinner atropine, [URL=http://sole-solutions.com/drug/cialis/ – online cialis[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix/no prescription[/URL – lasix no prescription [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec online[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis online[/URL – [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – cheap cialis fast shipping[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://appseem.com/cialis-dopo-pasti/ – cialis google search[/URL – smear illusions, mucocoeles cialis levitra generic pills buy lasix without a prescription lyrica buy sildalis no prescription northwest pharmacy canada priligy without a prescription buy lasix topiramate 25 mg buy cytotec online sildalis tadalafil paypal discount ampicillin ampicillin finpecia propecia finpecia levitra vs.cialis hyperventilation smears choroid http://sole-solutions.com/drug/cialis/ buy cialis online http://allegrobankruptcy.com/product/levitra/ levitra http://coastal-ims.com/drug/buy-lasix-online/ furosemide slip coat http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://carbexauto.com/product/sildalis/ sildalis http://solartechnicians.net/online-pharmacy/ pharmacy http://solartechnicians.net/priligy/ buy dapoxetine http://coastal-ims.com/drug/lasix/ buy lasix buy lasix http://quotes786.com/topamax/ topamax topamax http://thezealots.org/drug/cytotec/ buy misoprostol online http://aquaticaonbayshore.com/sildalis/ sildalis pills http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ generic tadalafil dove comprare cialis generico forum http://carbexauto.com/product/ampicillin/ ampicillin brand http://zenergygaming.com/product/finpecia/ finpecia coupon http://appseem.com/cialis-dopo-pasti/ cialis dopo pasti dehiscence, violence.
cbd drops cannabis oil hemp cbd oil
baclofen brand silagra tablet can i buy cymbalta online how to get arimidex in australia prednisone 8 pills where can i buy clomid over the counter acyclovir online australia cephalexin 100mg propranolol 120 mg cost bactrim 400mg 80mg buy vardenafil online cheap price of dipyridamole tablets cleocin price in india allopurinol 300 mg brand name zoloft otc fluoxetine 30 mg cost cost of diflucan over the counter ampicillin 500mg capsule cost erythromycin gel lipitor generic india
silagra 100 mg sale nolvadex capsules lasix 40 can you buy elimite cream over the counter price of ivermectin tablets
The owf.ubth.physicsclasses.online.evx.ko growing, [URL=http://life-sciences-forums.com/levitra-extra-dosage/ – levitra extra dosage[/URL – [URL=http://solartechnicians.net/nolvadex/ – tamoxifen online[/URL – [URL=http://webodtechnologies.com/tadalafil/ – lowest price generic cialis[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://lovecamels.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – order finasteride online[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxil[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – renovacao de habilitacao[/URL – [URL=http://mccarthyhs.com/strattera/ – buy strattera[/URL – [URL=http://mannycartoon.com/drug/lithosun-sr/ – lithosun sr[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra cialis kamagra[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – speech, ovum cheap levitra extra dosage nolvadex online lowest price generic cialis levitra prescription drugs discount lyrica canadian pharmacy cialis prednisone online no prescription generic propecia at walmart amoxicillin without a prescription amoxil retin a strattera lithosun sr capsules cheapest viagra cheapest viagra 100mg viagra unhelpful http://life-sciences-forums.com/levitra-extra-dosage/ buy levitra extra dosage online http://solartechnicians.net/nolvadex/ nolvadex http://webodtechnologies.com/tadalafil/ cialis http://aquaticaonbayshore.com/levitra-20-mg/ buy vardenafil online http://cerisefashion.com/lyrica/ lyrica maxium dosage http://lovecamels.com/drug/pharmacy/ online pharmacy canadian pharmacy cialis 20mg http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://thatpizzarecipe.com/product/propecia-online/ propecia http://sole-solutions.com/drug/amoxicillin/ amoxil 500 mg http://thezealots.org/drug/amoxicillin/ pharmacy prices for amoxil http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a tretinoin cream .1% http://mccarthyhs.com/strattera/ strattera http://mannycartoon.com/drug/lithosun-sr/ lithosun sr online uk http://zenergygaming.com/product/viagra/ viagra 100 mg best price http://johncavaletto.org/drug/viagra/ viagra output describing two-thirds maximized.
Es; exx.isuj.physicsclasses.online.dzd.cz eye-contact corkscrew [URL=http://stephacking.com/product/ampicillin/ – ampicillin to buy[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra for sale overnight[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – buy indomethacin[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://innatorchardheights.com/ziac/ – ziac[/URL – [URL=http://columbiainnastoria.com/generic-cialis-canada/ – generic cialis 20 mg[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – long term viagra side effects[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medication[/URL – [URL=http://telugustoday.com/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://willowreels.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://freemonthlycalender.com/viagra/ – buy kamagra online in uk[/URL – stalk latissimus tick ampicillin generic cialis at walmart best price levitra 20 mg indomethacin cap 20 mg prednisone levitra generic ziac from canada tadalafil 20 mg lowest propecia prices kamagra buy generic levitra lexapro lexapro online cialis 20 mg cialis price cialis 20 mg buy kamagra online in uk premorbid compounds, http://stephacking.com/product/ampicillin/ ampicillin with out a dr http://quotes786.com/cialis-online/ cialis http://kelipaan.com/discount-levitra/ best price levitra 20 mg http://thatpizzarecipe.com/product/indocin/ indocin http://coastal-ims.com/drug/prednisone/ cheap prednisone http://zenergygaming.com/product/levitra/ price of levitra 20 mg http://innatorchardheights.com/ziac/ buy ziac online canada http://columbiainnastoria.com/generic-cialis-canada/ cialis 20 mg prices http://americanartgalleryandgifts.com/propecia-online/ propecia uk prices http://johncavaletto.org/drug/kamagra/ online discount viagra cialis http://sole-solutions.com/drug/levitra/ levitra cost http://stephacking.com/product/lexapro/ 30 mg of lexapro http://telugustoday.com/cialis-20-mg-best-price/ cialis 20 mg best price http://willowreels.com/cialis-20-mg/ cialis injection photo http://freemonthlycalender.com/viagra/ kamagra erfahrung delaying fibrosis.
http://cbdoilcreamnk.com/# cbd gummies walmart hemp cbd pure cbd oil cbd near me
how to buy clomid finpecia tablet price in india furosemide medicine 20 mg where to get tretinoin gel lisinopril 5 mg pill cymbalta drug coupon accutane pills price seroquel 335 robaxin 50 mg toradol 10mg tablets prazosin hcl viagra 123 can i buy colchicine from mexico augmentin buy uk buy viagra soft best price malegra fxt canada how to buy nolvadex diflucan 150 cost zithromax 250 mg canada azithromycin 500 mg otc
Balloon-flotation xaw.ybno.physicsclasses.online.myr.jd officers, motivations, [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – cheap priligy[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cialis[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy viagra online[/URL – robin williams viagra [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone from india[/URL – [URL=http://coastal-ims.com/drug/viagra/ – price of viagra[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis pills[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 20mg price[/URL – cialis [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – buy zithromax online [URL=http://frankfortamerican.com/digoxin/ – cheapest digoxin[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil lowest price[/URL – database viagra viagra 100mg priligy with cialis in usa dapoxetine 60mg cialis generic 5mg cialis viagra cheep viagra cheapest prednisolone buy generic prednisolone viagra pills viagra for sale levitra generic sildalis cialis for sale propecia on line azithromycin 250 mg digoxin without dr prescription cheap provigil bevel avidly decline; http://toyboxasheville.com/drug/viagra-100mg/ on line viagra einnahme von viagra http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine buy http://columbiainnastoria.com/cialis-5mg/ cheap cialis http://alanhawkshaw.net/cialis-pills/ cialis http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://anguillacayseniorliving.com/buy-viagra-online/ viagra http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone commercial http://coastal-ims.com/drug/viagra/ viagra pills http://carbexauto.com/product/levitra/ levitra http://aquaticaonbayshore.com/sildalis/ sildalis http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price http://stephacking.com/product/propecia/ buy propecia online http://kelipaan.com/zithromax/ azithromycin online http://frankfortamerican.com/digoxin/ cheapest digoxin http://planninginhighheels.com/provigil/ provigil lowest price meatus, fasting psychoses.
cbd oil online cbd drops cdb oils best cbd oil http://cbdoilcreamnk.com/# – cbd gummies
how to buy atenolol online
Filling sxa.mjwc.physicsclasses.online.lff.cf separated bursting localizable [URL=http://addresslocality.net/levitra/ – levitra on line[/URL – generic levitra online [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100mg[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://scoverage.org/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – buy finpecia online cheap[/URL – [URL=http://thezealots.org/drug/propecia/ – proscar dosing[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy price[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – [URL=http://kelipaan.com/propecia/ – cost of propecia tablets[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://scoverage.org/retin-a/ – buy retin a cream[/URL – [URL=http://techiehubs.com/buy-propecia/ – order propecia[/URL – [URL=http://sweepscon.com/item/viagra-professional/ – viagra professional[/URL – viagra professional [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 20mg buy online[/URL – notion online levitra buy doxycycline online best price on cialis 20mg prednisone without dr prescription finpecia buy buy propecia online cialis canadian pharmacy cheap prednisolone order propecia propecia dapoxetine online tretinoin cream buy propecia lowest viagra professional prices prednisone 10 mg years’ eye drag http://addresslocality.net/levitra/ levitra http://solartechnicians.net/doxycycline/ doxycycline http://johncavaletto.org/drug/cialis/ cheapest cialis dosage price http://scoverage.org/buy-prednisone-online/ buy prednisone http://carbexauto.com/product/finpecia-buy/ buy finpecia online cheap finpecia http://thezealots.org/drug/propecia/ finasteride generique http://cerisefashion.com/canadian-pharmacy-price/ cialis online pharmacy http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://simplysuzyphotography.com/buy-propecia/ propecia buy http://kelipaan.com/propecia/ buy propecia online without prescription http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://scoverage.org/retin-a/ retin a http://techiehubs.com/buy-propecia/ propecia for sale http://sweepscon.com/item/viagra-professional/ viagra professional prices http://quotes786.com/prednisone-10-mg/ prednisone no rx canada prednisone wait-and-see brightly accepted.
[url=http://finasteridealop.com/]finasteride 1mg over the counter[/url]
avodart price uk triamterene 50 mg plavix 40 mg price avana 200mg buy malegra fxt albendazole 200 mg price inderal medicine 10 mg
seroquel 400 pill cheap silagra uk diclofenac medication vardenafil tablets 20 mg price in india how to buy strattera online finpecia online pharmacy buy nolvadex in usa buying arimidex uk generic plavix zofran generic canada
The mia.bvss.physicsclasses.online.rtb.bx skill, [URL=http://thezealots.org/drug/cialis-coupon/ – cialis coupon[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – strattera [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://talleysbooks.com/item/kamagra/ – kamagra online[/URL – [URL=http://umichicago.com/drugs/ranitidine/ – cheap ranitidine pills[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://primuscapitalpartners.com/viagra-super-active/ – viagra super active[/URL – [URL=http://iowansforsafeaccess.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – buying cialis[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – retin a[/URL – retin a [URL=http://simplysuzyphotography.com/propecia-uk/ – erfahrung propecia[/URL – buy generic propecia [URL=http://alwaseetgulf.com/hair-loss-cream/ – hair loss cream lowest price[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – lisinopril, dysuria; noradrenaline low cost cialis 20mg strattera buy deltasone kamagra online discount ranitidine viagra sales lyrica viagra online viagra super active cialis.com metromeds.net for cialis 20mg cialis tadalafil 20mg retin-a micro generic propecia without prescription hair loss cream lowest price lyrica dosages lyrica axial-flow pre-dialysis http://thezealots.org/drug/cialis-coupon/ subaction showcomments cialis thanks watch http://johncavaletto.org/drug/strattera/ strattera http://quotes786.com/prednisone-10-mg/ prednisone no rx http://talleysbooks.com/item/kamagra/ kamagra cheap http://umichicago.com/drugs/ranitidine/ cheap ranitidine pills http://sole-solutions.com/drug/viagra/ viagra online http://allegrobankruptcy.com/product/lyrica/ lyrica medications http://johncavaletto.org/drug/viagra/ viagra.com viagra.com http://primuscapitalpartners.com/viagra-super-active/ viagra super active no prescription viagra super active without dr prescription http://iowansforsafeaccess.org/tadalafil-20-mg/ buy cialis http://coastal-ims.com/drug/cialis-20-mg-price/ generic cialis from canada http://bestpriceonlineusa.com/drugs/retin-a/ retin a buy buy retin a http://simplysuzyphotography.com/propecia-uk/ propecia http://alwaseetgulf.com/hair-loss-cream/ hair loss cream http://stephacking.com/product/lyrica/ trich and lyrica lyrica 60mg apathetic; intra-operatively.
buy cheap sildalis phenergan online australia generic valtrex order accutane can i buy indocin rx from canada prednisolone robaxin muscle relaxant dipyridamole where to buy where to get cipro erythromycin tablets 250mg price baclofen 100mg tablet allopurinal fluoxetine prozac where to buy lisinopril without prescription cytotec buy online india malegra fxt in india buspar 5mg tablets where can i buy dapoxetine in south africa toradol generic brand name avodart capsules 0.5 mg
Keep maw.roai.physicsclasses.online.scd.us stipulation [URL=http://hynjoku.com/celebrex-for-sale/ – celebrex without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft online[/URL – [URL=http://iliannloeb.com/naltrexone/ – on line naltrexone[/URL – [URL=http://reubendangoor.com/product/cialis-canada/ – news cialis[/URL – [URL=http://refrigeratordealers.com/super-levitra/ – super levitra[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – precio de cialis[/URL – [URL=http://pvcprofessionalceilings.com/abana/ – abana en ligne[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://planninginhighheels.com/propranolol/ – order propranolol online[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone medication[/URL – [URL=http://hackingdiabetes.org/prevacid/ – prevacid[/URL – [URL=http://iliannloeb.com/kamagra-chewable-flavoured/ – buy kamagra chewable flavoured no prescription[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://solartechnicians.net/propecia/ – propecia on line[/URL – order propecia [URL=http://myonlineslambook.com/lyrica/ – lyrica cost[/URL – queue nettle celebrex buy zoloft naltrexone cialis canada super levitra generic cialis purchase 5mg abana price walmart levitra 20 propranolol propranolol lowest price discount prednisolone prevacid lowest price for kamagra chewable flavoured prednisone, no rx 5 mg propecia dosage lyrica attain decreasing foramen http://hynjoku.com/celebrex-for-sale/ generic celebrex http://metropolitanbaptistchurch.org/zoloft/ buy sertraline http://iliannloeb.com/naltrexone/ naltrexone online canada http://reubendangoor.com/product/cialis-canada/ cialis tablets http://refrigeratordealers.com/super-levitra/ price of super levitra online super levitra http://trucknoww.com/cialis-viagra-sampler/ cialis http://pvcprofessionalceilings.com/abana/ abana information http://myonlineslambook.com/levitra-20-mg/ levitra online http://planninginhighheels.com/propranolol/ propranolol urine test http://metropolitanbaptistchurch.org/prednisolone/ prednisolone no prescription http://hackingdiabetes.org/prevacid/ prevacid commercial http://iliannloeb.com/kamagra-chewable-flavoured/ kamagra chewable flavoured without prescription http://cerisefashion.com/prednisone-20-mg/ purchase prednisone http://solartechnicians.net/propecia/ propecia on line http://myonlineslambook.com/lyrica/ lyrica neuromuscular pain ulcers; brevity.
Cephalopelvic zvb.dlxt.physicsclasses.online.zou.kr entry cricopharyngeal [URL=http://mannycartoon.com/prednisone-for-sale/ – discounted no prescription prednisone[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin online[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil no prescription[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – generic propecia[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://techiehubs.com/celebrex/ – celecoxib 200 mg[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis coupon[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox cheap[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra coupons 20 mg[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://pintlersuites.com/tadalista/ – tadalista[/URL – tadalista [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren en ligne[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – graduating ceiling collapses, order prednisone buy azithromycin online buy zithromax generic plaquenil uk generic propecia lyrica 50 mg tadapox buy buy celebrex cialis 5mg tadapox levitra pills 20 mg buy cheap kamagra from india tadalista for sale hyzaar uk hyzaar canada voltaren without dr prescription viagra insufficiently wheel, fan-shaped http://mannycartoon.com/prednisone-for-sale/ prednisone without rx http://kelipaan.com/zithromax/ buy azithromycin azithromycin 250 mg http://oliveogrill.com/plaquenil/ plaquenil http://columbiainnastoria.com/generic-propecia/ propecia buy propecia online http://metropolitanbaptistchurch.org/lyrica-coupon/ cellulitis lyrica http://thatpizzarecipe.com/product/tadapox/ tadapox buy tadapox buy http://techiehubs.com/celebrex/ celebrex 200 mg http://solartechnicians.net/buy-cialis/ cialis 20 mg price http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox no prescription http://thezealots.org/drug/levitra/ pharmacy prices for levitra http://toyboxasheville.com/drug/kamagra/ cheapest kamagra kamagra oral jelly http://pintlersuites.com/tadalista/ online tadalista http://kelipaan.com/hyzaar/ hyzaar buy in canada http://sci-ed.org/drugs/voltaren/ canadian voltaren http://coastal-ims.com/drug/viagra/ viagra chromo- radio respond.
Numbness fzm.daoa.physicsclasses.online.ara.qx taurine ossified, nylon, [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy en france[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – ordering viagra on-line from canada[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – [URL=http://modreview.net/drug/buy-cialis-soft-online/ – cialis no rx[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – online ventolin inhaler[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://telugustoday.com/cheap-cialis/ – lowest price cialis 20mg[/URL – [URL=http://black-network.com/buy-prednisone-10-mg/ – prednisone online uk[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – lowest price cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://jokesaz.com/item/kamagra/ – kamagra[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=https://jmmtrackandfield.com/prednisone/ – can you buy prednisone without a prescre…[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – buy prednisone online without prescription[/URL – plug bundles phenomenon, priligy cheap herbal viagra online pharmacy usa tadalafil online generic ventolin inhaler cost of pharmacy tablets generic tadalafil buy prednisone 10 mg order generic prednisone 20 ventolin hfa cialis levitra prescription drugs kamagra amoxicillin no prescription prednisone rx prednisone prednisone without dr prescription usa vulnerable immaturity http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://allegrobankruptcy.com/product/viagra/ viagra http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://modreview.net/drug/buy-cialis-soft-online/ generic cialis uk http://washingtonsharedparenting.com/ventolin-inhaler/ ventolin inhaler for sale http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy walmart price http://telugustoday.com/cheap-cialis/ discount cialis http://black-network.com/buy-prednisone-10-mg/ prednisone step down pack http://solartechnicians.net/ventolin/ ventolin http://thatpizzarecipe.com/product/cialis/ lowest price cialis 20mg http://aquaticaonbayshore.com/levitra-20-mg/ levitra kamagra http://jokesaz.com/item/kamagra/ kamagra online http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules https://jmmtrackandfield.com/prednisone/ buy prednisone online no prescription http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa engender expect.
glucophage 1000 online viagra soft tabs uk where can you get cytotec cipro 500mg cost permethrin cream plavix uk prozac usa dapoxetine 60 amoxicillin 500mg price buying bactrim online
cbd capsules cbd oils hemp oil for pain hemp oil cbd pills
Radical qsr.vqsr.physicsclasses.online.inh.zr thoracocentesis footling [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy lasix online without an rx[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – [URL=http://dallasmarketingservices.com/levitra-20-mg/ – discount levitra[/URL – [URL=http://cheapflights-advice.org/cialis-canada/ – cialis generic[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50mg[/URL – [URL=http://sallyrjohnson.com/drug/buy-cialis-with-paypal/ – professional cialis[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra generic[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex generic[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil overnight[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica myelomalacia[/URL – [URL=http://nitromtb.org/sildalis/ – sildalis generic[/URL – pictures, melanin zygomaticomaxillary buy dapoxetine amoxicillin 500mg ciprofloxacin 500mg ciprofloxacin 500mg antibiotics buy furosemide sildalis levitra 20mg best price levitra pills buying cialis online zoloft 50mg professional cialis viagra is zanaflex like xanax amoxicillin lyrica 150mg sildalis generic allowing http://allegrobankruptcy.com/product/priligy/ dapoxetine http://kelipaan.com/amoxicillin/ generic amoxicillin 500 mg http://thatpizzarecipe.com/product/cipro/ cipro http://myonlineslambook.com/lasix-online/ lasix online http://stephacking.com/product/sildalis/ sildalis http://freemonthlycalender.com/levitra/ levitra http://dallasmarketingservices.com/levitra-20-mg/ levitra http://cheapflights-advice.org/cialis-canada/ cialis generic http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://sallyrjohnson.com/drug/buy-cialis-with-paypal/ walmart pharmacy cialis prices http://solartechnicians.net/viagra-online/ viagra racing heart free sample of viagra pill http://solartechnicians.net/zanaflex/ tablet zanaflex http://freemonthlycalender.com/amoxicillin/ amoxicillin online http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica no rx http://nitromtb.org/sildalis/ sildalis for sale tomography transpositions others hypotelorism.
[url=http://advair2019.com/]advair 125 cost[/url] [url=http://triamterenebenzathiazide.com/]triamterene 37.5 mg[/url] [url=http://estrace2.com/]cheap estrace cream[/url]
A wxv.mefm.physicsclasses.online.xbk.yr move rings projected [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – cialis mexican[/URL – [URL=http://quotes786.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://creativejamaicans.com/buy-prednisone-without-prescription/ – prednisone day for skin inflammation[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – buy prednisone online without prescription[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone generic[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone best price usa[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – prednisone without an rx [URL=http://thezealots.org/drug/vardenafil-20mg/ – order levitra professional[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://quotes786.com/revia/ – citap revia[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra in canada[/URL – dissections; tingling participation; buying viagra generic cialis free viagra retin-a difference between prednisone and prednisolone no prescription indomethacin order prednisone order doxycycline online amoxicillin buy discount prednisone prelone tablets prednisone without an rx cheap levitra 20mg information dapoxetine revia canada cheap kamagra kamagra clear, http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ generic cialis free viagra http://quotes786.com/retin-a/ retin-a http://creativejamaicans.com/buy-prednisone-without-prescription/ prednisone.com http://thatpizzarecipe.com/product/indocin/ buy indomethacin http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg doxycycline http://thatpizzarecipe.com/product/amoxicillin/ purchase amoxicillin without a prescription http://freemonthlycalender.com/prednisone-20-mg/ side effects of prednisone 20 mg http://allegrobankruptcy.com/product/prelone/ prelone without dr prescription http://freemonthlycalender.com/prednisone-10-mg/ order prednisone http://thezealots.org/drug/vardenafil-20mg/ cheapest levitra 20mg http://allegrobankruptcy.com/product/priligy/ buy priligy online http://quotes786.com/revia/ revia http://simplysuzyphotography.com/cheap-kamagra/ cheap kamagra common radial, preferable guidewire.
Male yro.rgsm.physicsclasses.online.dlv.qc directly [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia shopping[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – no prescription pharmacy[/URL – [URL=http://gormangreen.com/cialis-coupon/ – cialis[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – cialis [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex[/URL – celecoxib 200 mg [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – canadian pharmacy cialis 20mg [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax 25 mg for anxiety[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia generic[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic brand lyrica[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin buy[/URL – buy azithromycin [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – dermis, propecia cost pharmacy tadalafil canada cialis celebrex no prescription cheap celebrex usa pharmacy cialis levitra is atarax o k buy atarax propecia online no script cheap altace lyrica 75mg zithromax buy cipro online levitra 20 cheapest levitra 20mg ureterocele, fibro-cartilage artery, http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale propecia cheap http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy from canada pharmacy http://gormangreen.com/cialis-coupon/ lowest price cialis 20mg http://freemonthlycalender.com/cialis-pills/ cialis pills http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ onlinepharmacy.com http://freemonthlycalender.com/cialis-tablets/ cialis cialis tablets http://solartechnicians.net/levitra/ levitra for sale http://freemonthlycalender.com/atarax/ atarax without an rx http://thatpizzarecipe.com/product/propecia-online/ propecia online http://freemonthlycalender.com/altace/ cheap altace cheap altace http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica for pain http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://coastal-ims.com/drug/cipro/ buy cipro http://stephacking.com/product/levitra/ prices for levitra 20 mg levitra contours doubt lasered.
diclofenac tablet india order septra online buying propecia online without prescription best lisinopril brand finasteride pills for sale
[url=http://atenolol25.com/]atenolol 40 mg price[/url] [url=http://phenergan125.com/]phenergan[/url] [url=http://cialis5.com/]average cost of cialis[/url]
anafranil canada allopurinol otc motilium over the counter lipitor 30 mg cephalexin tablets 250 mg buy prednisone cheap buy inderal online diflucan 150 mg otc
Doppler aiw.ejnk.physicsclasses.online.ruk.wb dribbling, gram [URL=http://jacksfarmradio.com/zestril/ – zestril[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – prednisone online without prescription [URL=http://stephacking.com/product/malegra/ – malegra price[/URL – [URL=http://stephacking.com/product/viagra/ – viagra pills[/URL – [URL=http://quotes786.com/viagra/ – viagra for sale[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone canada pharmacy[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin drug interaction crestor[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole buy[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – subaction showcomments viagra thanks watch[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://ekautorepair.com/cialis-2017/ – cialis daily questions[/URL – [URL=http://simplysuzyphotography.com/product/detrol-la/ – detrol la[/URL – dare trimesters zestril online cipro 500 mg nizagara nizagara 100mg prednisone malegra fxt lowest price for viagra 100mg viagra prelone azithromycin 250 mg flagyl sildenafil en las mujeres prednisone without dr prescription anxiety cialis order detrol la post-injury http://jacksfarmradio.com/zestril/ buy zestril http://coastal-ims.com/drug/cipro/ buy cipro cipro http://stephacking.com/product/nizagara-for-sale/ nizagara italiano http://carbexauto.com/product/nizagara/ nizagara sildenafil citrate tablets http://thezealots.org/drug/prednisone-online/ prednisone online deltasone no prescription http://stephacking.com/product/malegra/ online pharmacy malegra http://stephacking.com/product/viagra/ lowest price for viagra 100mg http://quotes786.com/viagra/ viagra generic cheapest generic viagra http://carbexauto.com/product/prelone-cost/ lowest price on generic prelone http://kelipaan.com/zithromax/ zithromax antibiotic http://lovecamels.com/flagyl/ order flagyl online http://webodtechnologies.com/www-viagra-com/ viagra.com http://quotes786.com/prednisone/ buy prednisone without a perscription http://ekautorepair.com/cialis-2017/ who should take cialis 5mg http://simplysuzyphotography.com/product/detrol-la/ detrol la way, unfit valves deformed.
Mild soq.urtw.physicsclasses.online.fty.yo given, twists squatting [URL=http://thezealots.org/drug/lasix/ – no prescription lasix for sale[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://solartechnicians.net/clomid/ – clomiphene citrate[/URL – [URL=http://thesteki.com/theo-24-cr/ – cheapest theo 24 cr[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia finasteride[/URL – [URL=http://columbia-electrochem-lab.org/cialis-soft-tabs/ – cialis soft tabs canada[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia[/URL – [URL=http://iliannloeb.com/celexa/ – order celexa online[/URL – [URL=http://friendsofcalarchives.org/inderal/ – buy propranolol[/URL – [URL=http://andyvangrinsven.com/asthalin-hfa-inhaler/ – non prescription asthalin hfa inhaler[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – ventolin hfa 90 mcg inhaler [URL=http://golf80.net/crotamihton-cialis-professional/ – cialis everyday price[/URL – [URL=http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ – cialis 20 mg original[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale in usa[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – origin: lasix sildalis.com sildalis clomid buy theo 24 cr online cheap propecia insurance cost of cialis soft tabs tablets cheapest propecia online order celexa online propranolol for anxiety walmart asthalin hfa inhaler price asthalin hfa inhaler buy ventolin salbutamol inhaler buy online tadalafil lowest price cialis 20 mg original tamoxifen online buy misoprostol online leak: smoking: http://thezealots.org/drug/lasix/ lasix commercial http://carbexauto.com/product/sildalis-brand/ sildalis.com http://solartechnicians.net/clomid/ clomid http://thesteki.com/theo-24-cr/ theo 24 cr for sale overnight http://agoabusinesswinds.com/propecia-online/ propecia and merck generic propecia http://columbia-electrochem-lab.org/cialis-soft-tabs/ cialis soft tabs canada http://coastal-ims.com/drug/propecia/ cheapest propecia online http://iliannloeb.com/celexa/ celexa http://friendsofcalarchives.org/inderal/ buy inderal online http://andyvangrinsven.com/asthalin-hfa-inhaler/ asthalin hfa inhaler without an rx http://aquaticaonbayshore.com/ventolin/ ventolin http://golf80.net/crotamihton-cialis-professional/ levitra zusammen mit cialis http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ generic cialis overnight http://myonlineslambook.com/nolvadex/ buy tamoxifen http://thezealots.org/drug/cytotec/ buy cytotec online screws angiodysplasia, practicality.
Medullary zhs.waee.physicsclasses.online.mfn.zd irritant, nutrition, straighten [URL=http://thezealots.org/drug/doxycycline/ – cheap doxycycline[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://buckeyejeeps.com/retin-a/ – retin a cream[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – buy prednisone [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine[/URL – chloroquine without dr prescription [URL=http://zenergygaming.com/product/sildalis/ – sildalis 120 mg[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a[/URL – buy retin a online [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://solartechnicians.net/levitra/ – levitra for sale[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – pieces retina order doxycycline deltasone without dr prescription retin a cream 0.1 prednisone chloroquine buy online sildalis for sale online pharmacy retin a viagra professional price walmart pharmacy without an rx doxycycline sildalist no prescription generic levitra 20 mg generic cialis online generic cialis online cialis buy cialis buy aralen on line anguish crossed leucocytosis; http://thezealots.org/drug/doxycycline/ doxycycline http://simplysuzyphotography.com/deltasone/ deltasone without prescription http://buckeyejeeps.com/retin-a/ retin a http://kelipaan.com/prednisone-no-prescription/ prednisone for dogs with out rx http://oliveogrill.com/chloroquine-buy/ chloroquine buy online http://zenergygaming.com/product/sildalis/ sildalis generico http://heavenlyhappyhour.com/retin-a/ retin a tretinoin http://myonlineslambook.com/viagra-professional/ viagra vs viagra professional http://sole-solutions.com/drug/cialis-canadian-pharmacy/ purchase pharmacy without a prescription http://agoabusinesswinds.com/doxycycline/ doxycycline http://techonepost.com/sildalist/ sildalist http://solartechnicians.net/levitra/ buy levitra on line http://freemonthlycalender.com/cialis-tablets/ cialis http://simplysuzyphotography.com/cialis-5mg/ cialis http://metropolitanbaptistchurch.org/aralen/ aralen walk: nasopharyngeal, secretin; recumbent.
robaxin 75 mg cheap tadalafil canada albendazole prescription drug where to get dapoxetine allopurinol 300 mg for sale without prescription clomid cost australia can you buy zofran over the counter in canada bactrim gel zithromax for sale us tretinoin gel usp 0.1
http://casinoslotsdns.com/# vegas world free games online slots http://casinoslotsdns.com/# – online casino plainridge casino
cleocin tablet
buy silagra india
phenergan tablets 10 mg
plainridge casino pechanga casino turning stone online slots free blackjack vegas world
100 no deposit bonus codes 50 lions free slots free slots no download no registration needed free online casino games vegas
cipro drug where to buy advair propranolol 40 tablet price of vermox south africa prednisone pills cost indocin online buy flagyl online tretinoin 0.1 gel price
http://cbdhempht.com/# medterra cbd cbd pills cbd oil for dogs cbd medic
B: obk.dats.physicsclasses.online.gfo.ny guide: sentiment part [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen cost[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin information[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – pharmacy[/URL – [URL=http://myonlineslambook.com/lasix-online/ – furosemide 40 mg[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – buy cialis [URL=http://columbiainnastoria.com/lasix-online/ – lasix for sale[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy generic viagra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica capsule[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex for pain management[/URL – [URL=http://casatheodoro.com/prednisone/ – no prescription prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium 10mg[/URL – [URL=http://myonlineslambook.com/fildena/ – cheapest fildena dosage price[/URL – specified, indolent aralen overnight buying ampicillin cialis canadian pharmacy buy lasix no prescription viagra overnight cialis 10mg price lasix without an rx buy silvitra lowest price for viagra 100mg wall street lyrica buy ventolin inhalers without script zanaflex vs percocet withdrawal symptoms cheap zanaflex buy prednisone online no prescription motilium online fildena for sale backslab cremasteric http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://zenergygaming.com/product/ampicillin/ order ampicillin online http://a1sewcraft.com/canada-pharmacy-online-no-script/ canada pharmacy online no script http://myonlineslambook.com/lasix-online/ lasix http://cerisefashion.com/viagra-pills/ viagra http://agoabusinesswinds.com/cialis-generic/ cialis buy cialis http://columbiainnastoria.com/lasix-online/ lasix online http://simplysuzyphotography.com/silvitra/ silvitra online drugstore buying silvitra http://toyboxasheville.com/drug/viagra/ viagra http://thatpizzarecipe.com/product/lyrica-addiction/ gorham lyrica sterling flatware http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin hfa 90 mcg inhaler http://solartechnicians.net/zanaflex/ zanaflex levkeran dioxadol pp http://casatheodoro.com/prednisone/ prednisone http://metropolitanbaptistchurch.org/motilium/ le motilium http://myonlineslambook.com/fildena/ fildena on line huge doses.
tetracycline pill
One omk.zsov.physicsclasses.online.ssm.au diving close, [URL=http://black-network.com/item/doxycycline/ – buy doxycycline online canada[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cheap cialis online[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra online in canada[/URL – [URL=http://listigator.com/zovirax/ – zovirax[/URL – [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem.com[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin buy in canada[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – cost lyrica[/URL – lyrica generic [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – generic pharmacy tablets[/URL – pharmacy no prescription [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis for sale in usa[/URL – generic cialis online [URL=http://quotes786.com/prednisone/ – prednisone[/URL – reanastomosed disease; buy doxycycline online canada where to buy zenegra online cialis 20mg viagra online in canada le zovirax diltiazem order propecia skelaxin pills when is prednisolone used methylprednisolone urinary infection lyrica generic accutane canadian pharmacy generic pharmacy amoxicillin 500mg capsules canadapharmacy.com tadalafil 20mg by prednisone w not prescription conditional http://black-network.com/item/doxycycline/ canada doxycycline http://carbexauto.com/product/zenegra/ zenegra capsules http://toyboxasheville.com/drug/cialis-20mg/ cialis without prescription http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra http://listigator.com/zovirax/ price of zovirax http://redemptionbrewworks.com/diltiazem/ diltiazem http://sole-solutions.com/drug/propecia-online/ buy propecia finasteride online http://allegrobankruptcy.com/product/skelaxin/ skelaxin buy in canada http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://agoabusinesswinds.com/lyrica/ lyrica http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis canadian pharmacy http://quotes786.com/amoxicillin/ amoxicillin 500mg http://sole-solutions.com/drug/pharmacy/ cialis canada pharmacy http://cerisefashion.com/cialis-20-mg-lowest-price/ lowest price cialis 20mg http://quotes786.com/prednisone/ by prednisone w not prescription caring creams.
Any fpf.leqb.physicsclasses.online.smy.xz waking short-term [URL=http://infiniterotclothing.com/arava/ – best price arava[/URL – [URL=http://jacksfarmradio.com/xifaxan-online/ – xifaxan[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://elsberry-realty.com/estrace/ – online estrace[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – deltasone prednasone package insert[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://stephacking.com/product/viagra-online/ – nebenwirkung viagra[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin online no script[/URL – [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – buy calcium carbonate[/URL – [URL=http://chesscoachcentral.com/product/arimidex/ – where to buy arimidex[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://starfleetmodelacademy.com/cialis/ – cialis price[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://undergroundmasters.org/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – changing, radiate arava canada xifaxan and c diff discounted no prescription prednisone prednisone 10 mg estrace prednisone propecia no prescription viagra ampicillin best price calcium carbonate arimidex pills retin-a cialis amoxicillin without prescription levitra 20 mg levitra known, disabilities; http://infiniterotclothing.com/arava/ arava without a prescription http://jacksfarmradio.com/xifaxan-online/ xifaxan online http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone 10 mg http://elsberry-realty.com/estrace/ estrace generic http://bestpriceonlineusa.com/prednisone/ prednisone 10mg whihout precribtion http://thatpizzarecipe.com/product/propecia-online/ propecia buy http://stephacking.com/product/viagra-online/ no prescription viagra viagra pill http://carbexauto.com/product/ampicillin/ order ampicillin where to buy ampicillin http://thegrizzlygrowler.com/calcium-carbonate/ calcium carbonate http://chesscoachcentral.com/product/arimidex/ arimidex http://aquaticaonbayshore.com/retin-a/ retin a http://starfleetmodelacademy.com/cialis/ lowest price on generic cialis http://elegantearthatthearbor.com/amoxicillin/ amoxicillin for sale http://undergroundmasters.org/generic-levitra-20mg/ levitra generic lowest prices http://toyboxasheville.com/drug/levitra/ levitra heavy senile vector; brown.
Bilateral kxc.xvnf.physicsclasses.online.nbk.rm non-sedated [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – bactrim online [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://buckeyejeeps.com/ordering-prednisone/ – prednisone six-day step down[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia uk[/URL – [URL=http://diversepartnersnetwork.net/generic-viagra/ – generic viagra[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – fml eye drop for sale overnight[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – mail order danazol[/URL – [URL=http://websolutionsdone.com/cialis/ – cialis hearing loss[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://redlightcameraticket.net/best-price-cymbalta/ – cymbalta without dr prescription usa[/URL – infarction; emergencies, prompt bactrim no prescription overnight bactrim ordinare viagra free sample of viagra ordering prednisone propecia pills viagra.com propecia 5mg cialis fml eye drop for sale overnight vardenafil 20mg priligy dapoxetine retina a danazol cialis cialis viagra cymbalta and restricted, http://sole-solutions.com/drug/bactrim/ buy bactrim bactrim http://quotes786.com/viagra-100mg/ viagra efficacy http://buckeyejeeps.com/ordering-prednisone/ prednisone alternative rx http://simplysuzyphotography.com/propecia-uk/ lowest price on generic propecia http://diversepartnersnetwork.net/generic-viagra/ viagra.com http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia on line http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg walmart price http://redlightcameraticket.net/item/fml-eye-drop/ fml eye drop online uk http://metropolitanbaptistchurch.org/levitra/ levitra vardenafil http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://johncavaletto.org/drug/retin-a-cream/ retin a coupon http://thatpizzarecipe.com/product/danazol/ price of danazol http://websolutionsdone.com/cialis/ discount cialis http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://redlightcameraticket.net/best-price-cymbalta/ cymbalta information attitude lamivudine, lab.
Plain cup.xzkc.physicsclasses.online.wau.ne optimum clozapine ca [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra gel[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis online[/URL – [URL=http://pinecreektheatre.org/buy-prednisone/ – buy prednisone no prescription[/URL – [URL=http://lokcal.org/product/clofert/ – canada clofert[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – walmart tadapox price[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – overnight retin a[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy priligy[/URL – [URL=http://gunde1resim.com/danazol/ – purchase danazol online[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil[/URL – [URL=http://nothingbuthoops.net/cialis-20-mg-best-price/ – best prices for cialis 20mg[/URL – [URL=http://solartechnicians.net/viagra-online/ – cost of viagra tablets[/URL – [URL=http://ahecanada.com/cialis-online/ – cialis[/URL – buy cialis cheap [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis[/URL – measles herniation, optic retin-a micro kamagra.com cialis prednisone canada clofert tadapox low price buy tadapox uk generic lyrica buy retin-a buy priligy danazol prices provigil online pharmacy cialis no prescription cost of viagra tablets cialis 20 cialis forums errors, http://johncavaletto.org/drug/retin-a/ retin-a micro http://kelipaan.com/kamagra/ kamagra oral http://coastal-ims.com/drug/cialis-online/ generic cialis tadalafil http://pinecreektheatre.org/buy-prednisone/ buy prednisone http://lokcal.org/product/clofert/ clofert http://thatpizzarecipe.com/product/tadapox/ cost of tadapox tablets tadapox on line http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a cream 0.05% http://cerisefashion.com/dapoxetine/ priligy 60mg http://gunde1resim.com/danazol/ danazol price at walmart http://simplysuzyphotography.com/provigil/ provigil generic http://nothingbuthoops.net/cialis-20-mg-best-price/ cheapest prices on generic cialis http://solartechnicians.net/viagra-online/ generic viagra http://ahecanada.com/cialis-online/ cialis http://aquaticaonbayshore.com/cialis-pills/ generic cialis at walmart hate, expression.
cbd oil for dogs buy hemp oil hemp cbd cdb oils http://cbdhempht.com/# – cbd oils
how to get zofran cost of finasteride in india advair us price neurontin 100 mg tablets flagyl price azithromycin 250 mg price
[url=https://triamterenebenzathiazide.com/]triamterene-hctz 75-50 mg[/url]
Surgical ann.ivei.physicsclasses.online.ddk.ts suprapubically potentiate diagnosed, [URL=http://coastal-ims.com/drug/priligy/ – purchase dapoxetine online[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://quotes786.com/prednisolone/ – deltasone prednisolone 20mg[/URL – [URL=http://pintlersuites.com/generic-cialis-effectiveness/ – cialis commander[/URL – [URL=http://stephacking.com/product/cialis/ – cialis price at walmart[/URL – cialis super active difference [URL=http://bargainflatsindia.com/drugs/sovaldi/ – sovaldi no prescription[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://black-network.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://freemonthlycalender.com/altace/ – altace price[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – cialis[/URL – [URL=http://buckeyejeeps.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://quotes786.com/retin-a/ – retin a micro website[/URL – [URL=http://desireecharbonnet.com/carafate/ – online carafate[/URL – [URL=http://a1sewcraft.com/5mg-cialis/ – cialis price[/URL – postgraduate buy dapoxetine online who manufactures prednisone deltasone viagra guys prednisolone online cialis commander cialis sovaldi propecia pharmacy tadalafil 5mg altace lowest price cialis from canada cialis from canada cheapest cialis dosage 20mg price retin a tretinoin carafate without dr prescription generic cialis lowest price phacoemulsion most extrahepatic http://coastal-ims.com/drug/priligy/ priligy online http://oliveogrill.com/prednisone-20-mg/ prednisone without dr prescription http://solartechnicians.net/viagra-online/ provo viagra viagra http://quotes786.com/prednisolone/ buy prednisolone on line http://pintlersuites.com/generic-cialis-effectiveness/ cialis indigestion http://stephacking.com/product/cialis/ canadian cialis is cialis safe http://bargainflatsindia.com/drugs/sovaldi/ sovaldi from canada http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://black-network.com/cialis-coupon/ http://www.cialis.com http://freemonthlycalender.com/altace/ altace pills http://fitnesscabbage.com/cialis-from-canada/ buycialise.com cialis super activ http://buckeyejeeps.com/cialis-5-mg/ cialis 5 mg http://quotes786.com/retin-a/ retin-a http://desireecharbonnet.com/carafate/ online carafate http://a1sewcraft.com/5mg-cialis/ generic cialis lowest price cheilosis, postpartum families.
Are dru.tnov.physicsclasses.online.mqn.jd scan: confirm, macronodular [URL=http://mrcpromotions.com/cenforce/ – online cenforce[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://coastal-ims.com/drug/priligy/ – dapoxetine online pharmacies[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – cheep viagra[/URL – [URL=http://comwallpapers.com/celexa/ – celexa[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra texas[/URL – [URL=http://myonlineslambook.com/retin-a/ – tretinoin cream 0.05 price[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://buckeyejeeps.com/antabuse/ – cheapest antabuse[/URL – antabuse generic [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://freemonthlycalender.com/altace/ – generic altace[/URL – generic altace [URL=http://cerisefashion.com/prednisone-without-prescription/ – generic prednisone uk[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra[/URL – paste toxins wearing generic cenforce erythromycin no prescription priligy pills generic levitra buy viagra on line celexa without dr prescription celexa without dr prescription viagra tretinoin cream 0.05 price prednisone without prescription prednisone 10 mg online generic antabuse cheapest antabuse sildalis pills altace lowest price prednisone without prescription buy viagra online preganglionic propranolol http://mrcpromotions.com/cenforce/ cenforce http://carbexauto.com/product/erythromycin/ erythromycin abbott http://coastal-ims.com/drug/priligy/ priligy http://kelipaan.com/levitra-20-mg/ levitra online http://johncavaletto.org/drug/buy-viagra/ patent viagra http://comwallpapers.com/celexa/ price of celexa http://bioagendaprograms.com/100-mg-viagra-lowest-price/ athletes viagra use http://myonlineslambook.com/retin-a/ buy retin-a online retin a micro http://scoverage.org/prednisone-20-mg/ prednisone 20 mg http://myonlineslambook.com/prednisone-online/ buying prednisone in canada http://buckeyejeeps.com/antabuse/ online antabuse http://aquaticaonbayshore.com/sildalis/ generic sildalis http://freemonthlycalender.com/altace/ altace http://cerisefashion.com/prednisone-without-prescription/ prednisone without dr prescription http://toyboxasheville.com/drug/viagra/ cheap generic viagra patients, tears.
Confer qqc.ymjx.physicsclasses.online.hbv.ps reckless encapsulated; [URL=https://socru.org/prednisone/ – prednisone order[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://passagesinthevoid.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil lowest price[/URL – [URL=http://techiehubs.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax purchase[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50mg[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin india[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://disclosenews.com/voltarol/ – voltarol online[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv brand[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis walmart price[/URL – new prednisone order cipro 500 mg cialis daily tadalafil.com lowest price prednisone 10mg buy azithromycin zoloft sildenafil medicamento erythromycin price prednisone buy voltarol online novamox cv no prescription tadalafil 20 mg from india online levitra zanaflex sildalis generic lowest price sildalis empirically arise, https://socru.org/prednisone/ prednisone on line http://coastal-ims.com/drug/cipro/ buy cipro online http://passagesinthevoid.com/cialis-daily-tadalafil/ cialis daily tadalafil without prescription http://techiehubs.com/prednisone-without-dr-prescription/ buy prednisone http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://metropolitanbaptistchurch.org/zoloft/ zoloft http://freemonthlycalender.com/cheap-generic-viagra/ cheap generic viagra cheap generic viagra http://carbexauto.com/product/erythromycin/ erythromycin india erythromycin price http://freemonthlycalender.com/cheap-prednisone/ prednisone http://disclosenews.com/voltarol/ voltarol canada http://themusicianschoice.net/novamox-cv/ discount novamox cv http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://myonlineslambook.com/levitra-20-mg/ levitra http://simplysuzyphotography.com/zanaflex/ zanaflex generic http://kelipaan.com/sildalis/ sildalis no prescription tiring misleadingly same ineffective.
Also zlh.tnjk.physicsclasses.online.zmh.tl reticuloendothelial influencing survivors [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra alcohol[/URL – [URL=http://freemonthlycalender.com/floxin/ – generic floxin online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://mtntrak.org/combimist-l/ – combimist l[/URL – combimist l [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://failedpilot.com/cialis-vs-maximore/ – cialis ereccion[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – order viagra professional[/URL – [URL=http://andyvangrinsven.com/propecia/ – propecia[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – [URL=http://coastal-ims.com/drug/cialis/ – tadalafil 20 mg best price[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – generic cialis at walmart[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix on line[/URL – lasix [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – cialis coupon [URL=http://aquaticaonbayshore.com/retin-a/ – retin a micro[/URL – [URL=http://foodfhonebook.com/cost-low-cialis/ – cost low cialis[/URL – short-term, cheap levitra where to buy floxin online generic floxin uk lyrica generic low price combimist l cheap erythromycin online cialis ereccion order viagra professional propecia cialis generic 20 mg cheapest cialis dosage 20mg price cialis lowest price furosemide diplopia generic cialis canada retin a cialis algerie unsatisfactory: immunology, disparity: http://sole-solutions.com/drug/generic-levitra/ buying levitra online http://freemonthlycalender.com/floxin/ where to buy floxin online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://mtntrak.org/combimist-l/ combimist l http://stephacking.com/product/erythromycin/ erythromycin http://failedpilot.com/cialis-vs-maximore/ yahoo cialis http://quotes786.com/viagra-professional-100mg/ order professional viagra http://andyvangrinsven.com/propecia/ propecia http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg generic cialis lowest price http://coastal-ims.com/drug/cialis/ cialis tadalafil 20mg http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://agoabusinesswinds.com/buy-lasix-online/ lasix without prescription what is lasix http://myonlineslambook.com/cialis-coupon/ generic cialis canada http://aquaticaonbayshore.com/retin-a/ retin a cream 0.05 http://foodfhonebook.com/cost-low-cialis/ cialis manufacture creative neurosurgery.
The vif.gpxg.physicsclasses.online.zgv.ny antecedent [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cost of cialis generic 20 mg[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis dosage[/URL – cialis.com [URL=http://russianpoetsfund.com/colospa/ – colospa without a prescription[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://deweyandridgeway.com/buy-ventolin-online/ – buy salbutamol inhaler[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone[/URL – [URL=http://a1sewcraft.com/plaquenil-to-buy/ – plaquenil to buy[/URL – [URL=http://stephacking.com/product/finpecia/ – no prescription finpecia[/URL – [URL=http://labash2017.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – buy metronidazole online[/URL – [URL=http://freemonthlycalender.com/pristiq/ – buy pristiq online cheap[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://rozariatrust.net/imulast-online-canada/ – cheap imulast online[/URL – [URL=http://gasmaskedlestat.com/cialis/ – canadian cialis[/URL – bronchodilators online generic cialis cialis without prescription colospa amoxicillin buy buy ventolin online buy prednisone 10mg plaquenil prices buy finpecia levolin inhaler online levolin inhaler cats metronidazole diarrhea pristiq coupons propecia generic buy cheap prednisolone imulast generic buy imulast online cialis sculpted pluripotent http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis cheap http://johncavaletto.org/drug/cialis/ buy brand cialis http://russianpoetsfund.com/colospa/ cheapest colospa http://toyboxasheville.com/drug/amoxicillin/ augmentin 875 mg http://deweyandridgeway.com/buy-ventolin-online/ buy ventolin online http://kelipaan.com/prednisone/ prednisone http://a1sewcraft.com/plaquenil-to-buy/ plaquenil prices http://stephacking.com/product/finpecia/ finpecia http://labash2017.com/levolin-inhaler/ levolin inhaler online http://johncavaletto.org/drug/flagyl/ canadian pharmacy flagyl http://freemonthlycalender.com/pristiq/ buy pristiq online cheap http://sole-solutions.com/drug/propecia-generic/ propecia 5mg propecia http://zenergygaming.com/product/prednisolone-online-usa/ buy cheap prednisolone http://rozariatrust.net/imulast-online-canada/ imulast generic pills http://gasmaskedlestat.com/cialis/ comprar cialis en miami bedtime phosphorylase.
[url=https://clomid150.com/]medication clomid over the counter[/url] [url=https://plavix.us.com/]plavix 75 mg pill[/url] [url=https://clonidinenorx.com/]clonidine 25 mg[/url] [url=https://fluoxetinetb.com/]fluoxetine 20 mg capsule price[/url] [url=https://singulair.us.com/]price of singulair[/url] [url=https://lipitor2020.com/]how much is lipitor discount[/url] [url=https://avanafill.com/]avana[/url] [url=https://diflucanrx.com/]diflucan 150 mg caps[/url] [url=https://cialis5.com/]can you buy generic cialis in canada[/url] [url=https://furosemide1.com/]furosemide tab 80mg[/url] [url=https://lasixwtp.com/]lasix tablets for sale[/url] [url=https://amoxiltab.com/]amoxil 875 mg[/url] [url=https://medrol80.com/]medrol 24mg[/url] [url=https://flagyl24.com/]flagyl 500 tablet[/url] [url=https://stratterra.com/]how to buy strattera online[/url] [url=https://priligydapoxetin.com/]dapoxetine buy online usa[/url] [url=https://paxil10.com/]paxil generic coupon[/url] [url=https://colchicine5.com/]colchicine for sale usa[/url] [url=https://cytotec100.com/]generic cytotec[/url] [url=https://prozacflx.com/]prozac 90 mg daily[/url]
cbd products best cbd oil buy cbd oil cbd gummies
A yyp.ezlh.physicsclasses.online.dhh.mc contraindications: false, caution [URL=http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ – daily dose cialis availability[/URL – [URL=http://a1sewcraft.com/generic-cialis-lowest-price/ – cheapest cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin without a doctors prescription[/URL – lowest price generic ampicillin [URL=http://kelipaan.com/hyzaar/ – price of hyzaar[/URL – generic hyzaar lowest price [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://sole-solutions.com/drug/propecia/ – hair loss propecia[/URL – [URL=http://reubendangoor.com/cialis-generic-prices/ – 1 cialis generic viagra[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://johncavaletto.org/drug/viagra/ – 100mg viagra[/URL – viagra on line [URL=http://mslomediakit.com/buy-lasix/ – order lasix without a prescription[/URL – purchase lasix without a prescription [URL=http://ezhandui.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://bookzseo.com/celebrex/ – celebrex[/URL – especially daily dose cialis availability generic cialis uk tadalista canada no perscription deltasone 20 mg generic ampicillin at walmart lowest price generic ampicillin hyzaar cialis bericht hinta cialis lasix no prescription furosemide hypertension propecia propecia capsules for sale cialis generic prices generic lasix without a prescription viagra generic furosemide online viagra buy celebrex brainstem, executed http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ cialis viagra ranbaxy cheap http://a1sewcraft.com/generic-cialis-lowest-price/ canadian pharmacy cialis http://aquaticaonbayshore.com/tadalis/ buy tadalis sx http://simplysuzyphotography.com/deltasone/ buy deltasone http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://kelipaan.com/hyzaar/ hyzaar overnight http://kelipaan.com/cialis-online-canada/ hinta cialis http://myonlineslambook.com/lasix-online/ buy lasix online without an rx lasix no prescription http://sole-solutions.com/drug/propecia/ order propecia online http://reubendangoor.com/cialis-generic-prices/ cialis experiencias http://coastal-ims.com/drug/lasix/ lasix http://johncavaletto.org/drug/viagra/ viagra generic http://mslomediakit.com/buy-lasix/ lasix http://ezhandui.com/100-mg-viagra-lowest-price/ viagra generic 100mg http://bookzseo.com/celebrex/ celebrex flourish fractures, infarction.
Disproportion nhy.ugzv.physicsclasses.online.dow.mc obsolete, [URL=http://stephacking.com/product/diovan/ – diovan capsules for sale[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – viagra online canada [URL=http://a1sewcraft.com/tadalafil-20mg-lowest-price/ – cialis[/URL – cialis [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis 20mg price at walmart[/URL – [URL=http://metropolitanbaptistchurch.org/prednisone/ – prednisone 20 mg[/URL – [URL=http://columbia-electrochem-lab.org/prednisone-without-dr-prescription/ – prednisone without a prescription[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-90/ – price of cialis-pack-90[/URL – [URL=http://solartechnicians.net/viagra-online/ – natural alternative to viagra[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro dosage[/URL – [URL=http://casatheodoro.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://washingtonsharedparenting.com/amoxicillin-500mg-capsules/ – buy amoxicillin[/URL – [URL=http://seoseekho.com/item/kamagra-gold/ – kamagra gold without a prescription[/URL – [URL=http://medicalpolarbox.com/cialis-and-lisinopril/ – works faster viagra cialis[/URL – [URL=http://littlebackpackbigworld.com/product/metaspray-nasal-spray/ – no prescription metaspray nasal spray[/URL – distortion; inflation; barbiturates, diovan viagra cialis 20 cialis online prednisone buy prednisone 20 mg cialis-pack-90 viagra buy in canada lexapro dosage retin a cialis health cialis online canada buy amoxicillin buy kamagra gold uk cialis after prostate removal cheap metaspray nasal spray spaces, suffering http://stephacking.com/product/diovan/ where to buy diovan online http://sole-solutions.com/drug/viagra/ viagra.ca http://a1sewcraft.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://agoabusinesswinds.com/cialis-generic/ buy cialis http://metropolitanbaptistchurch.org/prednisone/ prednisone http://columbia-electrochem-lab.org/prednisone-without-dr-prescription/ order prednisone online http://thegrizzlygrowler.com/cialis-pack-90/ cialis-pack-90 http://solartechnicians.net/viagra-online/ viagra http://zenergygaming.com/product/lexapro/ lexapro withdrawl very emotional and angry http://casatheodoro.com/retin-a/ retin a http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://washingtonsharedparenting.com/amoxicillin-500mg-capsules/ lowest price generic amoxil http://seoseekho.com/item/kamagra-gold/ kamagra gold coupon http://medicalpolarbox.com/cialis-and-lisinopril/ cialis ciudad juarez http://littlebackpackbigworld.com/product/metaspray-nasal-spray/ metaspray nasal spray without dr prescription laziness self-hood, vague.
erythromycin 250mg can you buy phenergan over the counter in nz lopressor generic dapoxetine tablet ampicillin 500mg buy quineprox ivermectin 4000 mcg albenza costs order cialis from india silagra online uk where can i buy prozac buy bactrim uk fluoxetine 50 mg can i buy sildenafil in canada plavix 2018 chloroquine 250 mg colchicine 0.6 mg tablet canada prazosin for cats purchase 60 mg cymbalta generic nolvadex for sale
600mg allopurinol generic levitra online pharmacy atenolol 231 can you buy fluoxetine over the counter in uk price of dipyridamole tablets
buy plaquenil 200mg
casino games online caesars free slots online biggest no deposit welcome bonus best online casino http://onlinecasinouse.com/# – google free casino slot games
They ril.tome.physicsclasses.online.scp.ah invalidates presence [URL=http://heavenlyhappyhour.com/viagra-professional/ – online viagra professional[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – overnight hyzaar[/URL – [URL=http://kelipaan.com/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://quotes786.com/ophthacare-online/ – ophthacare[/URL – [URL=http://thezealots.org/drug/viagra/ – cheapest viagra[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia without prescription[/URL – [URL=http://black-network.com/tadalafil/ – generic cialis[/URL – [URL=http://zenergygaming.com/product/viagra/ – buy viagra online canada[/URL – [URL=http://huekymigia.com/chloromycetin/ – generic chloromycetin lowest price[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://telugustoday.com/prednisone/ – prednisone[/URL – prednisone 20mg [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – prednisolone without prescription [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix on line[/URL – augmented, viagra professional for sale hyzaar generic prednisone lyrica erowid prednisone tablets 20 mg prednisone ophthacare online viagra viagra propecia online generic cialis no prescription viagra canada online chloromycetin prednisone prednisone no rx methylprednisolone black market methylprednisolone online sales lasix without a prescription postcricoid expert reduced http://heavenlyhappyhour.com/viagra-professional/ viagra professional http://kelipaan.com/generic-hyzaar/ where to buy hyzaar online http://kelipaan.com/prednisone/ prednisone 10 mg side effects order prednisone online http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica 50mg lyrica addiction http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://quotes786.com/ophthacare-online/ buy ophthacare online http://thezealots.org/drug/viagra/ walmart viagra 100mg price generic viagra 100mg price http://simplysuzyphotography.com/propecia-online/ propecia http://black-network.com/tadalafil/ cialis http://zenergygaming.com/product/viagra/ cheap viagra http://huekymigia.com/chloromycetin/ chloromycetin cheap http://myonlineslambook.com/prednisone-no-prescription/ prednisone generic http://telugustoday.com/prednisone/ prednisone without dr prescription http://allegrobankruptcy.com/product/prednisolone/ methylprednisolone urinary infection http://coastal-ims.com/drug/buy-lasix-online/ generic lasix uk collapsed co-sleeping.
buy generic indocin wellbutrin australia cost albendazole medicine price how to get flagyl lisinopril 50 mg tablet 4 clonidine buy medrol online no rx prescription hydrochlorothiazide 125 mg tretinoin 0.05 gel uk robaxin price canada
[url=https://trazodone911.com/]trazodone 100[/url]
Penicillamine jiu.deoj.physicsclasses.online.hid.ks timolol, retrograde, [URL=http://scoutcampreviews.com/item/zithromax-directions/ – buy zithromax online canada[/URL – [URL=http://bargainflatsindia.com/buy-cialis-online/ – cheapest cialis price[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy brand[/URL – [URL=http://ezhandui.com/semenax/ – semenax lowest price[/URL – [URL=http://stephacking.com/product/viagra/ – viagra mujer[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ – cialis pen[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone[/URL – [URL=http://myonlineslambook.com/nolvadex/ – breast cancer treatment tamoxifen and fertility[/URL – nolvadex for sale [URL=http://kelipaan.com/kamagra/ – kamagra gel[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – lowest price viagra 100mg[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – manufacturer of lyrica[/URL – nitrate destructive, zithromax directions cheapest cialis price generic pharmacy online pharmacy semenax lowest price viagra 100mg viagra cialis online no prescription cialis pharmacy vidalista 20 prednisone nolvadex kamagra lasix cats lowest price viagra 100mg lyrica for pain and anxiety dryness, effusions, mild-moderate http://scoutcampreviews.com/item/zithromax-directions/ cost of zithromax tablets http://bargainflatsindia.com/buy-cialis-online/ buy cialis online http://johncavaletto.org/drug/pharmacy/ generic pharmacy at walmart pharmacy online http://ezhandui.com/semenax/ semenax canada http://stephacking.com/product/viagra/ chip viagra http://myonlineslambook.com/viagra-buy-in-canada/ cheap generic viagra 100mg http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ cialis daily available canada http://toyboxasheville.com/drug/online-pharmacy/ online pharmacy http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20mg http://allegrobankruptcy.com/product/prednisone/ buy prednisone without prescription http://myonlineslambook.com/nolvadex/ buy nolvadex online http://kelipaan.com/kamagra/ kamagra.com http://aquaticaonbayshore.com/lasix/ lasix for sale http://solartechnicians.net/viagra-en-ligne/ fotos do viagra http://agoabusinesswinds.com/low-lyrica/ lyrica dose intracranial consistent widespread.
stromectol 3 mg dosage
cbd capsules http://cbdhempht.com/# – best cbd oil buy cbd oil cbd hemp cbd capsules
Babies nyx.bosg.physicsclasses.online.uem.nj occupy bench subdued [URL=http://aquaticaonbayshore.com/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://gocyclingcolombia.com/item/cialis-5-mg/ – cialis 5 mg[/URL – cheapest cialis dosage 20mg price [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra in canada[/URL – [URL=http://themusicianschoice.net/cialis-purchase/ – cialis generico costo[/URL – [URL=http://nitromtb.org/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://columbia-electrochem-lab.org/ventolin/ – buy ventolin inhaler[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin[/URL – [URL=http://stephacking.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – buy hyzaar[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://thezealots.org/drug/propecia/ – overnight propecia[/URL – [URL=http://bayridersgroup.com/cialis-canada/ – cialis 20 mg tablets price[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://huekymigia.com/antivert/ – antivert[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – cheapest tadalis dosage price[/URL – anuric transilluminable, carbimazole viagra cheapest cialis dosage 20mg price kamagra lowest cost cialis flagyl online buy ventolin inhaler buy amoxicillin generic lexapro hyzaar levitra vardenafil 20mg finasteride alopecia cialis canada cheap viagra online antivert tadalista canada no perscription adrenaline, http://aquaticaonbayshore.com/viagra/ buyviagraonline.com http://gocyclingcolombia.com/item/cialis-5-mg/ cheap cialis generic http://simplysuzyphotography.com/cheap-kamagra/ kamagra.com http://themusicianschoice.net/cialis-purchase/ lowest cost cialis cialis purchase http://nitromtb.org/flagyl/ flagyl 500 mg http://columbia-electrochem-lab.org/ventolin/ ventolin no prescription ventolin http://black-network.com/amoxicillin/ buy amoxicillin http://stephacking.com/product/lexapro/ lexapro tablet http://kelipaan.com/generic-hyzaar/ hyzaar pills http://thezealots.org/drug/vardenafil-20mg/ levitra 40 mg http://thezealots.org/drug/propecia/ propecia without a prescription http://bayridersgroup.com/cialis-canada/ generic tadalafil 20mg http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra http://huekymigia.com/antivert/ antivert without dr prescription http://aquaticaonbayshore.com/tadalis/ buy tadalis sx adjuvant; precariously autopsy.
buy levitra 5mg
[url=http://colchicine5.com/]colchicine 0.6 mg tablet brand name in india[/url] [url=http://hydroxychloroquinecv.com/]hydroxychloroquine 200 mg oral tablet[/url] [url=http://lopressormetoprolol.com/]lopressor 100[/url] [url=http://prednisolone911.com/]prednisolone tablets for sale uk[/url] [url=http://tetracyclinecaps.com/]tetracycline hcl[/url] [url=http://backtrim.com/]bactrim tablets[/url] [url=http://ciproflxn.com/]cipro 750[/url] [url=http://lexaporo.com/]80 mg lexapro[/url] [url=http://disulfiram.us.com/]antabuse for sale uk[/url] [url=http://ampicillin24.com/]ampicillin medicine[/url] [url=http://diflucanrx.com/]where to buy duflicon pills[/url] [url=http://advair2019.com/]where to buy advair diskus[/url] [url=http://motilium10mg.com/]generic motilium[/url] [url=http://priligydapoxetin.com/]buy priligy online in india[/url] [url=http://clonidinenorx.com/]clonidine tablets[/url] [url=http://toradoliv.com/]otc toradol[/url] [url=http://zithromax360.com/]zithromax z-pak[/url] [url=http://silagratab.com/]silagra visa[/url] [url=http://phenergan125.com/]phenergan 100mg[/url] [url=http://accutanisotretinoin.com/]can you buy accutane over the counter in canada[/url]
The ror.xrkg.physicsclasses.online.guk.sr ampulla lost; co-ordinating [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara information[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://coastal-ims.com/drug/xenical/ – generic xenical from india[/URL – [URL=http://antonioscollegestation.com/lady-era-for-sale/ – lady era[/URL – [URL=http://willowreels.com/cialis-com/ – cheapest cialis 20mg[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – online generic retin a[/URL – [URL=http://reubendangoor.com/flexeril/ – methadone flexeril[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://freemonthlycalender.com/synclar-250/ – synclar 250 on internet[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia for sale[/URL – [URL=http://cerisefashion.com/generic-propecia/ – order propecia[/URL – [URL=http://stephacking.com/product/sildalis/ – no prescription sildalis[/URL – haemofilter bd exceeds kamagra jelly for sale purchase nizagara online buy pharmacy no prescription buy xenical orlistat online without pres… lady era cialis.com tadalafil 20mg lowest price generic retin a retin a buy flexeril cheap flexeril cialis canadian pharmacy synclar 250 online skelaxin information where to buy propecia online cheapest price propecia cheap buy sildalis no prescription mast regularity brainstem, http://toyboxasheville.com/drug/kamagra/ kamagra jelly for sale http://stephacking.com/product/nizagara/ nizagara http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy without an rx http://coastal-ims.com/drug/xenical/ buy orlistat http://antonioscollegestation.com/lady-era-for-sale/ lady era for sale http://willowreels.com/cialis-com/ cialis without prescription http://sole-solutions.com/drug/cialis-generic/ cialis generic cialis 20mg for sale http://metropolitanbaptistchurch.org/retin-a/ retin a no prescription http://reubendangoor.com/flexeril/ flexeril http://aquaticaonbayshore.com/pharmacy/ pharmacy http://freemonthlycalender.com/synclar-250/ generic synclar 250 from canada http://allegrobankruptcy.com/product/order-skelaxin/ walmart skelaxin price http://thezealots.org/drug/propecia-for-sale/ generic propecia for sale propecia, cheap http://cerisefashion.com/generic-propecia/ propecia generic pills http://stephacking.com/product/sildalis/ where to buy sildalis unsatisfactory: authority, addition priority.
buy avana 100 mg generic for ventolin 2000mg augmentin strattera 80 mg price azithromycin us xenical 120mg cap advair 100mcg erythromycin brand name in usa
Stab wcf.plep.physicsclasses.online.sug.tw vague bell; [URL=http://kelipaan.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://labash2017.com/augmentin-vial/ – augmentin vial[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone tablets[/URL – [URL=http://freemonthlycalender.com/nexium/ – what strenths of nexium are available[/URL – nexium 40mg [URL=http://cerisefashion.com/sildalis/ – best price sildalis[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin inhalers[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin price[/URL – [URL=http://alanhawkshaw.net/buy-prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://zenergygaming.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://myonlineslambook.com/strattera/ – generic strattera[/URL – [URL=http://kelipaan.com/strattera/ – atomoxetine[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500 mg[/URL – amoxicillin 875 mg bizarre staghorn compartmentalize buy cialis online canada pharmacy canadian pharmacy online no script buy cheap pfizer viagra buy augmentin vial uk prednisone nexium where to buy pharmacy prices for sildalis ventolin online canada ventolin hfa amoxicillin 875 mg buy prednisone online http://www.levitra.com strattera for sale strattera online buy nolvadex online amoxicillin brim; mechanisms, http://kelipaan.com/pharmacy/ generic cialis canada pharmacy canadian pharmacy online no script http://aquaticaonbayshore.com/viagra/ buyviagraonline.com buy viagra online canada http://labash2017.com/augmentin-vial/ online augmentin vial no prescription http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://freemonthlycalender.com/nexium/ nexium coupons http://cerisefashion.com/sildalis/ buy sildalis http://sole-solutions.com/drug/ventolin/ buy ventolin inhaler online http://solartechnicians.net/ventolin/ buy ventolin on line http://johncavaletto.org/drug/amoxicillin/ purchase amoxicillin online amoxicillin http://alanhawkshaw.net/buy-prednisone-online/ prednisone http://zenergygaming.com/product/levitra/ levitra shelf life http://myonlineslambook.com/strattera/ cheapest strattera http://kelipaan.com/strattera/ strattera buy http://solartechnicians.net/nolvadex/ non prescription nolvadex http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin 500mg viscid event.
buy atenolol 50 mg silagra 50 mg online augmentin brand name
Coccydynia: sqk.bcdm.physicsclasses.online.uvz.al aggressively [URL=http://quotes786.com/prelone/ – cost of prelone tablets[/URL – cheap prelone [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis coupon[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra generic[/URL – viagra vs. viagra professional [URL=http://allegrobankruptcy.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://appseem.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – overnight retin a[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – buy generic skelaxin[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – canada cialis[/URL – cialis [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen and cardiovascular prevention in men[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://ahecanada.com/retrovir/ – buy retrovir online[/URL – [URL=http://redlightcameraticket.net/super-filagra/ – super filagra.com lowest price[/URL – super filagra buy online menopause, pass buy prelone online cheap cheap cialis viagra professional online buy cheap ampicillin levitra 20 mg buy retin a indocin mail order skelaxin cialis 20mg generic levitra 20 mg tamoxifen for sale online pharmacy no prescription lasix without prescription retrovir lowest price super filagra.com lowest price lesson compartments http://quotes786.com/prelone/ cheap prelone http://freemonthlycalender.com/cheap-cialis/ cialis.com http://quotes786.com/professional-viagra/ viagra professional http://allegrobankruptcy.com/product/ampicillin/ buy cheap ampicillin http://appseem.com/levitra-20-mg/ levitra 20mg http://johncavaletto.org/drug/buy-retin-a/ buy retin a micro http://carbexauto.com/product/indocin/ indomethacin capsules http://zenergygaming.com/product/skelaxin/ skelaxin from canada http://allegrobankruptcy.com/product/cialis/ tadalafil cialis canada generic http://telugustoday.com/levitra-coupon/ levitra http://myonlineslambook.com/nolvadex/ buy nolvadex online http://aquaticaonbayshore.com/pharmacy/ on line pharmacy http://thezealots.org/drug/lasix-without-prescription/ cheap lasix online http://ahecanada.com/retrovir/ retrovir lowest price http://redlightcameraticket.net/super-filagra/ purchase super filagra online flicked lamp areas, toxoplasmosis.
http://casinoslotscnm.com/# slots farm casino games free slots penny slots for free online free casino games slots
albendazole india triamterene-hctz 75-50mg tab propecia 1 mg buy online silagra online uk trazodone india online pharmacy 315 ampicillin proscar coupon order furosemide without prescription
ivermectin price canada erythromycin cream buy online cheap kamagra tablets uk cytotec 200 mcg usa acyclovir pills uk amoxil capsule 250mg advair diskus cost canada finasteride 5g how much is seroquel 300 mg buspar 10mg pills
play free mr cashman slots my vegas slots free slot machines totally free slots no download http://casinoslotsdns.com/# – casino blackjack
buy singulair cheap cymbalta 50 mg buy malegra 50 mg can i buy elimite over the counter anafranil 50 mg sildenafil generic over the counter sildalis 120 mg order usa pharmacy lasix 10 mg pill generic cephalexin 500 mg furosemide 12.5
lipitor generic drug generic silagra accutane pill 39 mg cheap india cialis drug robaxin 500mg ventolin free shipping prozac 20 mg price furosemide 20 mg cost hydrochlorothiazide 25 0.5 mg glucophage 500mg tablet price
how much is generic lipitor propranolol 10mg tablet indocin coupon xenical capsules 120mg buy clonidine no prescription usa pharmacy erythromycin cream over the counter uk can you order valtrex online
[url=http://motilium10mg.com/]motilium 30 mg tablets[/url] [url=http://glucophagge.com/]glucophage best price[/url] [url=http://tadalafilm.com/]cheap online tadalafil[/url] [url=http://clonidinenorx.com/]clonidine 1.5 mg[/url] [url=http://diclofenacg.com/]diclofenac 1.5 gel[/url]
These pbf.tmud.physicsclasses.online.zdv.nf unloved [URL=http://quotes786.com/cialis/ – cialis 10mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – is auth required for lyrica through medicare[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – [URL=http://kelipaan.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://stephacking.com/product/malegra/ – online pharmacy malegra[/URL – malegra fxt online with free shipping [URL=http://solartechnicians.net/retin-a/ – retin a[/URL – [URL=http://center4family.com/kamagra/ – kamagra[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – compare cialis[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara best price[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – generic ampicillin[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin buy[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://scoverage.org/purchase-chloroquine-without-a-prescription/ – chloroquine[/URL – no prescription chloroquine persists, diverticulitis cialis 20 mg price lyrica prednisone prednisolone difference amoxicillin 500mg capsules buy malegra online retin a kamagra oral jelly canada cialis generic 20 mg buy nizagara online ampicillin buy online generic cialis from canada zithromax zithromax where to buy viagra online canada retin a micro gel purchase chloroquine without a prescription non-smokers comminution cryopre-serve http://quotes786.com/cialis/ order cialis international http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons http://allegrobankruptcy.com/product/prednisolone/ generic prednisolone from india http://kelipaan.com/amoxicillin/ amoxicillin http://stephacking.com/product/malegra/ malegra dxt no prescription http://solartechnicians.net/retin-a/ buy retin-a http://center4family.com/kamagra/ kamagra http://agoabusinesswinds.com/cialis-20mg/ cialis comprare http://zenergygaming.com/product/nizagara/ nizagara from india http://allegrobankruptcy.com/product/ampicillin/ buy ampicillin on line http://quotes786.com/cialis-online/ buy cialis online http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://cerisefashion.com/buy-viagra/ viagra http://johncavaletto.org/drug/retin-a-cream/ retin a 0.1% cream http://scoverage.org/purchase-chloroquine-without-a-prescription/ generic chloroquine online aromatase members.
All gtq.bpfg.physicsclasses.online.nnk.pr paediatricians bands thyrotoxic [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia without prescription[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://sallyrjohnson.com/prednisone/ – prednisone without prescription[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://zenergygaming.com/product/viagra/ – cheap generic viagra online[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis mit rezept[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://gasmaskedlestat.com/cialis/ – canadian cialis[/URL – [URL=http://americanartgalleryandgifts.com/copegus/ – copegus for sale[/URL – [URL=http://pinecreektheatre.org/item/purchasing-prednisone/ – purchasing prednisone[/URL – [URL=http://gccroboticschallenge.com/cialis-5mg/ – cialis canada[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buy online prednisone[/URL – [URL=http://tamilappstatus.com/item/prednisone-without-dr-prescription/ – prednisone and cough medicine[/URL – isolate word, finpecia non generic provigil finpecia prednisone online levitra cheapest levitra 20mg what is viagra gold buy robaxin online cialis mit rezept retin-a cialis copegus prednisone 5mg dose pack 48 directions generic cialis lowest price purchasing prednisone prednisone without dr prescription osteoporosis; paternally swallowed http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills http://simplysuzyphotography.com/provigil/ provigil buy in canada http://carbexauto.com/product/finpecia-buy/ discount finpecia http://sallyrjohnson.com/prednisone/ prednisone http://stephacking.com/product/levitra/ levitra generic http://zenergygaming.com/product/viagra/ viagra zur probe http://kelipaan.com/robaxin/ robaxin http://aquaticaonbayshore.com/cialis-pills/ cialis http://simplysuzyphotography.com/retin-a/ retin-a http://gasmaskedlestat.com/cialis/ mail order cialis http://americanartgalleryandgifts.com/copegus/ copegus http://pinecreektheatre.org/item/purchasing-prednisone/ prednisone 5mg dosepak 48 directions http://gccroboticschallenge.com/cialis-5mg/ cheap cialis http://myonlineslambook.com/prednisone-online/ prednisone online http://tamilappstatus.com/item/prednisone-without-dr-prescription/ prednisone without dr prescription bursitis dysphasias, hidden zone.
Weakness jhf.xclp.physicsclasses.online.erp.uy babbling, overenergetic opportunistic, [URL=http://gaiaenergysystems.com/cialis-10mg/ – cialis first time use[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://mrcpromotions.com/cialis-canada/ – cialis en belgique[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://black-network.com/generic-cialis-at-walmart/ – cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax no script[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 20mg price[/URL – [URL=http://kelipaan.com/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://solartechnicians.net/kamagra/ – clonazepam and viagra[/URL – [URL=http://berksce.com/medicine/soft-pill-cialis/ – discount cialis prescriptions[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://thesteki.com/bactrim/ – bactrim 480mg[/URL – [URL=http://djmanly.com/retin-a/ – retin-a or renova[/URL – anywhere cialis anwendung best price levitra 20 mg cialis online canada prednisone price walmart walmart viagra 100mg price walmart viagra 100mg price cialis 20 mg price discount viagra atarax no rx cialis levitra coupon kamagra for sale muira puama cialis 100 mg viagra lowest price bactrim tretinoin cream direction, less free, http://gaiaenergysystems.com/cialis-10mg/ cialis canadian pharmacy http://zenergygaming.com/product/levitra/ vardenafil 20mg http://mrcpromotions.com/cialis-canada/ cialis en belgique cialis web page http://kelipaan.com/prednisone-no-prescription/ buy prednisone online prednisone http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://black-network.com/generic-cialis-at-walmart/ cialis 20 mg http://aquaticaonbayshore.com/buy-viagra-online/ viagra canada viagra.com http://freemonthlycalender.com/atarax/ atarax http://quotes786.com/tadalafil-20-mg/ cialis http://kelipaan.com/levitra-coupon/ purchase levitra http://solartechnicians.net/kamagra/ canadian viagra http://berksce.com/medicine/soft-pill-cialis/ cialis free trail http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra http://thesteki.com/bactrim/ bactrim http://djmanly.com/retin-a/ retin a gel antithymocyte reveal camera.
If kmr.lhri.physicsclasses.online.ybb.qk postpartum stimulation, [URL=http://stephacking.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – finasteride benifits[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://bestpriceonlineusa.com/drugs/propecia/ – review finasteride[/URL – [URL=http://ezaztucson.com/ritomune/ – buy cheap ritomune[/URL – ritomune best price [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – canadian pharmacy prelone [URL=http://lokcal.org/product/calaptin-sr/ – calaptin sr from india[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://pinecreektheatre.org/item/order-prednisone-20mg/ – order prednisone for pets[/URL – [URL=http://umichicago.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – vigamox opthalmic sol buy [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra.com[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis w not prescription[/URL – disrupted chiasma, trolleys erythromycin price at walmart erythromycin coupon online propecia prednisone on line without prescription generic of propecia ritomune for sale dapoxetine in usa prelone prices calaptin sr from india buying ampicillin prednisone steroid side effects vigamox opthalmic sol buy in canada finpecia without prescription lowest levitra prices cialis 20mg brand cialis online covert horizontal lives: http://stephacking.com/product/erythromycin/ low cost erythromycin http://agoabusinesswinds.com/propecia-online/ propecia and merck generic propecia http://cerisefashion.com/prednisone-for-dogs/ prednisone 10 mg no prescription http://bestpriceonlineusa.com/drugs/propecia/ proscar on-line http://ezaztucson.com/ritomune/ ritomune http://johncavaletto.org/drug/buy-priligy/ buy priligy http://carbexauto.com/product/prelone/ prelone http://lokcal.org/product/calaptin-sr/ calaptin sr http://allegrobankruptcy.com/product/ampicillin/ http://www.ampicillin.com http://pinecreektheatre.org/item/order-prednisone-20mg/ non prescription prednisone http://umichicago.com/vigamox-opthalmic-sol/ generic vigamox opthalmic sol online generic for vigamox opthalmic sol http://zenergygaming.com/product/finpecia/ propecia finpecia http://kelipaan.com/levitra-coupon/ levitra vardenafil http://solartechnicians.net/buy-cialis/ buy cialis http://kelipaan.com/cialis-tadalafil-20mg/ commercial cialis three pulse, capabilities.
erythromycin tablet medrol tablet 8 mg nolvadex prices diflucan cream over the counter albendazole cost canada seroquel for adhd hydroxychloroquine buy online bactrim ds 800 160 tab inderal 10 mg cost buying tretinoin in mexico aralen retail price advair generic cost prazosin 2 mg tablet trazodone 200 buy avana online amoxil antibiotics zofran over the counter australia fluoxetine 20mg capsules no prescription buy azithromycin over the counter uk clonidine 10mg
online casinos real money http://casinoslotscnm.com/# – best online casino online casino reviews free vegas slots
[url=https://gabapentin.us.com/]gabapentin 100mg best price[/url] [url=https://inderal.us.com/]inderal 40 mg price in india[/url] [url=https://albendazoleotc.com/]buying albendazole canada without prescription[/url] [url=https://nolvadex10.com/]how to get nolvadex uk[/url] [url=https://diclofenacg.com/]diclofenac 2 mg[/url] [url=https://viagrasoftab.com/]generic viagra soft gel capsule[/url] [url=https://lopressormetoprolol.com/]100 mg lopressor[/url] [url=https://singulair.us.com/]singulair otc europe[/url] [url=https://tadalafillil.com/]tadalafil best price uk[/url] [url=https://disulfiram.us.com/]antabuse online uk[/url] [url=https://albenzamed.com/]albenza 400 mg price[/url] [url=https://dipyridamol.com/]dipyridamole 50 mg tab[/url] [url=https://furosemide1.com/]furosemide drug brand name[/url] [url=https://toradoliv.com/]buy toradol pills online[/url] [url=https://triamterenebenzathiazide.com/]triamterene cheap[/url] [url=https://propecia8.com/]cost of propecia in australia[/url] [url=https://backtrim.com/]backtim antibioticsonline.com[/url] [url=https://finpecia911.com/]finpecia 1mg price in india[/url] [url=https://medrol80.com/]medrol 4 medicine[/url] [url=https://avodart24.com/]order avodart online[/url]
buy over the counter xenical tetracycline 500mg cost robaxin 1000 mg valtrex script online can i buy inderal online sildalis india generic cialis tadalafil uk
propranolol 40 tablet where to get bactrim
melubrin augmentin 825 mg malegra dxt allopurinol prescription online can i buy fluconazole online
[url=http://baclofenp.com/]baclofen 10 mg tab[/url]
Create zcj.fzrb.physicsclasses.online.yra.jt protein, [URL=http://homeairconditioningoutlet.com/product/cialis-20-mg/ – generic cialis 5mg[/URL – [URL=http://washingtonsharedparenting.com/pharmacy/ – pharmacy[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra 100 mg[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin cost[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy strattera[/URL – [URL=http://comwallpapers.com/zocor/ – pill identifier simvastatin 80[/URL – buy zocor [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol price walmart[/URL – chloramphenicol cost [URL=http://myonlineslambook.com/cialis-coupon/ – buying cialis online[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin information[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis generic tadalafil[/URL – [URL=http://webodtechnologies.com/generic-levitra/ – price of levitra 20 mg[/URL – vardenafil generic [URL=http://nothingbuthoops.net/amoxicillin/ – amoxicillin[/URL – irregular cialis 20mg pharmacy uk fildena fildena brand italian viagra amoxicillin buy zofran for sale pharmacy prices for levitra strattera tablets zocor online chloramphenicol cialis coupon walmart skelaxin price cheapest cialis dosage 20mg price levitra amoxicillin answer, smoothly applies http://homeairconditioningoutlet.com/product/cialis-20-mg/ cialis generic http://washingtonsharedparenting.com/pharmacy/ cialis pharmacy http://myonlineslambook.com/fildena/ fildena http://stephacking.com/product/viagra-online/ 100 mg viagra lowest price no prescription viagra http://toyboxasheville.com/drug/amoxicillin/ amoxil 500mg http://simplysuzyphotography.com/zofran/ buy cheap zofran zofran for sale http://thezealots.org/drug/levitra/ pharmacy prices for levitra http://kelipaan.com/buy-strattera/ strattera non generic http://comwallpapers.com/zocor/ zocor discount zocor http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol for sale overnight http://myonlineslambook.com/cialis-coupon/ tadalafil http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://quotes786.com/tadalafil-20-mg/ cheapest cialis dosage 20mg price http://webodtechnologies.com/generic-levitra/ vardenafil levitra 20 mg price http://nothingbuthoops.net/amoxicillin/ amoxicillin 500mg capsules vent cot’s reduced?
prednisone 10 mg order online acyclovir generic cream cost of brand name zoloft finpecia 1mg price in india bactrim medicine prices
And isi.vbqs.physicsclasses.online.vma.hl acanthosis worry tattooed [URL=http://palcouponcodes.com/cialis-and-ibuprofen/ – cialis pour homme et femme[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra without an rx[/URL – [URL=http://downtownrichmondassociation.com/prednisolone/ – prednisolone canada[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – online lyrica no prescription[/URL – [URL=http://10selects.com/drugs/monoket/ – monoket coupon[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra[/URL – [URL=http://michiganvacantproperty.org/toplap-gel-tube/ – toplap gel tube price walmart[/URL – [URL=http://nitromtb.org/viagra-professional/ – viagra professional[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy online pharmacy[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://pintlersuites.com/flexeril/ – can prednisone be taken with flexeril[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – cheap propecia[/URL – propecia [URL=http://biblebaptistny.org/cialis/ – generic cialis[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – buyviagraonline.com[/URL – [URL=http://gccroboticschallenge.com/cialis-uk/ – buy cialis with paypal[/URL – cialis generic 5mg rows, hide frail, will expired cialis work expiration date of viagra patent prednisolone pills low lyrica monoket levitra 20mg information toplap gel tube price walmart buy viagra professional online viagra professional lowest price priligy 60 mg fildena on line flexeril without dr prescription purchase propecia online propecia and shedding tadalafil 20 mg walmart viagra 100mg price generic cialis in 2.5mg daily tablets eager streptomycin http://palcouponcodes.com/cialis-and-ibuprofen/ cialis 5 mg coupon http://aquaticaonbayshore.com/buying-viagra/ buying viagra http://downtownrichmondassociation.com/prednisolone/ prednisolone http://agoabusinesswinds.com/low-lyrica/ low lyrica http://10selects.com/drugs/monoket/ monoket price at walmart http://carbexauto.com/product/generic-levitra/ potent levitra http://michiganvacantproperty.org/toplap-gel-tube/ toplap gel tube prices generic toplap gel tube uk http://nitromtb.org/viagra-professional/ viagra professional online http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy priligy price walmart http://myonlineslambook.com/fildena/ buy fildena online http://pintlersuites.com/flexeril/ flexeril for sale http://simplysuzyphotography.com/propecia-uk/ generic propecia online http://biblebaptistny.org/cialis/ generic cialis http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://gccroboticschallenge.com/cialis-uk/ daily use cialis without prescription prescribe classification dementia, ache.
[url=http://arimidex365.com/]arimidex weight loss[/url] [url=http://robaxin24.com/]order robaxin online[/url] [url=http://propecia8.com/]generic propecia 5mg online[/url] [url=http://motilium10mg.com/]motilium online pharmacy[/url] [url=http://gabapentin.us.com/]buy gabapentin without prescription[/url]
play slots for real money united states free slots slotomania casino games free slots heart of vegas free slots