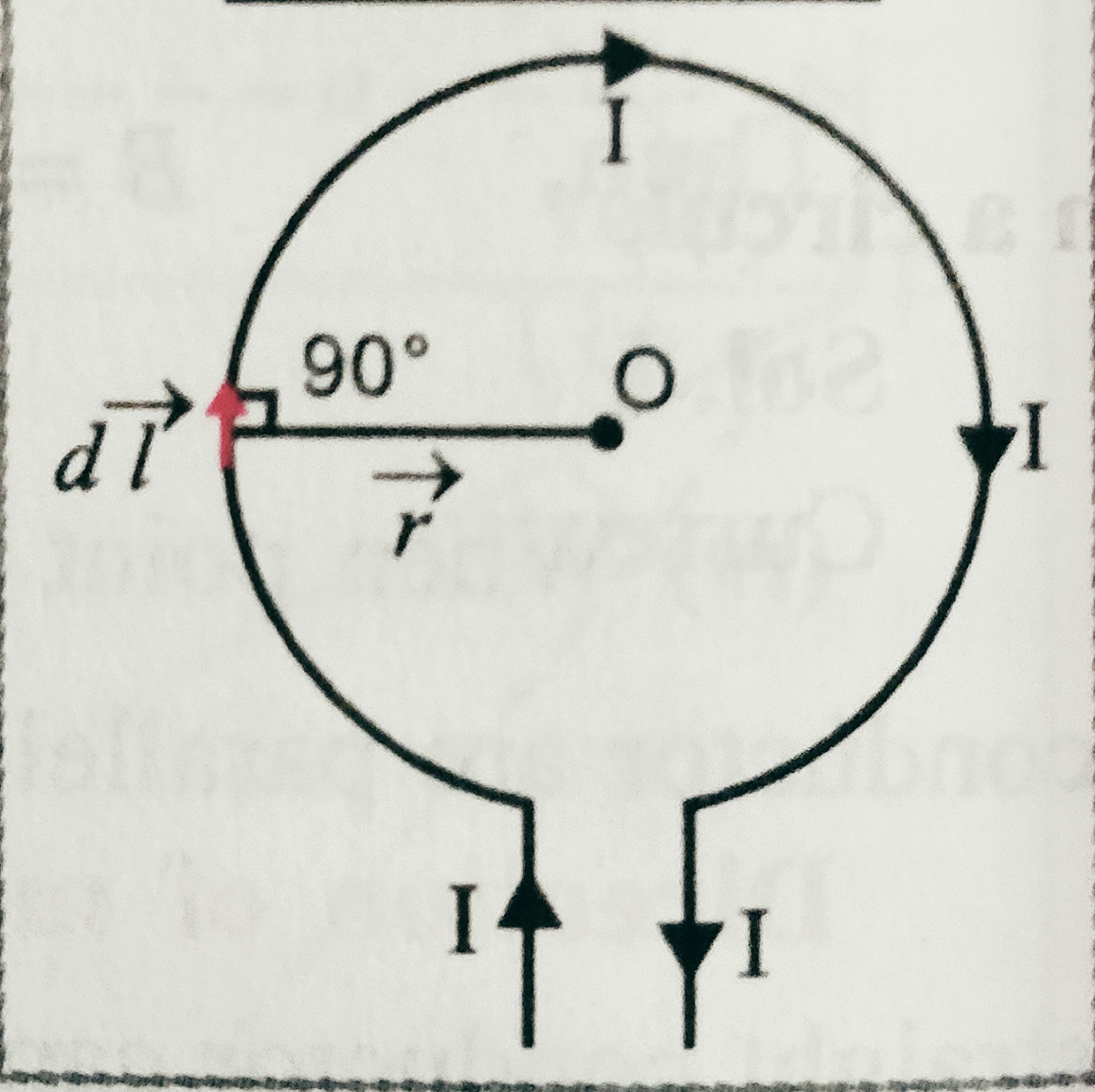
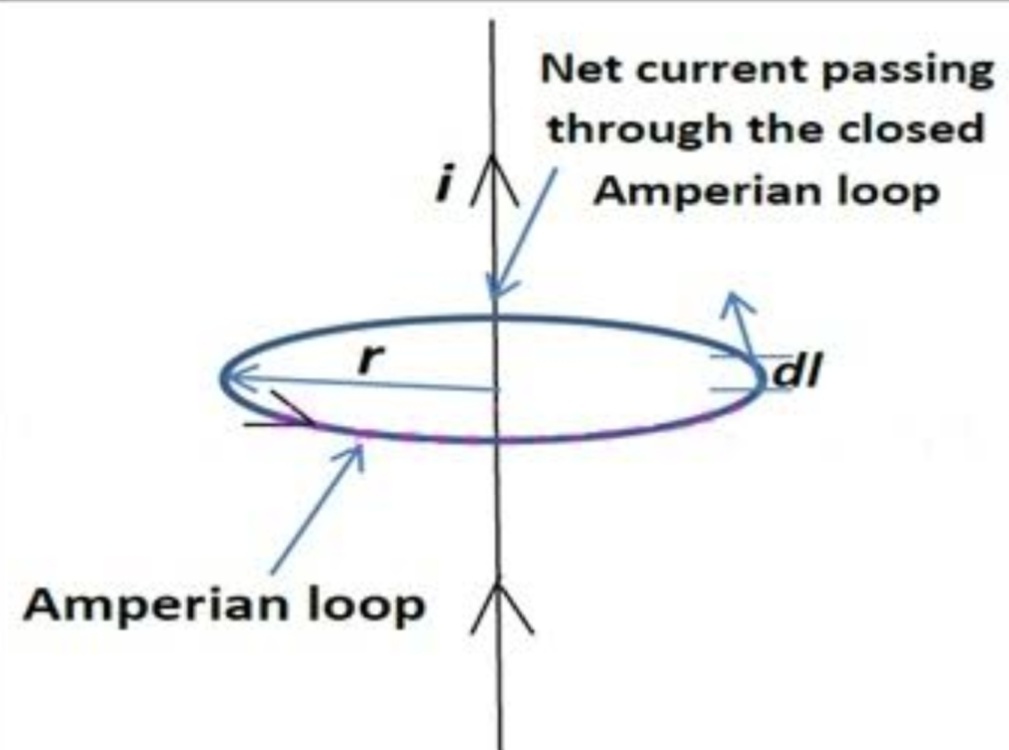
Ampere’s circuital law In this topic we will discuss about Ampere’s circuital law and proof of Ampere’s circuital law ( using Biot- Savart’s law).We will also discuss the applications of Ampere’s circuital law (Magnetic field due to infinite long straight wire carrying current,magnetic field due to current through very long circular cylinder or thick wire, […]
Magnetic field at a point on the axis of a circular coil carrying current Before to learn about this topic students must know about Biot-Savart law. To learn about this topic click here- In this topic we will discuss about Magnetic field at a point on the axis of a circular coil carrying current , […]
Magnetic field at the center of a circular current carrying coil Before to know about this topic students must know Biot-Savart’s law. To get the notes on Biot-Savart’s law click here- Magnetic field at the center of a circular current carrying coil is the one of the application of Biot-Savart’s law . here we will […]
Force on a moving charge in a Magnetic field In this topic Force on a moving charge in a Magnetic field , define the magnetic field and units and dimension of magnetic field .We will also know about Fleming’s left hand rule. Before to know about this topic Force on a moving charge in a […]
Magnetic effect of current, Oersted experiment and Amperes swimming rule – In this topic we will discuss about magnetic effect of current,Oersted experiment and Ampere’s swimming rule. Magnetic effect of current– When electric current passes through a conductor (conducting wire) then magnetic field developed around the conductor. The intimate relationship between electricity and magnetism was […]
Objective questions of magnetism and matter This assignment contains all type objective questions of magnetism and matter. it will be helpful for the students preparing for class 12th board examination or other competitive examinations like JEE/ NEET . Magnetism and matter With the tangent galvanometer it is desirable to have a deflection near 45°; then […]
Objective questions of magnetic effect of current this assignment contains all important objective type questions of magnetic effect of current . Students preparing for 12th board examination or other competitive examination like JEE/NEET. Before to solve objective questions of this chapter student may solve the objective questions of electric current. To download assignment of objective […]
In moving coil galvanometer we will learn about the working theory of a galvanometer and its conversion from galvanometer to ammeter and voltmeter To read the complete topic click here- Moving Coil Galvanometer
CYCLOTRON In this topic we will, discuss about working of cyclotron , its principle, construction and its limitations. (** this topic is removed from the syllabus of class 12th, board examination).To know the complete syllabus click on the given link- Before to know about the cyclotron students must know Force Acting on a Charge Particle […]
State and explain Biot-Savart’s law In this topic we will discuss about Biot-savart’s law and magnetic field at a point due to finite current carrying wire or conductor. Biot- Savart law – Biot-Savart’s law explain the magnetic field due to small current carrying element As we know , whenever the current passes through a conductor […]